Пусть прямая задача (2.16) имеет решение Х*. Тогда двойственная задача (2.17) также имеет решение У*, причем значения задач совпадают: <c,X*>=<b,Y*>. Равенство <c,X*>=<b,Y*> называют соотношением двойственности.
Отметим, что для несимметричной двойственной пары (2.18), (2.19) справедливы утверждения лемм 1,2,3:
1) для любой пары допустимых планов (Х,У) имеет место неравенство <c,X> ≤ <b,Y>;
2) если <c,X>=<b,Y>, то Х, У – оптимальные планы задач (2.18), (2.19);
3) если двойственная пара (2.18), (2.19) имеет допустимые планы Х, У, то задачи (3), (4) имеют решения Х*, У*.
Соответствующие доказательства полностью аналогичны предыдущим.
Из теоремы 1 и утверждения 2 выделим следующий результат:
Для оптимальности допустимых планов Х, У в двойственной паре (2.18), (2.19) необходимо и достаточно, чтобы <c,X>=<b,Y>.
Представим это равенство в другой форме, использующей ограничения задач (2.18), (2.19).
Поскольку b=AX, то <b,y>- <c,X> = <х, АТу> - <c,X> = <АТ -с,х>.
Следовательно, соотношение
<АТ-с,х>=0 (2.20)
есть необходимое и достаточное условие оптимальности допустимых планов х, в двойственной паре (3), (4).
(<a j, y>- cj)хj =0, j=1,……,n(2.21)
Таким образом, условие (2.20) эквивалентно системе равенств (2.21), которые характеризуют взаимосвязь ограничений двойственной задачи (2.19) и условий неотрицательности прямой задачи (2.18).
Эта взаимосвязь состоит в следующем: для оптимальности допустимых планов (Х, У) в двойственной паре (2.18), (2.19) необходимо и достаточно выполнение соотношений (условия равновесия):
1) если хj>0, то <a j, y>- cj =0;
2) если <a j, y>- cj >0, то хj =0.
Полученные условия могут быть использованы для построения оптимального плана одной из задач двойственной пары по известному решению другой (условие 1) фактически применялось в начале данного пункта для нахождения оптимального двойственного плана Y*).
Условия равновесия в симметричной паре. Экономическая интерпретация.
Вернемся к изучению симметричной двойственной пары задач линейного программирования
<c,X>→мах, AX ≤ b, X ≥ 0 (2.22)
<b,Y>→min, ATY ≥ c, Y ≥0 (2.23)
Докажем аналог теоремы 1 в этой ситуации.
Теорема 2. Пусть прямая задача (2.22) имеет решение Х*. Тогда двойственная задача (2.23) также имеет решение У*, причем значения задач совпадают: <c,X*>=<b,Y*>.
Доказательство: представим задачу (2.22) в канонической форме:
<c,X>→мах,
Ах + Х`=b,
X≥0, X`≥0,(2.22¢)
где Х ` = (хn+1,……,xn+m) – вектор дополнительных переменных.
В данной запаси план задачи, есть вектор (Х, Х`)ÎRn+m, целевой вектор имеет вид (с, 0), матрица условий – (АЕ), где Е – (m x m) единичная матрица. Основным переменным х1,……, хn соответствуют векторы условий а1,…….,аn (столбцы матрицы А), дополнительным переменным хn+1,…,xn+m – векторы условий е1,…..,еm (столбцы матрицы Е – единичные орты из Rm).
Запишем двойственную задачу для (2.22`)
<b,y>→min,
<aj,y> ³ cj, j=1,..,n,
<ei,y> ³ 0, i=1,…..m.
Понятно, что <ei,y> = yj. В векторно-матричной записи задача имеет вид: <b,y>→min,
ATy ≥ c, y ≥ 0,
т. е. совпадает с двойственной задачей (2.23).
Таким образом, задачи (2.22`), (2.23) образуют несимметричную двойственную пару, для которой справедлива теорема 1. Остается заметить, что значения задач (2.22), (2.22`) совпадают. Теорема доказана.
В совокупности с леммой 2 заключаем, как и ранее, что равенство <c,X>=<b,Y> является необходимым и достаточным условием оптимальности допустимых планов Х, Y в симметричной двойственной паре (2.22), (2.23).
На экономическом языке этот результат можно интерпретировать следующим образом: допустимый план производства Х и допустимый вектор оценок ресурсов Y являются оптимальными в задачах (2.22), (2.23) в том и только в том случае, если прибыль от реализации плана Х равна стоимости (в ценах у) необходимых ресурсов. Добавим, что при неоптимальном плане производства Х¹Х* для любого допустимого вектора оценок Y выполняется строгое неравенство <c,X> < <b,Y>, т.е. прибыль от реализации продукции меньше стоимости (ценности) необходимых ресурсов.
Докажем основной результат этого пункта.
Теорема 3. (равновесия). Доказательство в [5]. Для оптимальности допустимых планов Х, Y в двойственной паре (2.22), (2.23) необходимо и достаточно, чтобы
<AX - b,y>= 0, <АТу - с,х>= 0(2.24)
Доказательство: Представим задачу (2.22) в канонической форме (2.22`) и рассмотрим несимметричную двойственную пару (2.22`), (2.23). Применяя здесь условия равновесия, получаем:
<АТY -с,X>= 0,
<Y,X`>=0.
Замечая, что х`= b-AX, приходим к условиям (2.24). Теорема доказана.
Представим условия (2.24) в эквивалентной координатной форме.
Пусть āi = (ai1,ai2,…….ain) – i -тая строка матрицы А, i=1,…..m. Тогда основные ограничения прямой задачи (2.22) можно записать в виде:
<āi,X> ≤ bi, i=1,….,m.
Поскольку <āi,X >-bi ≤ 0, уi ≥ 0,
то должно быть (<āi,X>- bi) уi=0, i=1,….,m.
Аналогично обрабатывается второе равенство из (2.24) (см. переход от (2.18) к (2.19)).
В результате условия (2.24) представляются в эквивалентной координатной форме
(<āi,X>- bi) уi =0, i=1,….,m;
(<aj,Y> - cj) xj = 0, j=1,……n.
Отсюда получаем набор соотношений (условий равновесия), характеризующих оптимальные планы (х,у) в двойственной паре (2.22), (2.23):
если <āi,X>- bi < 0, то уi =0;
если уi > 0, то <āi,X>-bi =0;
если <a j, y>- cj > 0, то хj =0;
если хj > 0, то <a j, y>- cj = 0.
Дадим экономическую интерпретацию этим условиям в рамках задачи оптимального планирования производства (см. п. 1). Пусть, как обычно, (Х*,Y*) – решение двойственной пары (2.18), (2.17), т.е. х* = (х*1,……х*n) – оптимальный план выпуска продукции (х*j – количество продукта Р j, j=1,..n), у*=(у*1,…..y*m) – оптимальный вектор двойственных оценок используемых ресурсов (y* j – оценка (ценность) ресурса R i, i =1,….m).
Будем говорить, что ресурс R i дефицитен (не дефицитен), если
<āi,X*> = bi (<āi,X*> < bi).
Иными словами, ресурс R i дефицитен, если при оптимальном плане производства он используется в полном качестве. Тогда условия равновесия допускают следующее толкование (для х=х*, у=у*):
1. Если ресурс Ri не дефицитен, то его двойственная оценка равна нулю;
2. Если ресурс Ri имеет положительную двойственную оценку, то он является дефицитным;
3. Если оценка расхода ресурсов на единицу продукта Рj больше соответствующей прибыли от реализации, то продукт Рj при оптимальном планировании не производится;
4. Если продукт Рj по оптимальному плану выпускается, то оценка расхода ресурсов на его производство равна прибыли от реализации.
На основании свойств 1), 2) заключаем, что двойственные оценки могут служить характеристикой дефицитности ресурсов. Свойства 3), 4) характеризуют структуру оптимального плана – какие продукты производятся (не производятся) и почему.
Пример 2. 12. 5.
На станках трех видов С1, С2, С3 последовательно обрабатываются детали четырех видов: D1, D2, D3, D4. Известно, сколько часов каждая деталь изготавливается на каждом станке, сколько времени может отработать каждый станок и какая прибыль может быть получена при продаже одной детали каждого вида (табл. 43).
Таблица 43
| Станки | Сколько требуется часов работы станка для выпуска одной детали | Фонд времени станка | |||
| D1 | D2 | D3 | D4 | ||
| C1 | 2 | 4 | 0 | 8 | 12 |
| C2 | 7 | 2 | 2 | 6 | 8 |
| C3 | 5 | 8 | 4 | 3 | 48 |
| Прибыль за 1 деталь | 3 | 4 | 3 | 1 | - |
Проверить, будет ли план, предусматривающий выпуск трех деталей второго вида и одной детали третьего вида оптимальным по критерию "максимум прибыли".
Математическая модель задачи:
Обозначим через х,j - объем выпуска деталей j -го вида (j =1,..,4) и запишем математическую модель задачи:
f =3×х1 + 4×х2 + 3×хз + х4® max;
2×х1 +4×х2 +8×х4 ≤ 12 (1)
7×х1 + 2×х2 + 2×х3 +6×х4≤ 8 (2)
5х1 + 8×х2 +4×х3 +3×х4 ≤ 48 (3)
хj ≥ 0, j= 1,...,4.
Понятно, что ответить на поставленный вопрос можно решив приведенную ЗЛП симплекс-методом. Приведем решение с помощью теорем двойственности. Проверим, является ли вектор Х (0, 3, 1, 0) планом:
2×0 +4×3+8×0 = 12
7×0 +2×3+2×1+6×0 = 8
5×0 +8×3+4×1+3×0 = 28 < 48.
Значение целевой функции на этом плане равно
f = 3×0 + 4×3 + + 3×1 + 1×0 = 15.
Двойственная задача имеет вид:
W=12×y1 + 8×y2+ 48×y3® min
2×y1+7×y2+5×у3 ≥ 3 (1)
4×y1+2×y2+8×y3 ≥ 4 (2)
2×y2+4×y3 ≥ 3 (3)
8×y1+6×y2+3×y3 ≥ 1 (4)
y1,2,3 ≥ 0.
Для нахождения оценок у1, y2, y3 используем вторую теорему двойственности. Поскольку ограничение (3) прямой задачи выполняется как строгое неравенство, то у3 = 0. Так как х2 > 0 и х3 > 0, то ограничения (2) и (3) двойственной задачи, связанные с этими переменными, будут выполняться как равенства:
4×y1+2×y2+8×y3-4=0 (2)
2×y2+4×y3 -3 = 0 (3)
Итак, для получения определенных оценок имеем систему линейных уравнений:
y3=0
4×y1+2×y2+8×y3=4
2×y2+4×y3=3
т.е. y1 =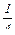 
, у2= 
, у3= 0.
Вычислим значение целевой функции двойственной задачи:
W (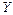
)= 12× 
+8× 
+48× 0 = 15, т.е. f = W (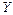)= 15.
По первой теореме двойственности предложенный план Х (0,3,1,0) является оптимальным.
Экономико-математический анализ решений базируется на свойствах двойственных оценок. В пределах устойчивости двойственных оценок имеют место следующие свойства:
1. Величина двойственной оценки того или иного ресурса показывает, насколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на одну единицу (двойственные оценки измеряют эффективность малых приращений объемов ресурсов в конкретных условиях данной задачи).
В примере 2.12.5 увеличение фонда времени работы станка С1 на 1 час привело бы к росту максимальной суммы прибыли на 0,25 (y1 = 1/4), а увеличение фонда рабочего времени этого станка не повлияет на оптимальный план выпуска продукции и сумму прибыли.
Указанное позволяет выявить направления "расшивки" узких мест, обеспечивающие получение наибольшего экономического эффекта, а также целесообразность изменения в структуре выпуска продукции с позиций общего оптимума.
2. Двойственные оценки отражают сравнительную дефицитность различных видов ресурсов в отношении принятого в задаче показателя эффективности. Оценки показывают, какие ресурсы являются более дефицитными (они будут иметь самые высокие оценки), какие менее дефицитными и какие совсем недефицитны (избыточны).
В примере 2.12.5 недефицитным ресурсом является фонд рабочего времени станка С3 поскольку у3 = 0.
Острее ощущается дефицитность ресурса С2 (у2= 3/2) — он более дефицитен, чем ресурс С1 (y1 = 1/4).
3. Двойственные оценки позволяют определять своеобразные "нормы заменяемости ресурсов": имеется в виду не абсолютная заменяемость ресурсов, а относительная, т. е. заменяемость с точки зрения конечного эффекта и лишь в конкретных условиях данной задачи.
В нашем примере относительная заменяемость ресурсов определяется соотношением (нормой) 
4. Двойственные оценки служат инструментом определения эффективности отдельных хозяйственных решений (технических способов), с их помощью можно определять выгодность новых изделий, эффективность новых технологических способов: если Δj> 0 — невыгодно.
В примере 2.12.5 следует решить вопрос о целесообразности включения в программу производство деталей при затратах ресурсов станков: 8, 2 и 3 соответственно и ожидаемой прибыли в: а) 6 ед; б) 1 ед.
В случае а) 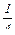×8 + ×2 + 3×0 - 6=-1<0— выгодно.
В случае б) ×8 + ×2 + 3×0 -1=4>0 — невыгодно.
При решении практических задач нередко приходится иметь дело не с общей задачей, а со специальными видами задач, порожденными отдельными классами экономических моделей. Для поиска оптимальных решений в этих моделях в ряде случаев могут использоваться и общие методы, однако, как правило, более выгодно при решении этих задач учитывать их специфику.
Пример 2. 12. 6.
Прямая задача: f =5×x1+6×x2+x3+x4® min
x1+3×x2-x3+x4³ 18
3×x1+2×x3-4×x4³ 24 xi³0
Двойственная задача: W=18y1+24y2®max
x1: y1+3×y2£ 5 (1)
x2: 3×y1£ 6 (2)
x3: -y1+2×y2£ 1 (3)
x4: y1- 4y2 £1 (4)
yi³0
Рис. 26.
точка C y2* = 
= 
;
y1* =2
mах W=W(C)
mах W(y*)=18× 2+24× = 52
так как (3) и (4) ограничения выполняются при оптимальном плане y*(2, ) как неравенства (они не проходят через т. С), то по условиям равновесия х3=х4=0, так как y1* ≠ 0; y2* ≠ 0, то ограничения прямой задачи будут выполняться как равенства.
f=5×x1+6×x2® min
x1+3×x2=18 Þ x2*=2
3×x1=24 Þ x1*=8
xi³ 0
min f (х*)=5× 8+6× 2=52
min f (х*)= mах W(y*)
Значения задач совпадают, значит оба плана оптимальны.
Пример 2.12.7: Диспетчерская служба имеет следующие минимальные потребности в количестве диспетчеров в различное время суток:
Таблица 44
| Порядковый номер периода | Время суток (час) | Минимальная потребность в диспетчерах |
| 2 - 6 | ||
| 6 - 10 | ||
| 10 - 14 | ||
| 14 - 18 | ||
| 18 - 22 | ||
| 22 -2 |
При этом период 1 следует сразу же за периодом 6. Каждый диспетчер ежедневно приступает к работе в начале соответствующего периода и работает 8 часов без перерыва. Требуется определить число диспетчеров, выходящих на работу в каждом периоде суток, с тем, чтобы обойтись при этом минимальным числом работников.
Решение.
Обозначим:
xj - число диспетчеров, приступающих к работе в j-ый период (j =1,..,6).
Прямая задача
при ограничениях:
х1 + х6 ≥ 20; ← y1
х1 + х2 ≥ 50; ← y2
х2 + х3 ≥ 80; ← y3
х3 + х4 ≥ 100; ← y4
х4 + х5 ≥ 40; ← y5
х5 + х6 ≥ 30; ← y6
х j ≥ 0; j = 1,...,6
Двойственная задача.
W(y) = 20 y1 + 50 y2 + 80 y3+ 100 y4 + 40 y5 + 30y6 → max.
y1 + y2 ≤ 1;
y2+ y3 ≤ 1;
y3 + y4≤ 1;
y4 + y5 ≤ 1;
y5 + y6 ≤ 1;
y6 + y1 ≤ 1;
y i = 0, если в i-период диспетчеры не выходят
1, если в i-период диспетчеры приступают к работе
i =1,...,6.
т.к. коэффициент при y4 самый большой, равный 100, то положим, что y4=1, тогда y3 = 0, y2 = 1, y1 = 0, y6= 1, y4 = 1, y5 = 1, т.е. y (0,1, 0, 1, 0, 1).
Тогда целевая функция двойственной задачи равна: W(y) = 180.
По условиям равновесия (второй теореме двойственности) оптимальный план прямой задачи будет удовлетворять условиям:
|
|
х*1 + х*2 = 50; х*1 + х*6 ≥ 20;
х*3 + х*4 = 100; х*4 + х*5 ≥ 40;
х*5 + х*6 = 30; х*2 + х*3 ≥ 80;
х j ≥ 0; j = 1,...,6
Из (1) следует, что х*1 + х*2 + х*3 + х*4 + х*5 + х*6 = 180 = f (x*) = W(y*). Значит, любой целочисленный план х*, удовлетворяющий системам уравнений (1) и (2) является решением задачи. Например:
х* (0, 50, 60, 40, 10, 20);
или
х* (0, 50, 30, 70, 0, 30);
f (x*) =180.
или
х* (50, 0, 80, 20, 20, 10);
Контрольные вопросы
1) Какая переменная вводится в базис при поиске минимума функции?
2) К чему приводит увеличение числа ограничений?
3) В каких случаях получается бесконечное множество решений?
4) К чему приводит исключение из модели неактивных ограничений?
5) Какое ограничение можно заменить двумя неравенствами?
6) Как определить по симплекс – таблице, что поставленная задача не имеет решений?
7) Какие методы используются в случае наличия ограничений в виде равенства или неравенства больше или равно?
8) В каких случаях задача линейного программирования имеет множество альтернативных решений?
9) В каких случаях следует решать двойственную задачу линейного программирования?
10) Как определить отсутствие решений в двухэтапном методе и методе больших штрафов?
11) На что влияет изменение запасов ресурсов?
12) В каких случаях используется двойственный симплекс - метод?
13) С какой целью рассчитывается отношение в симплекс-таблице?
14) Чем отличается двойственный симплекс метод от симплексного метода?
15)Как по симплекс-таблице определить, что ресурс является дефицитным?
Список литературы
1. Акулич Л.И., Капустин В.Ф. Математическое программирование в примерах и задачах. Учебн.пос. для студентов экономических специальностей-М.: Высш.шк., 1986 г.
2. Исследование операций в экономике: Учебн.пос./ Под ред. Н.Ш. Кремера-Банки и биржи, 1997 г.
3. Волков И.К.,. Загоруйко Е.А. Исследование операций. Учебник для вузов М.:Изд-во МГТУ, 2000 г.
4. Кузнецов Ю.Н., Кузубов В.И. Математическое программирование.-М.: Высш.шк., 1976.
5. Курицкий Б.Я. Оптимизация вокруг нас. - Л.: Машиностроение, 1989 г.
6. Таха Ч. Введение в исследование операций: Пер с англ.- М.: Мир, 1985 г.
7. Фомин Г.П. Математические методы и модели в коммерческой деятельности.- М.: Финансы и статистика, 2001 г.
8. Исследование операций. Том 1: Методологические основы и математические методы. Учебник./ Под ред. Дж. Моудера, С. Элмаграби. - М.: Мир, 1981 г.
9. Банди Б. Основы линейного программирования. Пер с англ.- М.: Радио и связь, 1989 г.
10. Интрилигатор М. Математические методы оптимизации и экономическая теория. Пер с англ.- М.: Айрис-пресс, 2002.
11. Кустова В.И. Математическое программирование. Сборник задач и упражнений. Части I, II и III- Иркутск: издательство – Иркутская экономическая акакдемия, 1996 г.
12. Срочко В.А. Основы линейного программирования. Учебное пособие. – ИИНХ - Иркутск. 1993, 62 с.
13. Хазанова Л.Э. Математическое моделирование в экономике. Учебное пособие – М.: Издательство БЕК,1998, 141 с
14. Исследование операций в экономике / Под ред. Н.Ш. Кемера - М.: Банки и биржи, ЮНИТИ, 1997 - 407 г.