Модель окисления Дила- Гроува

Рис.2.2. Диаграмма высокотемпера­турного окисления кремния

Первые попытки описания термического окисления кремния осно­вывались на известных моделях роста окисла на металлах, в которых предполагалось, что при высоких температурах процесс окисления является следствием диффузии заряженных частиц - ионов и электронов -через растушую пленку. При этом скорость химической реакции считалась много большей скорости диффузионного процесса.

Основной моделью роста окисла является модель Дила-Гроува (Д-Г), рассматривающая процесс окисления состоящим из двух этапов - массопереноса окислителя в растущем окисле и протекания химической реакции кремния с окислителем. Модель предполагает три потока (рис.2.2):

1) массоперенос окислителя через внешнюю границу растущего окислаSiO₂ из газовой фазы (потокF₁):

F = h(C * - C₀),

гдеh - коэффициент переноса окисляющих частиц через внешнюю границу окисла;C* и C₀ - концентрации окисляющих частиц вне окисла и вблизи

поверхности внутри окисла в любой момент времени окисленияt (C₀ принимается обычно равной предельной растворимости окислителя вSiO₂);

2)

диффузию окисляющих частиц через окисел к границе разделаSiO₂ -Si (потокF₂):

гдеD - коэффициент диффузии окисляющих частиц;C_i - концентрация окислителя на границеSiO₂ -Si;

3) химическую реакцию взаимодействия окислителя с кремнием (потокF₃):1

F3 = kC _i

где к - скорость реакции.

 

В условиях установившегося равновесия (поток F F = F₁ = F₂ = F₃) решается дифференциальное уравнение для скорости окисления:

гдеN - число частиц окислителя, необходимое для создания единицы объема окисла.

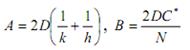Если ввести обозначения то уравнение (2.1) примет вид:

 

dx/dt=B/(A+2x).(2.2)

Кремний легко окисляется при комнатной температуре, так что его поверхность всегда покрыта слоем окисла толщиной от 2 до 8 нм. Кроме того, термическое окисление может проводиться многократно. Для исследуемого процесса следует иметь в виду, что приt = 0 на поверхности кремния уже мог быть слой окисла толщиной х₀. Поэтому интегрирование уравнения (2.2) ведется в пределах х₀ - х, и решение его имеет вид:

 

x² + Ax = B(t +1₀), где t₀ - время, (2.3)

 

где t₀ - время, соответствующее начальной толщине окисла х₀.

Рис.2.3. Зависимость толщины окисла кремния от времени

окисления при высокой температуре

Зависимость толщины окисла от времени окисления при высокой (от 700 до 1200 °С) температуре изображена на рис.2.3. При малых временах окисления t<<A²/4B рост окисла описывается линейным законом

при больших временах окисления t >> A² /4B - параболическим

x² = Bt ≡ k_pt, (2.5)

где k_l и k_p - константы линейного и параболического роста соответст­венно. Имеется некоторое характерное время t_ар, при превышении которого

линейный закон роста окисла переходит в параболический (см. рис.2.3). Уравнение (2.3) можно записать также в виде

x²/ B + (A / B) x = t (2.6)

(если t₀ << t, то t₀ можно не учитывать).

Поделив все части уравнения (2.6) на х и проведя небольшие пре­образования, получим:

x = B(t / x - A/B). (2.7)

Уравнение (2.7) есть уравнение прямой в координатах [х, t/x], которая отсекает на оси абсцисс отрезок, численно равный обратной величине линейной константы A / B = k_l, и имеет угол наклона, тангенс которого равен

параболической константе роста окисла B = k_p.

Модель Дила-Гроува описывает достаточно точно экспериментальные результаты в широком диапазоне температур и толщин окисла,, за исключением начального участка роста окисного слоя (особенно в сухом кислороде) толщиной примерно до 30 нм.

Окисление под давлением

Влияние парциального давления окислителя

Константа k_p в модели Д-Г линейно зависит от парциального давления окислителя, вследствие чего может быть использован закон Генри:

C = HPs,

где С - концентрация окислителя; Н - постоянная Генри; P_S - парциальное давление окислителя. Экспериментально показано, что в диапазоне температур 850 - 1000 °С при давлениях порядка 104 - 106 Па закон Генри соблюдается. Это свидетельствует о том, что диссоциация молекул окислителя на границе газ - SiO₂ отсутствует, следовательно, через окисел идет диффузия и сухого кислорода, и воды в молекулярной форме.

Для линейной константы зависимость от давления окислителя оказалась также линейной, только в узком диапазоне высоких температур (1000 - 1200 °С) и давлений (0,1 - 1,0)-10⁵ Па окислителя. Более точная зависимость может быть описана соотношением k ~ Pⁿ. Для окисления в сухом O₂, по данным различных экспериментов, показатель n меняется от 0,59 до 0,70 при температурах до 900 °С и от 0,8 до 1,0 при более высоких температурах. Кроме того, n зависит от ориентации подложки, что может быть связано с промежуточным этапом реакции O₂ с Si, хемосорбцией кислорода, а также участием в реакции, помимо молекулярного, и атомарного кислорода.

При окислении в парах воды или влажном кислороде (H ₂O + O₂) во всем диапазоне температур и давлений порядка 105 Па n = 1/2.