Основные положения теории скрытности

Прежде чем кратко изложить основные положения теории скрытности, представим структуру теории путем последовательного введения ее основных понятий.

Множество (Ω). Исходным понятием теории является понятие некоторого множества Х возможных достоверно непредсказуемых событий. Такими событиями в радиотехнике могут быть неисправность в аппаратуре, появление в «эфире» излучения на некоторой, до того неизвестной стороннему наблюдателю частоте. В криминалистике это множество может представлять систему версий.

Множество определяется всем мыслимым ассортиментом неисправностей или возможных степеней свободы (арсеналом частот) при выборе рабочей частоты для конкретной передачи. Для системы версий (Ω) множество представляет собой все возможные версии без исключения.

Обозначим множество событий буквой (название множества), ассортимент (арсенал) событий (мощность множества) – буквой , составляющие множество события условимся обозначать , где i – номер события в множестве (нумерация, естественно, произвольная), и запишем в виде .

Можно рассматривать в качестве случайных событий числа , при этом вместо множества событий будем иметь дело со случайной величиной , принимающей численные значения от 1до . Условно можно представить множество событий в форме геометрического образа (рис. 15). Каждый из квадратиков с точкой внутри представляет собой возможное событие ; некоторое де-факто возникшее (реализовавшееся) событие при i=r обведено кружком. Будем для краткости называть его реасобытием. Чаще прибегают к объемному представлению множества в трехмерном или многомерном пространстве.

Рис. 15. Схематическое изображение множества

(по З. М. Каневскому и В. П. Литвиненко, 1991)

Будем считать множество заданным, если кроме мощности известны вероятности всех его возможных реализаций , которые будем обозначать через 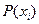или . Величина 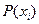, рассматриваемая как функция целочисленной переменной i, представляет собой закон распределения вероятностей множества . При несовместимых событиях имеет место равенство

, (1.1)

Поисковая процедура. Выявлять событие , которое в данной обстановке возникло в действительности (стало реасобытием), можно по-разному, например по очереди обследовать все квадраты (см. рис. 15) и остановиться на том, в котором обнаружено событие 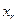(в кружке). Можно поступить иначе: сначала разделить множество на два подмножества: верхнее 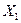и нижнее 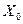– и попытаться установить по тем или иным признакам, в каком из них просматривается след события. Под следом понимается тот или иной признак его присутствия в подмножестве 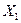или 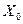. Например, избыточная (над шумами) мощность или энергия сигналов в одном из частотных поддиапазонов 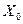или 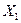, на которые настроены приемники. Если след обнаружен в верхнем подмножестве, он в свою очередь разбивается на два других подмножества и 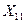и т.д. Деление продолжается до тех пор, пока не будет достигнуто подмножество только с одним искомым событием в нем.

При обращении к рис. 15 наш глаз и управляющий им «аппарат» (мозг) осуществляют определенную, отнюдь не мгновенную поисковую процедуру до того, как обнаружит клетки с кружком.

Множество мощностью допускает многократное деление на равные по мощности подмножества. Число квадратов в нем равно 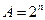, где n=4 – целое число. Такие множества будем называть симметричными.

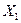Дерево поиска. Описанную поисковую процедуру удобно иллюстрировать посредством дерева поиска. Изображать его будем корнем вверх и строить следующим образом. Верхний, корневой, узел обозначим буквой , относящейся к названию множества. От него поведем две ветви к подмножествам и 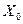, от каждого из них отведем по две ветви к подмножествам , , 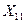и 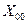, и т.д. Тупиковые узлы(на чертеже их восемь) будем называть концевыми, или финальными. Вырожденные в них подмножества содержат по одному , ,каждое, так что можно написать 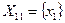, 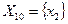и т.д. Нумерация событий на чертеже – слева направо. По достижении финального узла сверху вниз поиск заканчивается – событие установлено.

Для упрощения записи концевые узлы обозначены просто соответствующими им пронумерованными событиями , .

Равенство означает, что дерево отражает один из возможных алгоритмов поиска .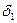

Типичной в описанном смысле является хорошо известная процедура сравнительного взвешивания монет, разделяемых на горстки для выявления фальшивой, отличающейся по весу. Недостаточный или избыточный вес одной или другой горстки монет служит при этом следом: к какой из горсток обратиться для дальнейшего поиска.

Решения о направлении поиска, принимаемые в узлах дерева кромеконцевых, осуществляются посредством операций, которые будем называть двоичными измерениями (диз). Относительно той или иной фиксируемой ветви при двухальтернативном выборе двоичное измерение дает ответ ДА или НЕТ.

Дерево поиска "сродни" кодовому дереву, используемому в теории информации.

Мера скрытности. Введем понятие длины пути от корня дерева к некоторому его концевому узлу . Длина пути определяется числом ветвей отделяющих начальную точку маршрута от конечной. Перемещению по данной ветви сопутствует одно предварительное двоичное измерение. В связи с этим длину пути можно выражать в дизах.

Примем в качестве меры скрытности 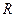множества возможных событий 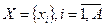, среднее значение (его математическое ожидание ), вычисляемое с учетом вероятностей использования различных путей в процессе раскрытия реасобытия:

, (1.2)

Число путей в частном случае (отсутствие помех и ошибок намерений) совпадает с числом возможных событий .

Мы будем употреблять выражение скрытность события , имея, однако, в виду, что она определяется всем множеством событий с его вероятностными характеристиками. Одно заранее известное детерминированное событие 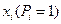скрытностью не обладает.

Виды скрытности. В зависимости от того, что является предметом поиска, его целью можно говорить о различных видах скрытности. В частности, применительно к радиосигналам можно выделить частотную скрытность, если поиск ведется в целях выявления радиопередачи в дискретной сетке частот. Структурная скрытность возникает при анализе структуры сигналов, например широкополосных и образующих их кодовых комбинаций из заданного арсенала. При неопределенном местоположении радиостанции появляется пространственная скрытность, что особенно существенно для подвижных объектов. Временная скрытность имеет место для прерывистых или спорадических радиопередач, когда неопределенными оказываются время начала работы, продолжительность сеанса связи и интервалы времени между очередными сеансами.

Различные виды скрытности связаны между собой в том смысле, что временная скрытность (короткое время передачи), например, может затруднить определение других ее данных. Отсутствие сведений о поляризации волны затрудняет определение несущей частоты и т.д. В связи с этим уместно говорить о комбинированных видах скрытности – частотно-временной и других.

Характеризуя скрытность сигналов, обычно оговаривают условия, в которых производится их прием (при действии шумов или маскирующих помехах и т.д.).

Неотъемлемыми условиями раскрытия сигналов являются их достаточные для анализа мощность или энергия, которые в целях обеспечения скрытности стремятся уменьшить до предела. В связи с этим говорят об энергетической скрытности сигналов, которая, как и другие виды скрытности, может оцениваться количественно.

Применительно к задаче локализации неисправности в аппаратуре или патологии в некотором биологическом объекте уместно говорить о диагностической скрытности объекта.

Цена диза. Двоичные измерения на разных этапах поиска часто требуют затрат времени, труда, осуществления вспомогательных операций, риска. С учетом этого введем для оценки скрытности понятие цены диза.

Возвратимся к дереву поиска (см. 1.4) и пронумеруем в произвольном порядке все его ветви от 1до n, где n – полное число ветвей дерева. Нетрудно показать, что

, (1.3)

где А – мощность множества. Длину i -го пути по дереву в дизах можно записать в виде

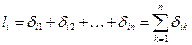, (1.4)

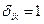где принимает значения ,если k -я ветвь входит в состав i -го пути, и 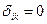, если не входит. Пусть представляет собой множитель, равный или больший единицы, учитывающий относительную стоимость (в смысле трудоемкости, затрат времени, риска) k -го двоичного измерения на i -м пути. Обозначим с учетом значений длину i -го пути через и представим ее в виде

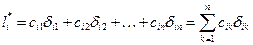, (1.5)