В случае криволинейных границ амплитуда отраженных волн на временном разрезе, до применения миграции, подвержена влиянию геометрической фокусировки или расфокусировки лучей за счет кривизны границы. Форма структуры может быть описана радиусом кривизны или обратной величиной – кривизной. При этом нулевая кривизна соответствует плоской границе, а бесконечная кривизна – точке дифракции. На (Рисунок 11, а) показаны конусы энергии, отраженной от неплоской границы. Энергия, отраженная от антиклинали, распределяется по большей площади поверхности наблюдения, чем для синклинали, следовательно, над синклиналями наблюдаются более сильные отражения, а над антиклиналями – более слабые.
Особое значение имеет соотношение между глубиной границы и ее радиусом кривизны. В зависимости от этого соотношения лучи отраженной волны могут сходиться, быть параллельными или пересекаться. (Рисунок 11, б) Пока лучи не пересекаются, амплитуда отраженной волны больше амплитуды волны, отраженной от плоской границы. В случае пересечения лучей будет наблюдаться сложная интерференционная картина. (Шалаева, Старовойтов, 2010)
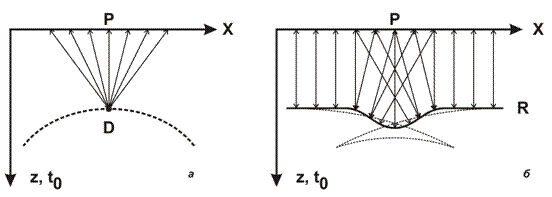
Рисунок 11: Схематическое изображение расфокусировки (а) и фокусировки (б) лучей над антиклинальной структурами (Шерифф, Гелдарт, 1987)
Hilterman (1975, 2001) обобщил приблизительные количественные оценки амплитудных и фазовых изменений сигнала при отражении от антиклинальных и синклинальных структур. Скаляр и фаза, вызываемые геометрическими формами, представлены в (Таблице 1).
| Геометрия | Скаляр | Фаза | ||
| 2Д |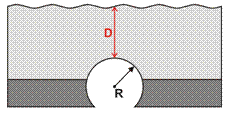 
| Антиклиналь |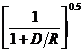 
Уменьшение
| |
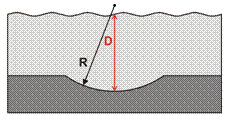
| Пологая синклиналь |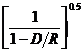 
Увеличение
| ||
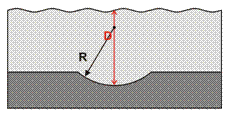
| Синклиналь |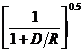
Увеличение
| 90° | |
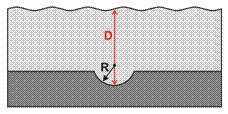
| Крутая синклиналь |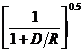
Уменьшение
| 90° | |
| 3Д | Скаляр 3Д = Скаляр падение * Скаляр простирание Фаза 3Д = Фаза падение + Фаза простирание |
Таблица 1: Скаляр и фаза для отражений от антиклинали и синклинали
Приведенные формулы действительны для двумерного случая, то есть считается, что профиль пересекает бесконечную структуру вкрест простирания. В случае трехмерных структур, амплитуды отражений от них описываются приближенно как произведение вышеперечисленных множителей по простиранию и вкрест него.
В статье (Lindsey, 1989) рассматривается изменение формы зон Френеля в случае изометричных в плане антиклиналей или синклиналей. Важнейшим параметром (К) является отношение глубины до отражающей границы к радиусу кривизны синклинали или антиклинали. Для антиклинали зоны Френеля будут меньше, по сравнению со случаем плоской границы, в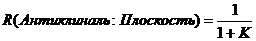 
раз. Для синклиналей зоны Френеля увеличатся в 
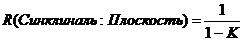раз. Для синклинали максимум К равен единице. Этот предел достигается в случае полной фокусировки, когда глубина и радиус кривизны одинаковы. Для синклиналей размер зон Френеля увеличивается более значительно, по сравнению с ожидаемыми эффектами от антиклиналей. (Lindsey, 1989).