Оглавление
Введение. 3
Глава 1. Определение понятий вертикальной и горизонтальной разрешающей способности сейсмоакустических исследований. 4
Разрешающая способность по вертикали. 4
Разрешающая способность по горизонтали. 9
Пространственная разрешающая способность при многоканальных наблюдениях. 12
Зоны Френеля для широкополосных сигналов. 13
Влияние геометрии отражающей границы.. 16
Математические оценки горизонтальной разрешающей способности. 18
Разрешающая способность после миграции. 21
Глава 2. Геолого-геофизическая характеристика района работ. 23
Особенности геологического строения региона. 24
Четвертичные отложения. 26
История развития и характерные типы отложений. 29
Глава 3. Многоканальные сейсмоакустические наблюдения по методике ОГТ. 33
Аппаратура. 33
Методика. 38
Обработка. 40
Характеристика исходных данных. 41
Расчет геометрии наблюдений и бинирование. 43
Предварительная обработка. 44
Деконволюция. 45
Ввод кинематических поправок и суммирование по ОГТ. 49
Миграция. 51
Глава 4. Оценка вертикальной разрешающей способности. 53
Глава 5. Оценка горизонтальной разрешающей способности. 58
Выводы и рекомендации. 63
Список литературы.. 64
Введение
Работа посвящена анализу вертикальной и горизонтальной разрешающей способности сейсмоакустических методов на мелководных акваториях по результатам многоканальных наблюдений по методике ОГТ на примере данных, полученных в губе Ругозерской Кандалакшского залива Белого моря, а также на основе данных волнового моделирования.
В настоящее время существуют различные подходы к оценке разрешающей способности сейсмоакустических методов. В целом, под разрешающей способностью понимается то минимальное различие между двумя объектами, при котором можно утверждать, что объектов два, а не один. Принятые оценки вертикальной разрешающей способности основаны на разделении отражений от кровли и подошвы слоя, и связаны с длительностью импульса. В то время как оценки горизонтальной разрешающей способности основываются на понятии зон Френеля. Однако, для импульсов сложной формы, широкополосных сигналов, с учетом возможностей деконволюции и миграции, разрешающая способность метода становится не столь очевидной.
|
|
Работа была посвящена решению следующих задач:
· Анализу литературы и определению понятий вертикальной и горизонтальной разрешающей способности сейсмоакустических исследований,
· Получению кондиционных полевых данных многоканальных наблюдений в губе Ругозерской Кандалакшского залива Белого моря,
· Математической обработке данных полевых наблюдений,
· Моделированию волновых полей,
· Оценка вертикальной разрешающей способности,
· Оценка горизонтальной разрешающей способности.
Полевые материалы были получены при участии автора в течение двух полевых сезонов 2009-2010 года в рамках морской междисциплинарной учебной практики на Беломорской биостанции МГУ. Обработка данных выполнялась в программе RadExPro Plus Advanced 2011, моделирование волновых полей производилось в программе Tesseral Pro.
Глава 1. Определение понятий вертикальной и горизонтальной разрешающей способности сейсмоакустических исследований
С самого начала своего развития, сейсмоакустические исследования, в отличие от традиционных методов сейсмической разведки, рассматривались как высокоразрешающие методы. Это связано, в первую очередь, с применением их на небольших глубинах с использованием высокочастотных импульсных источников.
|
|
В настоящее время в литературе описаны несколько различных подходов к определению понятий вертикальной и горизонтальной разрешающей способности сейсмических и в частности, сейсмоакустических исследований. Далее рассмотрены некоторые из этих подходов.
Традиционно, в сейсморазведке вертикальная разрешающая способность определяет то минимальное различие между двумя объектами, при котором можно утверждать, что имеется не один объект, а два объекта. Применительно к сейсмическим волнам можно говорить о том, 1) как далеко (в пространстве и времени) должны отстоять две поверхности, чтобы их можно было выделить как две самостоятельные отражающие границы, и 2) насколько две структуры, относящиеся к одной поверхности раздела, должны быть разделены в пространстве, чтобы проявиться как отдельные морфологические образования (Шериф, 1987).
Разрешающая способность по вертикали
В случае использования импульсов малой длительности, не возникало бы проблем разрешения двух близкорасположенных отражений. В реальности сейсмоакустические импульсы содержат ограниченный диапазон частот и поэтому имеют значительную длительность.
Таким образом, под величиной вертикальной разрешающей способности обычно понимают минимальную временную мощность tp при которой волны, отраженные от его кровли и подошвы, удается идентифицировать отдельно друг от друга, т.е. tp=2τи, где τи – длительность зондирующего импульса f(t). Исходя из этого положения, повышение разрешающей способности связано только с сокращением величины τи. (Калинин, Кульницкий, Токарев, 1992).
|
|
Рэлей определил предел разрешения условием, при котором два колебания запаздывают относительно друг друга на полупериод, и, следовательно, интерференционные явления максимальны, причем интерференция может приводить как к усилению, так и к ослаблению суммарного эффекта (Шериф, 1987). По Рэлею минимальная мощность слоя, отражения от кровли и подошвы которого могут быть различимы, составляет 1/4 длины волны.
В качестве критерия разрешенности Рикер предложил использовать такой временной интервал, на котором суммарный импульс от тонкого слоя будет обладать нулевой кривизной в точке центрального максимума («плоское пятно» (Рисунок 1)). Согласно критерию Рикера предел разрешенности может быть определен путем расчета второй производной импульса.
Рисунок 1: Критерии вертикальной разрешенности (Kallweit and Wood, 1982)
Widess (1973) ввел еще один критерий разрешенности, согласно которому предел разрешенности достигается при мощности слоя равной 1/8 длине волны. Вывод основывается на анализе отражений одинаковых импульсов разной полярности от модели выклинивающегося слоя. (Рисунок 2). По мере сближения двух импульсов находится точка, в которой суммарный импульс становится похож на свою первую производную. При этом разница во временах максимума и минимума не меняется, а меняется только амплитуда суммарного отражения.
Рисунок 2: Модель выклинивающегося слоя (Widess, 1973)
Таким образом, в настоящее время считается, что разрешающая способность равна примерно 1/8 — 1/4 длины волны. В идеальных случаях, например при простом строении среды и в условиях отсутствия помех, при наличии четкого опорного горизонта возможно различать и более близко расположенные границы раздела. (Пейтон, 1982)
Согласно работе (Калинин, Кульницкий, Токарев, 1992), подобное определение вертикальной разрешающей способности представляется неполным и оно появилось в указанном смысле, когда задачей сейсморазведки было в основном изучение кинематики волн, а единственной количественной характеристикой разреза (кроме скорости) являлась мощность слагающих его пластов.
В настоящее время перед сейсморазведкой поставлена задача выделения более сложных объектов (например, сейсмокомплексов, сейсмофаций), характеризующихся набором как кинематических, так и динамических признаков, в той или иной мере выраженных на записи. В связи с этим, при определении разрешающей способности приходится использовать параметры, связанные со временем пробега упругой волны в слое (временная мощность) и перепадом акустических жесткостей на границах слоя (коэффициент отражения). Характеристика разрешающей способности метода через эти величины не может быть рассмотрена без учета способа анализа результатов обработки, среди которых можно выделить два основных вида: а) визуальный анализ сейсмограмм; б) анализ сейсмограмм при помощи компьютера. Такое разделение отвечает реальному процессу извлечения информации из сейсмических данных, так как в одних случаях сейсмические разрезы используются непосредственно для визуального выделения сейсмостратиграфических комплексов и определения их мощности, положения в разрезе и т.д. В других случаях стоит задача выделение отраженных волн от конкретных границ раздела для того, чтобы по их интенсивности и форме (спектру) определить коэффициент отражения, параметры поглощения, рассеяния и др. Таким образом, для каждого способа анализа существует свой оптимальный вид представления результатов, зависящий главным образом от формы результирующего импульса.
Из качественного рассмотрения объектов сейсмических исследований в субгоризонтальных слоистых толщах, искомых параметров и способов анализа результатов следует, что разрешающая способность по вертикали метода отраженных волн определяется тремя основными факторами: 1) надежностью выделения сигнала (характеризует минимальный перепад акустических жесткостей на границах исследуемой толщи при заданном соотношении сигнал/шум); 2)длительностью сигнала (характеризует минимальную временную мощность слоя, при которой интерференция отраженных сигналов не вносит существенных погрешностей в кинематику волнового поля); 3) формой сигнала (отвечает поставленной динамической задаче исследований в рамках используемого способа анализа). (Калинин, Кульницкий, Токарев, 1992).
При таком подходе улучшение разрешенности сейсмической записи сводится к улучшению формы результирующего импульса, т.е. приведение его к виду, максимально отвечающему поставленной задаче при заданных условиях эксперимента и применяемого метода анализа. При этом, для рассмотрения критериев, которым должна удовлетворять форма сигнала или его спектра, рассматривается модель слоя в форме клина с плоскими границами, на который падает импульс, а регистрируется суммарный импульс, отраженный от его кровли и подошвы. В качестве характерных параметров суммарного импульса используются амплитуды центральных экстремумов (Ак, «кажущиеся амплитуды») и расстояние между ними (Тк , «кажущаяся мощность»). (Рисунок 3, 4)
При этом, Тк и Ак могут быть как больше, так и меньше истинных мощностей Т0, А0. При геологической интерпретации таких сейсмограмм отмеченное явление может привести к ложным выводам об ундуляции границ и коэффициентов отражения от них, что в свою очередь может быть необоснованно отнесено к изменению условий осадконакопления и литодинамических характеристик толщи вдоль профиля при фактическом постоянстве характеристик слоя. Происхождение отмеченного эффекта, очевидно, связано с наличием значительных по амплитуде боковых экстремумов относительно главного экстремума.
Рисунок 3: Модель выклинивающегося слоя (Kallweit and Wood, 1982)
| 
Рисунок 4: Кривые кажущейся амплитуды и кажущейся мощности (Okaya, 1995)
|
С точки зрения конечных результатов обработки сейсмограмм авторам статьи (Калинин, Кульницкий, Токарев, 1992) представляется оправданным принять за оптимальную такую обработку, при которой а) отклонение кривой кажущейся мощности пласта Тк от идеальной прямой не превышает заданной величины; б) отклонение кривой кажущейся амплитуды Ак от истинного уровня не превышает заданной величины.
Условия (а) и (б) могут иметь место в варианте «и-и», либо «или-или». В последнем случае, по необходимости, обработку возможно проводить по различным алгоритмам.
Первый критерий задает минимальную мощность просто, оценка его временной мощности по положению центральных экстремумов не превышает допустимой погрешности. Эту величину можно назвать разрешающей способностью по линейному критерию. Можно показать, что смещение центрального экстремума относительно его истинного положения вследствие интерференции с соседним импульсом определяется его первой производной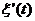 
. Поэтому, оптимальной для кинематического критерия разрешенности будет функция 
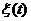, с максимально быстро падающей первой производной.
Оптимальное поведение функции 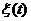для задачи увеличения динамической разрешающей способности Ак, очевидно, требует максимально быстрого спада самой функции 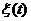до заданного уровня при удалении ее от абсолютного экстремума. (Калинин, Кульницкий, Токарев, 1992)