Beylkin (1985) вывел уравнение, позволяющее рассчитать («восстановить») контраст акустических импедансов как функцию координаты x(x, y, z) сейсмических измерений с ограниченной апертурой. Ограниченная апертура определяется значениями 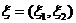 , где
, где 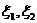 - пространственные координаты. Показано, что наблюденные данные преобразуются в обработанные с использованием отображения
- пространственные координаты. Показано, что наблюденные данные преобразуются в обработанные с использованием отображения 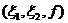 (координаты наблюденных данных, где
(координаты наблюденных данных, где 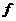 - частота) в (
- частота) в (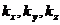 ) (координаты обработанных данных). Отображение можно записать так:
) (координаты обработанных данных). Отображение можно записать так: 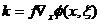 , где
, где 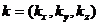 - вектор волнового числа в преобразованной (мигрированной) области,
- вектор волнового числа в преобразованной (мигрированной) области, 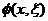 - плоскость времен пробега (так же называемая миграционным оператором) для дифрагирующего объекта в точке x для пар источник/приемник, описываемых
- плоскость времен пробега (так же называемая миграционным оператором) для дифрагирующего объекта в точке x для пар источник/приемник, описываемых 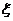 .
. 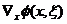 является производной
является производной 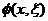 по отношению к точке восстановления x;
по отношению к точке восстановления x; 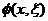 должна вычисляться исходя из скоростной модели среды.
должна вычисляться исходя из скоростной модели среды.
Данное уравнение преобразует 5Д плоскость времен пробега 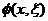 в 3Д волновые числа. Преобразование согласуется с тем фактом, что в случае миграции до суммирования, каждая трасса, описываемая
в 3Д волновые числа. Преобразование согласуется с тем фактом, что в случае миграции до суммирования, каждая трасса, описываемая 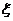 , служит для восстановления набора результативных точек (x, y, z). Таким образом, уравнение определяет область наблюдений Dx в пространстве волновых полей (диапазон пространственных частот 3Д). Beylkin утверждает, что описание Dx по сути является определением горизонтальной разрешающей способности. Чем больше область покрытия k, тем выше возможная разрешающая способность.
, служит для восстановления набора результативных точек (x, y, z). Таким образом, уравнение определяет область наблюдений Dx в пространстве волновых полей (диапазон пространственных частот 3Д). Beylkin утверждает, что описание Dx по сути является определением горизонтальной разрешающей способности. Чем больше область покрытия k, тем выше возможная разрешающая способность.
Пространственная разрешающая способность для заданной точки x, определенной посредством Dx, зависит от: (1) объема интегрирования в целом, который определяется положением источников и приемников, (2) полосы частот используемого сигнала.
Нет необходимости анализировать весь объем данных в k. Максимальное волновое число (относящееся к максимальному градиенту 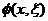 ) может служить приемлемым критерием разрешающей способности, при условии, что k=0 входит в диапазон волновых чисел.
) может служить приемлемым критерием разрешающей способности, при условии, что k=0 входит в диапазон волновых чисел.
Дифрагированная волна 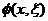 может быть описана следующим образом:
может быть описана следующим образом:
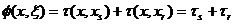 , где
, где 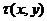 - время прохождения волны от точки поверхности y до точки среды x. В общем виде k может быть записано в виде векторной суммы
- время прохождения волны от точки поверхности y до точки среды x. В общем виде k может быть записано в виде векторной суммы 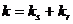 , где ks и kr – вклады источника и приемника в вектор волнового числа k. Можно показать, что производная по направлению времен прохождения
, где ks и kr – вклады источника и приемника в вектор волнового числа k. Можно показать, что производная по направлению времен прохождения  и
и 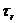 по отношению к x является направлением соответствующих траекторий лучей. Таким образом, ks и kr ориентированы в направлении лучей в точке x. (Рисунок 12) Каждая пара источник/приемник в расстановке согласовываются с k в области волновых чисел.
по отношению к x является направлением соответствующих траекторий лучей. Таким образом, ks и kr ориентированы в направлении лучей в точке x. (Рисунок 12) Каждая пара источник/приемник в расстановке согласовываются с k в области волновых чисел.
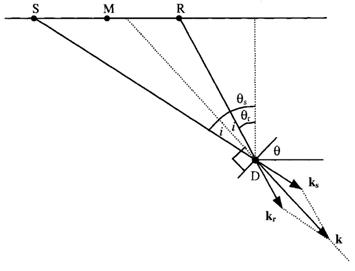
Рисунок 12: Освещение дифрактора D парой источник/приемник (S/R). Направления лучей в точке D определяют компоненты волновых чисел источника и приемника общего волнового числа k. SD и RD – траектории лучей для отражающей границы в точке D с углом наклона 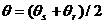 . Траектории лучей составляют угол
. Траектории лучей составляют угол 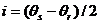 с вектором волнового числа (Vermeer, 1999)
с вектором волнового числа (Vermeer, 1999)
Как видно из уравнения 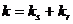 и (Рисунок 12), самыми лучшими являются данные с нулевым выносом, в связи с тем, что ks и kr совпадают.
и (Рисунок 12), самыми лучшими являются данные с нулевым выносом, в связи с тем, что ks и kr совпадают.
Исходя из вышесказанного, можно рассмотреть Dx для среды с постоянной скоростью 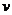 , в случае совмещенного источника и приемника. Для точки
, в случае совмещенного источника и приемника. Для точки 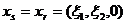 уравнение запишется следующим образом:
уравнение запишется следующим образом: 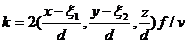 , где d – расстояние от источника (и приемника) до точки среды х. Вектор в круглых скобках – единичный вектор от xs к x.
, где d – расстояние от источника (и приемника) до точки среды х. Вектор в круглых скобках – единичный вектор от xs к x.
Рассмотрим случай двумерного профиля с совмещенным источником и приемником. Направление профиля совпадает с направлением оси x. Максимальные значения kx и kz могут быть записаны так:
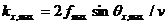 ,
, 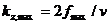 , где
, где 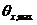 - угол между вертикалью и траекторией луча из вычисляемой точки до самой дальней пары источник/приемник.
- угол между вертикалью и траекторией луча из вычисляемой точки до самой дальней пары источник/приемник.
Существует разница между горизонтальной и вертикальной разрешающей способностью: kx достигает максимума при максимальном значении d в направлении оси x, в то время как kz достигает максимума при минимальном значении d (таким образом, 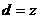 , следовательно,
, следовательно, 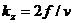 ). Следствием этого является возможность улучшения пространственной разрешающей способности путем использования большей апертуры миграции, таким образом учитывая крутопадающие части дифрагированных волн, в то время как вертикальная разрешающая способность не зависит от апертуры.
). Следствием этого является возможность улучшения пространственной разрешающей способности путем использования большей апертуры миграции, таким образом учитывая крутопадающие части дифрагированных волн, в то время как вертикальная разрешающая способность не зависит от апертуры.
На основе работы (Kallweit and Wood, 1982) Vermeer предлагает производить расчеты по аналогии, но для пространственных частот, для направления 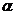 (
(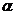 = x или y) (
= x или y) (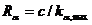 ):
):
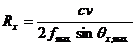 ,
,  , где с – коэффициент пропорциональности.
, где с – коэффициент пропорциональности.
В случае 2Д наблюдений вдоль профиля по методике ОГТ минимальную горизонтальную разрешенность можно выразить в следующем виде:
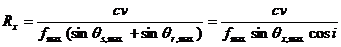 , где
, где 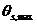 и
и  - углы между вертикальной осью и траекториями лучей пары источник/приемник с максимальным расстоянием их центра M от исследуемой точки,
- углы между вертикальной осью и траекториями лучей пары источник/приемник с максимальным расстоянием их центра M от исследуемой точки, 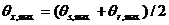 (то есть, максимальный угол, освещаемый парой источник/приемник) и
(то есть, максимальный угол, освещаемый парой источник/приемник) и 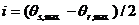 (угол падения лучей для максимального угла падения отражающего горизонта).
(угол падения лучей для максимального угла падения отражающего горизонта).