Разрешающая способность по горизонтали определяет минимальное расстояние между двумя объектами, относящимся к одной поверхности, на котором эти объекты могут быть различены по отдельности. Пространственную разрешающую способность можно определить иначе как минимальный размер неоднородности рельефа, при котором эту особенность можно выявить по данным сейсморазведки. (Старовойтов, Шалаева, 2010). Традиционно, критерием разрешающей способности по горизонтали в сейсморазведке считается размер первой зоны Френеля.
Понятие зон Френеля пришло в сейсморазведку из оптики (Рисунок 5): L – монохроматический источник света с длиной волны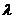 
, О – точка наблюдения, АВ – отверстие в экране, АС – радиус первой зоны Френеля, если LAO = LCO + 
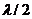. В случае сейсморазведки (Рисунок 6), АС – радиус первой зоны Френеля, если LA = LC + 
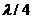. (Bruhl, Vermeer, Kiehn, 1996).
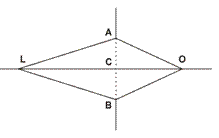Рисунок 5: Определение первой зоны Френеля в оптике
| 
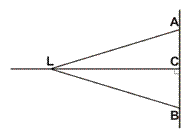Рисунок 6: Определение первой зоны Френеля в сейсморазведке
|
Для того, чтобы определить понятие горизонтальной разрешающей способности, необходимо выяснить, какая область отражающей границы вносит основной вклад в формирование отраженной волны. Рассуждения о том, что отражение происходит от некоторой точки, верны были бы только в том случае, если бы сейсмический импульс имел бесконечно малую длительность, а длина преобладающей волны была бы бесконечно малой. В реальности мы имеем дело с сигналами конечной длительности и ограниченного частотного состава, поэтому область отражения может иметь значительные размеры. Существуют различные подходы к определению размера этой области. Идея этих подходов заключается в рассмотрении разности времен прихода волн, отраженных от центра и от края круглой площадки. (Шалаева, Старовойтов, 2010). Как известно, волны интерферируют не ослабевая друг друга, пока различие в их временах пробега не превышает четверти периода. Поэтому, в качестве меры горизонтальной разрешающей способности принята площадка, в пределах которой интерференция будет конструктивной, т.е. интенсивность суммарной волны не будет меньше, чем интенсивность волн по отдельности.
|
|
Некоторые авторы (например, Berkhaut) предлагают использовать при определении размера зон Френеля различие во временах пробега, равное одной восьмой периода волны. Помимо этого, Berkhaut определяет первую зону Френеля как площадь, полностью возвращающую заданное количество энергии. (Bruhl, Vermeer, Kiehn, 1996)
Рассмотрим сферический фронт, который отражается от горизонтальной отражающей поверхности АА’. Эта отражающая граница может быть представлена непрерывной совокупностью точечных дифрагирующих объектов. При совмещенном на поверхности земли источнике и приемнике (в точке S), энергия от точки О дойдет за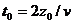 
. Теперь пусть падающий волновой фронт переместится на величину 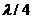. Энергия от точки А или А’ достигнет приемника за время 
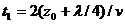. Энергия, отраженная от всех точек, расположенных внутри отражающей поверхности с радиусом ОА’, придет между 
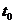и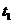 
. Вся энергия, пришедшая за временной интервал 
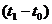, что соответствует половине видимого периода 
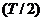, будет конструктивно интерферировать. (Рисунок 7)
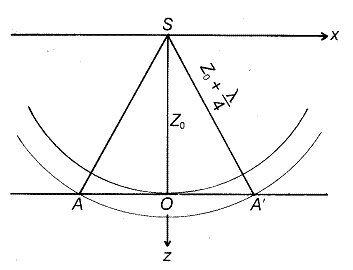
Рисунок 7: Зона Френеля (АА') (Уилмаз, 2001)
Отражающая площадка АА’ называется полуволновой зоной Френеля (Hilterman, 1982) или первой зоной Френеля (Sheriff, 1984). Две отражающие точки, попавшие в эту зону, не могут быть различены, при проведении съемки с поверхности. (Yilmaz, 2001)
|
|
Учитывая, что ширина зоны Френеля зависит от длины волны, она так же зависит и от частоты. Таким образом, для относительно высокочастотного сигнала, зона Френеля будет достаточно узкой. Чем уже зона Френеля, тем проще различить два объекта, находящихся на расстоянии друг от друга. Таким образом, ширина зоны Френеля является мерой горизонтальной разрешающей способности. Кроме частоты горизонтальная разрешающая способность так же зависит от скорости и глубины отражающей границы (от радиуса волнового фронта):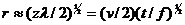 
.
Развивая концепцию зоны Френеля, можно выделить не только первую зону, но и зоны второго, третьего и более высоких порядков, однако их вклад в генерацию и формирование отражения незначителен по сравнению с первой зоной, поэтому обычно принимают во внимание только первую зону Френеля. (Пейтон, 1982). По некоторым оценкам, вклад первой зоны Френеля в энергию отраженной волны составляет около 86%.
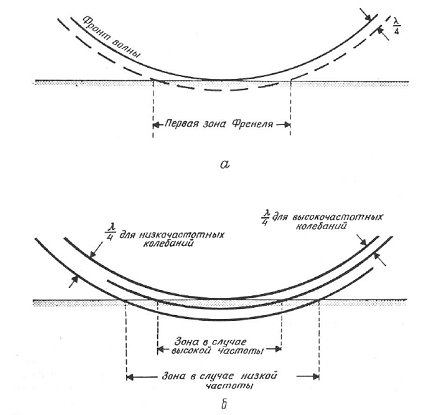
Рисунок 8: Первая зона Френеля. а – случай отражения сферической волны от плоской границы раздела. б – влияние частоты колебаний на размер зоны Френеля (Пейтон, 1982)
В проведенном выше рассмотрении подразумевался точечный источник, для которого траектория распространения волн от источника к приемнику отличаются для последовательных зон Френеля на полупериод. Зоны Френеля иногда выделяют по отношению к плоской падающей волне, а не к сферической. В этом случае различия в полупериод между последовательными зонами Френеля должны быть целиком отнесены к части траектории от отражающей границы к приемнику. Такое допущение приводит к расширению зоны Френеля, и радиус зоны определяется как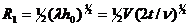 
(Шериф, 1987).
|
|
Поскольку длина волны зависит от частоты, размеры зоны Френеля также зависят от частоты (Рисунок 8, б). Следовательно, разным частотным компонентам сейсмической волны будут соответствовать разные по величине эффективной площади участки отражающей поверхности (Пейтон, 1982). Поэтому, говоря о размере первой зоны Френеля и используя это понятие как меру горизонтальной разрешающей способности сейсмоакустических исследований, нужно помнить, что в классическом рассмотрении, речь идет о размере первой зоны Френеля для монохраматического сигнала.