Как уже говорилось выше, традиционно понятие зон Френеля вводится для монохроматического сигнала. Но при проведении сейсмоакустических работ используются источники, создающие широкополосные сигналы. Поэтому, говоря о зонах Френеля, необходимо рассмотреть эффекты, возникающие при использовании таких сигналов.
В работе (Knapp, 1991) рассматриваются результаты моделирования отражений от круглых отражающих поверхностей увеличивающегося диаметра. Данные были получены для совмещенного источника и приемника. Расчеты производились в частотной области по формуле Trorey (1970):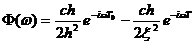 
, где Φ – потенциальная функция, с – константа, связанная с коэффициентом отражения, T0 – двойное время пробега волны, h – глубина до отражающей площадки (
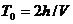), T – двойное время пробега до края отражающей площадки и ξ – расстояние до края площадки (
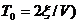. (Рисунок 9) В общем случае, с включает в себя функцию источника, однако автор статьи ею пренебрегают.
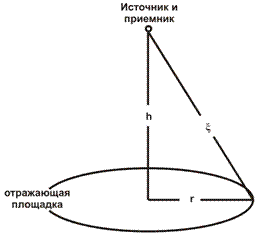
Рисунок 9: Модель круглой отражающей площадки
Первый член уравнения характеризует однократно отраженную волну, а второй соответствует дифракции, то есть краевым эффектам. Однократное отражение независимо от радиуса ξ, и только амплитуда зависит от глубины h и коэффициента отражения c. Дифракция также независима от частоты.
Уравнение легко выражается для временной области, используя свойства временного сдвига: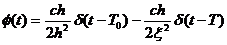 
. В этом уравнении первый член также соответствует первому отражению с амплитудой 
на времени T0. Второй член соответствует дифракции, имеющей обратную полярность, с амплитудой 
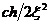на времени T. Амплитуда отражения зависит только от коэффициента отражения и глубины, а время отражения – константа. Амплитуда дифракции зависит от размера отражающей площадки (
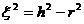). Время дифракции также зависит от размера отражающей площадки (
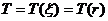). Таким образом, 
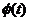зависит от размера отражающей площадки, хотя однократное отражение не зависит от размера площадки.
Считать свойства доминирующей частоты или кажущейся частоты широкополосного сигнала такими же, как и монохромного сигнала, не корректно. Между ними есть большая разница, особенно во временной области. Математически, монохроматический сигнал бесконечен во времени и является идеальной синусоидой. Сейсмический импульс ограничен во времени и его длительность определяется кажущейся частотой. Кажущаяся частота зачастую соответствует доминирующей частоте – пик на амплитудном спектре – но это не всегда так. Для широкополосного сигнала с равномерным спектром, кажущаяся частота представлена двумя третями от максимального значения частоты. (Knapp, 1991)
Trorey (1970) показал, что суммарный отклик от отражающей площадки можно разложить на две компоненты: отражение от площадки и краевые эффекты (дифракции). Понятие зон Френеля и дифракций имеют общую природу. Так, например, на сейсмических данных дифракции от разломов имеют большую латеральную протяженность, нежели сами разломы. Следовательно, предположения, основанные на зонах Френеля, корректны. Проблема состоит в том, что в случае широкополосных сигналов дифракции (1) уменьшаются в процессе обработке по методике ОГТ и (2) они разделены с отражениями по времени, вследствие чего дифракции могут быть утеряны при наложении следующих отражений.
Для монохромных сигналов отражение от площадки и дифракция взаимосвязаны и их интерференция зависит от амплитуды и фазы отраженного сигнала. В первой зоне Френеля дифракция конструктивно интерферирует с отражением. Во второй зоне начинается деструктивная интерференция, заключающаяся в уменьшении энергии отраженного сигнала. (Рисунок 10, а) С увеличением размера отражающей площадки, дифракция уменьшается в амплитуде и контраст между соседними зонами приходит в соответствие с базисным откликом всей системы. (Knapp, 1991)
Для широкополосных сигналов отражение от площадки и дифракция разделены во времени. Они становятся независимыми, когда размер отражающей площадки достаточно велик. В процессе обработки данных ОГТ, дифракции подавляются, в связи с тем, что суммируются не с той скоростью, особенно на дальних расстояниях от дифрагирующего объекта. По мнению Knapp’а это приводит к нарушению принципа зон Френеля.
В статье (Bruhl, Vermeer, Kiehn, 1996) предлагается представить решение уравнения (Trorey) в другом виде: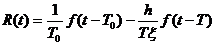 
, где R(t) – отраженный сигнал, 
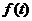- импульс источника. Первый член соответствует отражению на времени Т0 с учетом геометрического расхождения 1/Т0. Второй член – импульс источника обратной полярности с временной задержкой Т (связанный с краевым эффектом, вызываемым конечной областью интегрирования). В случае отражающей площадки с бесконечным радиусом R(t) точно соответствует искомому отражению.
На (Рисунок 10, а) представлен монохроматический сигнал и радиусы зон Френеля. Первый максимум кривой определяет границы первой зоны Френеля, другие экстремумы определяют радиусы других зон. Функция энергии сигнала соответствует похожей функции, описанной у (Knapp, 1991).
Рисунок 10: Зоны Френеля для различных импульсов. Центральная частота 37.1 Гц, глубина 1000 м, скорость 2000 м/с. (а) Монохроматический сигнал (б) Узкополосный сигнал (в) Широкополосный сигнал (Bruhl, Vermeer, Kiehn, 1996)
Для сигналов с относительно узким спектром (Рисунок 10, б) функция энергии осциллирует в той же мере. Осцилляции, тем не менее, исчезают на расстоянии, соответствующем 
, за рамками которого отражение и краевые эффекты разделены. Энергетическая функция широкополосного сигнала вначале растет похоже на остальные сигналы, но быстро выравнивается. (Рисунок 10, в) Затем энергия монотонно уменьшается, что связано с уменьшением влияния второго члена уравнения. Сравнение различных энергетических функций дало возможность обобщить определение первой зоны Френеля для широкополосных сигналов: Граница первой зоны Френеля находится в соответствии с позицией максимума энергии.
Таким же образом можно обобщить определение зон Френеля, которое представил Berkhaut: Первая зона Френеля для широкополосного сигнала соответствует наименьшей зоне, энергия отраженных волн от которой равна энергии источника.
Таким образом, согласно исследованиям (Bruhl, Vermeer, Kiehn, 1996), радиус первой зоны Френеля определяется как преобладающей частотой в спектре, так и шириной полосы.