Б) ЭКСЕРГИЯ ТЕПЛОВОГО ПОТОКА

Эксергия e_q теплового потока q определяется уравнением

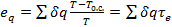. (3-13)

В частном случае при T =const и 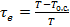формула (3-13) принимает вид:

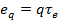. (3-14)

Входящая в эти выражения величина 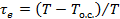, равная термическому КПД цикла Карно между температурами Т и , так же как и е,является функцией состояния системы и окружающей среды, зависит при фиксированном значении только от T и включает наряду с параметром состояния Т и значение параметра окружающей среды .

Необходимо подчеркнуть, что, как показал И. А. Вышнеградский [40, 41], классический обратимый цикл Карно − не единственный цикл, термический к. п. д. которого равен 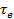(подробнее об этом в гл. 4).

Функция 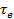пригодна для оценки любых взаимных преобразований тепла и работы, проводимых как посредством циклов с потоками рабочего тела, так и без них (например, в полупроводниковых или термомагнитных охладителях). В любом случае величина 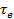показывает предельные возможности такого преобразования независимо от вида устройства, в котором оно производится.

В отличие от 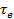второй сомножитель выражения (3-13) −величина 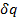− не дифференциал параметра состояния. Поэтому эксергия тепла e_q вотличие от е не параметр состояния, а зависит от пути процесса. Вместе с тем связь между величинами e_q и q аналогична в одном важном отношении связи между е и h:как и h величина q не содержит сама по себе никаких качественных характеристик теплового потока, мерой же его пригодности к превращению в работу служит для теплового потока величина e_q, так же, как для потока вещества − е.

Поскольку величина e_q зависит от эксергетической температурной функции 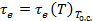, рассмотрим свойства этой функции более подробно.

Связь между 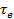и Т определяется уравнением

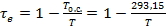(3-15).

В прямоугольной системе координат зависимость 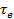от T будет изображаться гиперболой, пересекающей ось абсцисс 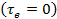в точке Т= 293,15 К. При 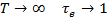, а при 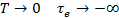. Таким образом, величина 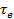может принимать вес действительные значения в интервале от 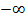до +1. Область положительных значений 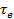соответствует абсолютным температурам от до 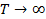, а область отрицательных значений 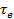− температурам ниже , вплоть до абсолютного нуля.

Изменение знака 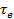при переходе через приводит к соответствующему изменению знака эксергии теплового потока. При температурах выше знаки e_q и q одинаковы. При температуре ниже знаки потоков тепла и эксергии противоположны.

По мере приближения к 0 К при конечном значении q абсолютная величина e_q вместе с 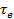стремится к бесконечности.

На рис. 3-3 качественно показана в T, s-координатах связь между величиной теплового потока и его эксергией. Количество отводимого при низких температурах T ₀ тепла q ₀,которое на рисунке обозначено незаштрихованными площадями, одинаково для всех трех случаев. Разница между показанными процессами состоит в том, что температуры Т ₀различны .

Из графика видно, как быстро возрастает работа, равная эксергии тепла e_q (на рисунке обозначена заштрихованной площадью − 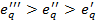), которую нужно затратить для отвода па каждом уровне T ₀ соответствующего теплового потока q ₀. Суммарная площадь обеих площадок показывает количество тепла q, отводимое в каждом случае в ок­ружающую среду при .

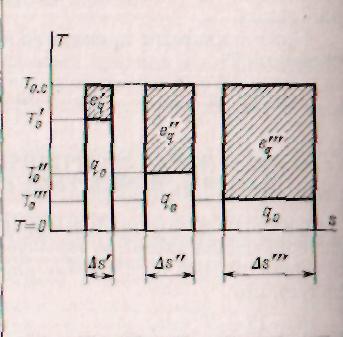
Рис. 3-3. Связь величин отводимого при низкой температуре Т ₀ <. тепла q и величины e_q равной минимальной работе.

Эту же зависимость можно видеть из построений на рис. 3-1. Чем ниже расположена горизонтальная прямая fg (т. е. чем ниже температура), тем больше (при том же значении q ₂)отрезок kh, изображающий .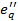

При 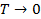К точка h уходит в бесконечность.

В пределе при К величины 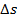и 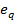в соответствии с рис. 3-3 должны были бы стремиться к бесконечности. Однако такое графическое построение недопустимо при 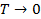К, поскольку, как уже указывалось выше, по закону Нернста при этих условиях s =0.

По этой же причине при 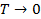К формула (3-14), так же как и формула (3-6), неприменима [3, 4].

Изменение температуры окружающей среды меняет значение 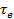и, следовательно, e_q при неизменных q и Т. Однако относительное увеличение затраты работы невелико из-за быстрого роста абсолютной величины 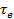с понижением температуры Т.

Анализ уравнения

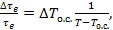(3-16)

полученного из формулы (3-15), показывает, что относительная ошибка определения 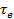при изменении тем меньше, чем больше температура T отличается от .

При 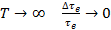, а при . В области, близкой к относительная ошибка быстро возрастает, стремясь к бесконечности при T = . Поэтому влияние изменения существенно сказывается на показателях холодильных установок и незначительно − криогенных.

Ниже в качестве примера даны значени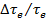я для 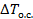=10 К при различных Т:

в) СВЯЗЬ МЕЖДУ ЭКСЕРГЕТИЧЕСКОЙ ТЕМПЕРАТУРНОЙ ФУНКЦИЕЙ И ЭКСЕРГИЕЙ е ПОТОКА ВЕЩЕСТВА

Связь между функциями 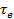и е обусловлена тем, что величина, характеризующая эксергию термического взаимодействия, должна входить составной частью в уравнение для е. Действительно, из уравнения (3-6) следует, что

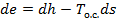(3-17)

при p=const

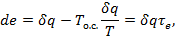
откуда

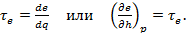(3-18)

Частная производная термомеханической эксергии потока по энтальпии при постоянном давлении равна эксергетической температурной функции .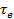

Из уравнения (3-18) также следует, что 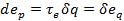. Для конечного процесса

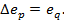(3-19)

Изменение эксергии е потока вещества в изобарном процессе равно эксергии e_q связанного с этим процессом теплового потока q.

Зависимость (3-19) имеет большое практическое значение, так как большинство процессов теплообмена протекает в изобарных или близких к ним условиях. Во всех этих случаях подсчет эксергии тепла через 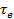можно не проводить, а получить величину 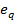по разности 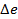. Это особенно удобно при переменной температуре, когда точный подсчет 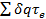может оказаться трудоемким и сложным.