ЗАДАЧИ ТЕРМОДИНАМИЧЕСКОГО АНАЛИЗА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

ОСНОВЫМЕТОДИКИ ТЕРМОДИНАМИЧЕСКОГО АНАЛИЗА НИЗКОТЕМПЕРАТУРНЫХ ТЕХНИЧЕСКИХ СИСТЕМ

ЗАДАЧИ ТЕРМОДИНАМИЧЕСКОГО АНАЛИЗА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Термодинамический анализ представляет собой метод термодинамического исследования технических систем (как в целом, так и посредством их декомпозиции) с целью получения наиболее полной информации о процессах преобразования энергии, происходящих в них [3,5,23,38,39].

Формы энергии, участвующие во всех энергетических превращениях, могут быть сведены к двум видам: к первому, куда относятся формы энергии, полностью превратимые в любые другие формы; ко второму, куда относятся те формы, которые не могут быть в общем случае полностью преобразованы в другие формы энергии.

Энергия первого вида (например, электрическая, механическая, магнитная и др.) в силу своей превратимости, не зависящей от параметров окружающей среды, может быть в пределе полностью использована в технических целях. Все формы энергии такого вида равнозначны не только количественно, но и качественно. Для анализа таких технических систем и их элементов, внутри которых не накапливается и не расходуется энергия, без ограничений применимо уравнение

, (3-1)

Где и − суммы соответственно подведенных и отведенных потоков энергии.

На основе баланса (3-1) составляются уравнения для вычисления безразмерных коэффициентов, характеризующих различные системы преобразования энергии. Все они построены по формуле

(3-2)

где величины SW ₁и SW ₂ показывают суммы потоков энергии, выбираемых для каждой системы ad hoc, причем величина SW ₁ должна показывать полезный технический эффект процесса, a SW ₂ − затраты энергии на его проведение.

Все балансовые расчеты, относящиеся к энергии первого вида, могут вестись на основе только первого начала термодинамики.

Формы энергии второго вида (например, внутренняя энергия рабочего тела, энергия, передаваемая в виде теплового потока и др.) качественно различны, поскольку степень их «неорганизованности», характеризуемая энтропией, различна. Границы превратимости таких форм энергии связаны не только с параметрами, ее определяющими, но и с параметрами окружающей среды. В пределе при равенстве параметров рабочего тела и окружающей среды техническая ценность его энергии равна нулю.

При решении инженерных задач в области низкотемпературной техники необходимо учитывать, что в них участвуют формы энергии как первого, так и второго вида.

Мерой превратимости, пригодности заданного количества энергии любого вида, характеризуемой энтропией, служит количество энергии, не связанной с энтропией (равное, например, механической или электрической работе), которое может быть получено из нее в обратимом процессе взаимодействия с окружающей средой. Условия такого преоб­разования определяются вторым началом термодинамики. Эта мера пригодности любого вида энергии и была названа эксергией [5, 38].

Следовательно, эксергия термодинамической системы в данном состоянии определяется количеством энергии, не характеризуемой энтропией, которое может быть получено внешним приемником энергии от системы при ее обратимом переходе из данного состояния в состояние полнаго равновесия с окружающей средой.

Рассматриваемая система может быть как термодинамической (например, некоторое количество рабочего тела в замкнутом объеме или в потоке), так и технической (например, установка класса L, R или D).

Окружающая среда ¹характеризуется тем, что ее параметры не зависят от параметров рассматриваемой системы и тем, что все ее компоненты должны находиться в полном термодинамическом равновесии. (В действительности же, в окружающей среде существуют градиенты температур, давлений и химических потенциалов. Однако при решении подавляющего большинства задач этими обстоятельствами можно пренебречь. Поэтому использование понятия окружающей среды, как и других термодинамических абстракций, весьма плодотворно и практически необходимо.)

¹ Здесь и в дальнейшем под термином «окружающая среда» понимается равно-иан часть внешней среды, находящейся вне границ системы.

Параметры окружающей среды в большинстве задач могут считаться постоянными. Однако в ряде случаев эти параметры могут изменяться (например, в авиационных системах при разных высотах, под влиянием климатических условий и др.).

В подавляющем большинстве задач для полной характеристики окружающей среды достаточно знать температуру T _o.с, давление р _o.с и химический состав. До тех пор, пока все параметры системы и ее частей не сравняются с соответствующими параметрами окружающей среды, равновесие не будет достигнуто и система во взаимодействии со средой может произвести и отдать некоторую внешнюю работу, что означает, что она обладает определенной эксергией. В ряде случаев система, не отдавая энергию (и даже получая ее), может производить работу за счет окружающей среды (примером такой системы является сосуд, в котором давление меньше атмосферного). При полном равновесии системы и среды эксергия равна нулю. Такое состояние системы называется нулевым (в литературе на английском языке dead state − «мертвое состояние»).

Внешние объекты − источники и приемники энергии − характеризуются прежде всего тем, что в них хотя бы один из определяющих параметров отличается от параметров окружающей среды. Вследствие этого они могут быть использованы в качестве внешних источников эксергии для «питания» системы и обеспечения ее непрерывного функцио­нирования (например, топливо, излучение с температурой, отличной от разновесной, сжатый природный газ, термальные воды и т. д.).

Из первого и второго начал термодинамики непосредственно следует, что в каждом данном состоянии эксергия системы, так же как и энергия, имеет определенное фиксированное значение.

Взаимодействие системы с окружающей средой может проходить как обратимо (идеальный процесс), так и необратимо (реальный процесс).

В идеальном процессе будет получена работа, равная эксергии. Если процесс будет остановлен до наступления равновесия системы и среды, то полученная работа будет равна убыли эксергии системы.

В реальном процессе работа будет меньше, чем убыль эксергии (в пределе работа может быть равна нулю). Это означает, что часть эксергии не превратится в работу, а исчезнет, будет потеряна. В этом состоит одно из существенных отличий эксергии от энергии. Эксергии подчиняется закону сохранения только в обратимых процессах; во всех остальных случаях (реальные системы) она может частично или полностью исчезать, теряться в результате диссипации (рассеяния) энергии в необратимых процессах. Естественно, что чем меньше эта потеря эксергии, тем процесс термодинамически совершеннее.

Составляя уравнения типа (3-1) и (3-2) применительно к эксергии Е,мы делаем их универсальными и полностью пригодными для любых термодинамических систем, независимо от видов энергии, участвующих в процессе:

(3-3)

или

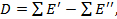(3-3а)

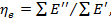(3-4)

где и − суммы соответственно подведенных и отведенных потоков эксергии; D − потеря эксергии (* от dissipation − диссипация, рассеяние; диссипация энергии характеризуется ис-иовеиием, уничтожением, потерей соответствующего количества эксергии).

В отличие от уравнений (3-1) и (3-2), отражающих энергетический баланс, уравнения (3-3), (3-3а) и (3-4) отражают эксергетический баланс системы, т. е. опираются как на первое, так и на второе начала термодинамики.

Эксергетический баланс в отличие от энергетического баланса во всех случаях показывает величину потерь от необратимости в системе и степень ее термодинамического совершенства.

Величины 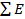включают эксергию тех видов веществ и энергии, которые входят в энергетический баланс рассматриваемой технической системы. Применительно к низкотемпературной технике 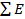включает эксергию потока вещества Е _мэксергию теплового потока E_q, а также работу L (равную Е для механической или электрической энергии).

Из уравнения (3-3) следует, что эксергия любого вида в обратимых процессах может быть переведена полностью в эксергию любого другого вида независимо от направления этих процессов.

Для низкотемпературных систем в общем случае необходимо при расчете величин эксергии учитывать взаимодействия трех возможных видов в самой системе и между системой и окружающей средой: термические (обобщенная сила − температура T), деформационные (обобщенная сила − давление р) и химические (обобщенная сила − химический потенциал m). Последний вид взаимодействий связан большей частью с обменом веществом между системой и окружающей средой, поэтому он характерен для открытых систем, например установок класса D.

Эксергия потока вещества E_м состоит из двух составляющих: термомеханической (или физической) и нулевой (или химической). Первая связана с различием термических (D T) и механических (D р)параметров вещества и среды и измеряется количеством работы, которое может быть получено в обратимом процессе установления равновесия потока вещества со средой посредством энергетического взаимодействия, но без обмена материей (при этом р→р _o.c и Т→Т _o.c.).

Вторая составляющая связана с установлением равенства химических потенциалов между соответствующими компонентами рабочего тела и окружающей среды . Она измеряется количеством работы, которое может быть получено в обратимом процессе установления равновесия компонентов рабочего тела данного состава с соответствующими компонентами окружающей среды при р _о.с. и Т _o.c.. Вещество находится в так называемом нулевом состоянии, так как термомеханические параметры рабочего тела находятся в равновесии с параметрами среды. Термин «нулевая», кроме того, удобнее, поскольку отражает тот факт, что процессы взаимодействия с окружающей средой, связанные с обменом массой, не всегда сопровождаются химическими реакциями (например, разделение смеси газов или процессы смешения и растворения).

Эксергия теплового потока E_q при температуре Т определяется количеством работы, которое может быть получено (или должно быть затрачено) в обратимом процессе переноса энтропии, характеризующей данный тепловой поток, на уровень температуры Т _o.c..

Рис. 3-1. Взаимные преобразования тепла и работы на Т, q -диаграмме.

Горизонтальная линия Т _o.c.обозначает температуру окружающей среды.

Встречающаяся иногда формулировка этого положения посредством термина «перенос тепла» не точна потому, что количество тепла, отдаваемого системой, не равно количеству получаемого тепла, а отличается от него на величину работы. Поток энтропии, напротив, в обратимом процессе взаимного превращения тепла и работы сохраняет свое значение. Это положение наглядно иллюстрируется диаграммой температура Т − количество тепла q, показанной на рис. 3-1. Подробные комментарии к диаграмме даны в [5]. Из рисунка нетрудно видеть, что энтропии, характеризующие тепловой поток q ₁, поступающий в систему, и поток 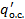, отдаваемый системой в окружающую среду, равны между собой:

(3-5)

т. е. величина потока энтропии, проходящей через систему, при переносе с уровня Т ₁на не изменяется.

Точно так же тепловой поток q ₂ при T ₂< характеризуется энтропией 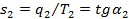. При переносе этой энтропии на уровень она также не изменится. Работа (эксергия 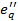), которую необходимо затратить на этот перенос энтропии, − l ₂ будет равна отрезку kh.

Понятие эксергии теплового потока применимо также ко всем случаям переноса энергии путем теплопроводности или конвекции.