Термомеханическая (физическая) эксергия
Рассмотрим установившийся поток рабочего тела, имеющего параметры и, v, s, T и р. Значения параметров, характеризующие состояние равновесия со средой, обозначим через  ,
,  ,
,  ,
,  и
и  . Для определения эксергии е потока требуется найти максимальную его работу при переходе от данного состояния к нулевому [5, 38] по выражению
. Для определения эксергии е потока требуется найти максимальную его работу при переходе от данного состояния к нулевому [5, 38] по выражению
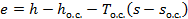 (3-6)
(3-6)
Функция е − эксергетическая функция, поскольку однозначно определяемое параметрами вещества и среды ее значение связано непосредственно только с температурой  .
.
Свойства эксергетической функции е необходимо рассмотреть относительно подробно, поскольку поточные процессы занимают в технике низких температур доминирующее положение.
Уравнение (3-6) определяет значение е в зависимости от калорических параметров состояния h и s. Для исследования функции е полезно также определить ее зависимость от давления рабочего тела и его температуры.
Физическая трактовка зависимости е=е (р, Т)может быть дана посредством устройства, показанного на рис. 3-2. Устройство состоит из обратимой изотермической расширительной машины (или компрессора) 1, работающей при Т=  ,системы с обратимым циклом 2для преобразования теплового потока q в работу и тела 3(отличного от системы и среды), которое может получать или отдавать работу1. Устройство находится в среде с параметрами
,системы с обратимым циклом 2для преобразования теплового потока q в работу и тела 3(отличного от системы и среды), которое может получать или отдавать работу1. Устройство находится в среде с параметрами  ,
,  ;к нему подводится стационарный поток рабочего тела с параметрами р и T. В работе [5] анализируются два случая определения характера изменения эксергии потока вещества по максимальной работе:
;к нему подводится стационарный поток рабочего тела с параметрами р и T. В работе [5] анализируются два случая определения характера изменения эксергии потока вещества по максимальной работе:
Первый случай (рис. 3-2, а); р >  . Общее количество работы, получаемой телом 3, равное эксергии е, составляет
. Общее количество работы, получаемой телом 3, равное эксергии е, составляет  .
.
Второй случай (рис. 3-2, б): р<  . Общее количество работы, равное эксергии е, составит
. Общее количество работы, равное эксергии е, составит  . В зависимости от значений
. В зависимости от значений  и
и  величина е может быть как положительной, так и отрицательной или равной нулю (при
величина е может быть как положительной, так и отрицательной или равной нулю (при  ).
).
1 В качестве тела 3 может быть рассмотрен, например, груз, который способен перемещаться без трения по вертикали в поле тяготения.

Рис. 3-2. Термомеханическая система для определения эксергии рабочего тела,
а – при р >  ; б – при р<
; б – при р< 
Работа  представляет собой механическую составляющую эксергии (связанную с неравенством р ≠
представляет собой механическую составляющую эксергии (связанную с неравенством р ≠  ) и равна величине
) и равна величине
 (3-7)
(3-7)
где  − изотермический дроссель-эффект при
− изотермический дроссель-эффект при  в интервале давлений
в интервале давлений  .
.
Работа  представляет собой термическую составляющую эксергии (связанную с неравенством
представляет собой термическую составляющую эксергии (связанную с неравенством  ) и определяется уравнением
) и определяется уравнением
 (3-8)
(3-8)
Независимо от направления теплового потока q работа  всегда подводится к телу 3.
всегда подводится к телу 3.
Полная величина эксергии:
 (3-9)
(3-9)
Эксергия потока е может принимать все вещественные значения в интервале от -∞ до ∞.
Нулевая (химическая) эксергия
Нулевая экссргия е онеобходима в том случае, когда анализируемый процесс сопровождается изменением состава рабочего тела. Применительно к криогенной технике такое изменение состава возникает при низкотемпературном разделении смесей (системы класса D) и в тех случаях, когда эффекты смешения используются для внутреннего охлаждения (некоторые системы класса R).
В общем случае нулевая эксергия вещества определяется минимальной работой, необходимой для того, чтобы получить его из соответствующих веществ окружающей среды в чистом виде при давлении и температуре окружающей среды − «в нулевом состоянии».
Применительно к атмосферному воздуху получение каждого из его компонентов (О2, N2, Аr, Кr и т. д.) сводится к тому, чтобы сжать каждый из них от соответствующих парциальных давлений pi ( ) до
) до  .
.
* Здесь и в дальнейшем коэффициент Карно-  обозначается через
обозначается через  [5].
[5].
Формула (3-6) для этих условий примет вид:
 (3-10)
(3-10)
так как для любого компонента воздуха (который может рассматриваться как смесь идеальных газов) величина  .
.
Величина 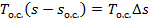 определяется изменением энтропии в процессе изотермического сжатия компонента i от парциального давления pi до давления
определяется изменением энтропии в процессе изотермического сжатия компонента i от парциального давления pi до давления  .
.
Знак минус перед величиной  в формуле (3-11) показывает, что работа затрачивается. Величина е обудет положительной, так как
в формуле (3-11) показывает, что работа затрачивается. Величина е обудет положительной, так как 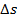 <0:
<0:
 . (3-11)
. (3-11)
Поскольку  , где
, где 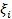 − мольная доля компонента в смеси, то нулевая эксергия будет равна:
− мольная доля компонента в смеси, то нулевая эксергия будет равна:
 (3-12)
(3-12)
Из формулы (3-12) следует, что нулевая эксергия тем больше, чем меньше мольная доля компонента в окружающей среде (в данном случае − воздухе).
В табл. 3-1 приведены подсчитанные по формуле (3-12) нулевые эксергии компонентов воздуха.
В системе, где отсутствует непосредственный материальный обмен с окружающей средой, нет необходимости подсчитывать полную нулевую эксергию.
Действительно, в этом случае за начало отсчета значений эксергии можно принять точку с параметрами  и
и  и составом рабочего тела в системе, не учитывая минимальную работу, которая требуется для получения этого вещества из окружающей среды. Например, в ожижителе водорода для точки, где эксергия равна нулю, может приниматься
и составом рабочего тела в системе, не учитывая минимальную работу, которая требуется для получения этого вещества из окружающей среды. Например, в ожижителе водорода для точки, где эксергия равна нулю, может приниматься  =293 К и
=293 К и  =0,1 МПа.
=0,1 МПа.
Таблица 3-1 Нулевая эксергия компонентов атмосферного воздуха
| Компоненты | e 0 | Компоненты | e 0 | ||
| кДж/м3 | кВт∙ч/м3 | кДж/м3 | кВт∙ч/м3 | ||
| Азот | 27,2 | 74,9 | Неон | ||
| Кислород | 170,6 | Криптон | |||
| Аргон | 508,4 | Ксенон |
Все энергетические превращения в системе, определяемые разностями эксергий, при этом будут правильно оценены. Работа, необходимая для получения водорода из веществ окружающей среды, определяемая его нулевой эксергией, из рассмотрения исключается, так как она не связана с работой криогенной системы L -ожижителя.
Если в системе происходят процессы смешения и разделения, то за точку начала отсчета эксергий принимается состояние смеси при  и
и  а эксергия ее фракций или чистых компонентов подсчитывастся с учетом работы их выделения из смеси.
а эксергия ее фракций или чистых компонентов подсчитывастся с учетом работы их выделения из смеси.