Понятие о коэффициенте полезного действия (к. п. д.) широко используется в термодинамике и связанных с ней инженерных науках, в частности низкотемпературной технике. Поскольку эта техника опирается, прежде всего, на термодинамику, мы будем рассматривать термин к. п. д. только в термодинамическом плане.
В этой области любой к. п. д. независимо от способа его определения можно назвать термодинамическим, поскольку его значение определяется через термодинамические функции состояния или параметры процесса 1.
Все многочисленные разновидности термодинамических к. п. д. могут быть по принципу их построения разделены на две группы.
К первой группе относятся те, которые представляют собой отношение полученного полезного эффекта А э к затратам А з (в термодинамическом смысле), необходимым в устройстве для получения этого эффекта:
. (3-32)
Такой принцип построения к. п. д. может быть назван прямым.
Ко второй группе относятся те, которые показывают отношение коэффициентов, характеризующих идеальный для данных условий процесс (или цикл) и соответствующий реальный процесс (или цикл).
Такой принцип вычисления к. п. д. может быть назван косвенным.
Для процессов, связанных с обратными циклами,
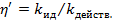(3-33)
Для процессов, связанных с прямыми циклами,
(3-33а)
Косвенное определение h по коэффициентам k ид и k действ из формул (3-33) и (3-33а) всегда сводится в конечном итоге к результату, получаемому по формуле (3-32).
Логика построения понятия к. п. д. как первой, так и второй группы требует, чтобы h не превышал единицы (или 100%), так как никакая система не может быть лучше идеальной и не может давать энергетический эффект, превышающий затраты энергии. При нарушении этого условия значение к. п. д. как показателя термодинамического совершенства системы утрачивается.
Все количественные и качественные особенности различных к. п. д., относящихся как к первой, так и ко второй группе, определяются тем, как выбираются величины 
и А зили коэффициенты, входящие в числитель и знаменатель формул (3-33) и (3-33а).
В выражения к. п. д., составленные на основе уравнения (3-2), входят качественно различные величины (например, тепловые потоки при разных температурах и работа), выбранные независимо от их знака.
1 Применение термина «термодинамический к. п. д.» к отдельным, частным видам к. п. д. неоправданно, поскольку не дает никакой информации об особенностях данного к. п. д.
Из таких величин для низкотемпературной техники представляет интерес только одна − холодильный коэффициент e:
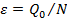(3-34)
где Q 0 − полученный холод, a N − затраченная мощность.
Коэффициент e может быть как меньше, так и больше единицы, а значение величины Q о.c(тепло, отводимое в окружающую среду), рассматриваемое как потеря, больше Q 0, поскольку 
.
Таким образом, эффект, получаемый от холодильной установки, может быть больше, чем затраты, а потеря всегда больше, чем получаемый эффект. Такой результат несколько противоречит представлению о к. п. д., поэтому величину e обычно называют не к. п. д., а холодильным коэффициентом.
Если действие низкотемпературной установки обеспечивается не посредством работы, а тепловым потоком Q (например, в абсорбционных холодильных установках или криорефрижераторах с тепловым приводом), то эффективность будет определяться отношением
, (3-35)
которое, также может быть больше единицы. Этот коэффициент называется коэффициентом преобразования. Все сказанное относительно е относится и к 
.
На практике часто используется еще один вид к. п. д., относящийся исключительно к процессам теплообмена. Этот к. п. д. равен отношению тепла 
, получаемого одним потоком рабочего тела, к теплу 
, отдаваемому другим потоком:
. (3-36)
На первый взгляд величина h в формуле (3-36) удовлетворяет требованию 
Однако это условие выдерживается только в частном случае, при Т>Т о.с.. При Т<Т о.с, т. е. в области низкотемпературной техники, значение 
и h >1, поскольку тепловой поток через изоляцию направлен от окружающей среды к рабочему телу. Чем хуже тепловая изоляция, тем выше будет величина h. Поэтому к. п. д. по формуле (3-36) также не имеет общего значения.
Если использовать для подсчета к. п. д. эксергетические величины, то, напротив, качественное различие потоков энергии учитывается в полной мере тем, что составляющие баланса уже заранее изменены так, чтобы отразить это различие 1.
1 При пересчете величин энергии в величины эксергии.
Применение величин Е для составления к. п. д. позволяет при использовании как формулы (3-32), так и (3-33) или (3-33а) эти противоречия исключить. Во всех случаях будут получены одни и те же конечные результаты.
Определение к. п. д. по эксергетическому балансу системы основано на уравнениях (3-4) и (3-32). Независимо от вида системы и характера проходящего в ней процесса величины А эи А зкачественно однородны.
В соответствии с условиями эксергетического баланса в А эвключаются только такие потоки эксергии, сумма или разность которых определяетполучаемый эффект, а в A з− те, сумма или разность которыхопределяет затраты.
Величина А эпо существу представляет собой эксергетическую производительность 
.
Если затраты А з и эффект процесса отнести ко времени и выразить в единицах мощности, то
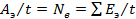. (3-37)
В соответствии с формулой (3-4) *
.
Для идеального процесса, где потери D отсутствуют,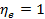 
, или 100%. Если подведенная эксергия полностью теряется в процессе, то он полностьюнеобратим и в этом случае 
.
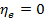В реальных процессах, которые только частично обратимы, 
, поскольку отведенная эксергия может быть использована для возвращения части затраченной энергии. Чем выше значение 
, тем система термодинамически совершеннее.
Подведенная к системе или ее части 
и отведенная от нее 
эксергия может быть подсчитана двумя способами.
В первом случае в величину 
включаются полностью все виды подведенной эксергии независимо от того, претерпевают они изменения в системе или нет. Точно так же подсчитывается значение . Полученный к. п. д. обозначим 
Во втором случае в величину включается только та часть подведенной эксергии, которая в пределах рассматриваемой системы:
переходит в другой вид эксергии;
передается от одного рабочего тела к другому;
теряется вследствие необратимости.
* Величина 
(сумма эксергии затрат) определяется аналогично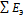 
как сумма или разность потоков эксергии, определяющая затраты.
Соответственно в величину 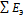включается та часть отводимой эксергии, которая получена либо из других ее видов, либо от другого рабочего тела. Полученный к. п. д. обозначим 
.
Разница между двумя описанными способами расчета величин 
и 
заключается в том, что при подсчете по второму способу эксергия, не претерпевающая в системе превращений, а просто «протекающая» через нее, исключается из рассмотрения 1. Поэтому и числитель и знаменатель формулы для к. п. д. уменьшаются на одну и ту же величину С, и в общем случае 
. При этом:
1)крайние значения величин к. п. д. (0 и 1) не изменяются, при 
, а при 
, или 100%;
2) величина потерь 
не изменяется, так как из обеих величин вычитается одна и та же постоянная С;
3) коэффициент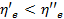 
везде, за исключением начальной и конечной точек, и эта разница тем больше, чем больше значение С.
Перечисленные свойства и показывают, что оба эти вида к. п. д. одинаково удовлетворяют требованиям, предъявляемым к величине к. п. д.
При анализе большинства низкотемпературных систем применимы оба способа подсчета к. п. д.; выбор того или иного способа производится в зависимости от конкретных условий.
В некоторых системах второй способ неприменим, так как в них либо невозможно разделить эксергию и выделить потоки, не входящие в , либо такие потоки вообще отсутствуют.
Во всех процессах, где происходит преобразование одного вида эксергии в другой в пределах изменения параметров одного рабочего тела, использование первого способа хотя и допустимо, но носит формальный характер. Действительно, при таком подходе процессы преобразования эксергии одного вида (например, ep) в эксергию другого вида (например, eT) выпадают из рассмотрения. При втором способе оценки к. п. д. эффективность преобразования эксергии в пределах одного и того же рабочего тела может быть оценена (например, при низкотемпературном дросселировании).
Рассмотрим примеры определения .
Холодильная установка или криорефрижератор (класс R). В этом случае содержанием величины будет эксергетическая холодопроизводителыюсть 
, а затрат 
. Тепловой поток Q o.c., отведенный при T o.с. в окружающую среду, в баланс не входит, так как его эксергия равна нулю.
1 По предложению проф. Г. Н. Костенко эту эксергию иногда называют «транзитной».
Поэтому
(3-38)
Здесь 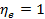в идеальном случае, когда 
и 
.
Связь между и холодильным коэффициентом e можно установить, сопоставив уравнения (3-38) и (3-34):
(3-39)
Холодильный коэффициент представляет собой функцию двух независимых переменных, одна из которых определяет совершенство системы, а другая зависит только от температурных условий.
Так как 
, а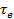 
в низкотемпературной области меняется от 0 до -∞, то холодильный коэффициент может быть как больше, так и меньше единицы, и не связан непосредственно с совершенством установки. Поэтому e может быть больше у менее совершенной системы. Напротив, эксергетический к. п. д. характеризует, как и во всех других случаях, совершенство установки однозначно, независимо от температурных условий.
Коэффициент полезного действия рефрижератора может быть определен и косвенно − по отношению холодильных коэффициентов действительной и идеальной установок по формуле (3-33).
Для этого случая
Отсюда
Следовательно, и в процессе 
к. п. д., выведенный на основе общих правил, является мерой термодинамического совершенства системы.
Если установка работает за счет теплового потока Q, а не мощности N, то ее к. п. д. определяется тем же путем, но А збудет равно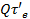 
. Поэтому
(3-40)
В общем случае величина любой энергетической характеристики h,составленной на основе уравнения энергетического баланса для стационарных процессов взаимного преобразования тепла и работы 
или трансформации тепла 
, будет функцией двух независимых переменных − и *:
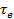(3-41)
Определение к.п.д. процесса теплообмена по первому началу может привести, как уже указывалось выше, к значению 
по формуле (3-2) при T < Т о.с, поскольку в результате теплопритоков извне нагревающийся поток получит больше тепла 
, чем отдает охлаждающийся 
. Это противоречие легко устраняется при использовании эксергетического к. п. д. . В самом деле, учитывая, что 
, а 
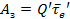, получаем:
(3-42)
или, поскольку для изобарного процесса 
**,
(3-42а)
Теплообмен через изоляцию с окружающей средой при Т<Т o.с.приводит всегда к уменьшению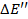 
. Поэтому всегда меньше единицы.