А) ОСОБЕННОСТИ ЭКСЕРГЕТИЧЕСКИХ ДИАГРАММ

Широкое использование понятия эксергии в термодинамике, и в частности при термодинамическом анализе, привело к необходимости непосредственно, без специальных расчетов, находить величины е, e_q и их составляющие для различных веществ и смесей, а также значения t_e при заданных Т и .

Решение этих задач, так же как и многие расчеты с эксергстическими функциями, удобно проводить графическими методами.

В некоторых случаях для этого можно использовать диаграммы состояния соответствующих веществ в координатах Т, s и особенно h, s, нанеся на них линии e =const. Однако такой метод не всегда позволяет получить все необходимые данные. Поэтому были разработаны и применяются на практике специальные диаграммы, в которых эксергетические функции используются непосредственно в качестве одной из координат, а также номограммы с эксергией е в качестве ординаты. Наиболее практически важная из таких номограмм предназначена для определения и изотермической работы сжатия различных газов в широком интервале температур и давлений [42].

Посредством эксергетических диаграмм могут быть также выявлены и наглядно представлены такие свойства и характеристики процессов, которые не могут быть получены с помощью обычных диаграмм состояния, в которые параметры окружающей среды не входят.

Рассмотрим свойства некоторых эксергетических диаграмм состояния, а также методы их использования для термодинамических расчетов низкотемпературных процессов.

б) е, h -ДИАГРАММА (ЭКСЕРГИЯ − ЭНТАЛЬПИЯ) И ЕЕ МОДИФИКАЦИИ

Диаграмма е, h представляет собой косоугольную модификацию h, s -диаграммы, где ось энтропии наклонена влево от вертикали на угол, при котором все прямые e =const располагаются горизонтально.

В зависимости от физических свойств вещества расположение его л граммы на координатной сетке е, i выглядит различно. На рис. 3-4 показан внешний вид диаграммы для двух характерных случаев.

В первом случае (рис. 3-4, а), характерном для криоагентов, нулевая точка определяется пересечением изобары р ₀.с и изотермы ,находящейся в области перегретого пара (газа). Поэтому область влажного пара, температура в которой значительно ниже ,соответствует состояниям с высокой эксергией и перемещается в левый верхний край диа граммы.

Рис. 3-4. Внешний вид е, h -диаграммы для разных веществ.

Чем ниже критическая температура рабочего тела, тем, при прочих равных условиях, выше эксергня влажного пара и жидкости и тем выше расположена область влажного пара. Такой вид имеют диаграммы метана, воздуха, кислорода, азота, водорода, неона, гелия и др. Во втором случае (рис. 3-4, б) прямая окружающей среды совпадает с изотермой в области влажного пара. Это характерно для таких ве ществ, как вода и ряд хладоагентов с нормальной температурой кипения T _нк ниже 250−260 К (в частности, аммиак и большинство фреонов). Подробный анализ свойств е, h- диаграммы дан в [5].

Определение составляющих величин эксергии

Диаграмма e, h позволяет определить для любого состояния вещеества составляющие эксергии потока, связанные как с разностью давлении e_p, так и с разностью температур e_T по отношению к окружающей среде.

Нужное для определения составляющих е_р и e_T построение показано на рис. 3-5. Например, для точки 1 величина будет равна разности ординат точек 1 и 2 (точка 2 находится на пересечении изобары р ₁и изотермы );величина равна разности ординат точек 2 и 0.

Все состояния, соответствующие прямой ab,имеют одинаковую эксергию e ₁. Поэтому обратимый переход из любого заданного состоянии на этой прямой в другое, определяемое этой же ординатой е ₁возможен без затраты работы (и без ее получения). При этом только изменяется соотношение между e_T и e_p; один вид эксергии, связанный с , переходит в другой, связанный с или наоборот.

Рис. 3-5. Графическое определение составляющих эксергии e_p и e_T.

 

В частности, в точке 1 ' значение e_T =0 и e=e_p. В точке 1",напротив, e_p =0, а e=e_T.

Взаимосвязь различных состояний с точки зрения условий перехода одного в другое наглядно иллюстрируется на e, h -диаграмме посредством простой механической аналогии.

Можно представить себе прямую, соединяющую две точки, как след плоскости, перпендикулярной плоскости диаграммы. Тогда шарик, помещённый на этой плоскости, будет скатываться в сторону возможного направления процесса. Работа, которую в этом случае можно получить от единицы массы вещества − D e, равна изменению потенциальной энергии единицы массы шарика, если рассматривать величину е как высоту, определяющую его положение.

Для состояний, расположенных на прямой ab, значение D e = 0 и шарик А может передвигаться в любую сторону без затраты или производства работы.

Если рассмотреть состояния, точки которых расположены на прямой то видно, что шарик Б может скатываться только в направлении от а к с. Это означает, что самопроизвольный переход по этой прямой возможен только вправо вниз; движение в противоположном направлении возможно только при затрате работы l (или соответствующей эксергии любого вида), в идеальном случае равной D e, в реальном – большей D e на величину потерь d.

За счет эксергии самого рабочего тела такой процесс (с движением вверх) неосуществим.

В точках 5 и 6 значения e_p и e_T соответственно равны по абсолютной величине и противоположны по знаку; поэтому значения e ₅ и e ₆ равны нулю. В точках 4 и 3 значение e <0.

Процессы перевода одного вида эксергии в другой в потоке рабочего тела широко используются в технике как в одном потоке, так и при взаимодействии нескольких потоков. Примером первого процесса могут служить дросселирование и расширение с отдачей внешней работы, используемые в низкотемпературной технике, когда за счет уменьшения e_p увеличивается e_T (связанная с внутренним охлаждением газа)¹. Примером второго вида является процесс в эжекторе, где за счет уменьшения одного потока возрастает другого потока при соответствующем изменении e_T.

Поскольку реальные процессы связаны с потерями эксергии, суммарная величина на выходе всегда меньше, чем на входе, на величину потери d.

¹ Этот вопрос подробно рассмотрен в гл. 4.

WQ

Расчеты работы и эксергии тепла в обратимых процессах посредством е, h -диаграммы

Диаграмма е, h позволяет найти работу и некоторые другие энергетические характеристики процессов, проводимых с реальными рабочими телами¹. Без использования е, h -диаграммы такие расчеты обычно требуют проведения специальных вычислений. Рассмотрим некоторые характерные примеры.

Сжатие и расширение любого рабочего тела при обратимом проведении процесса может характеризоваться энергетическим и эксергетическим балансами. Поскольку при сжатии и расширении изменяются только знаки, а уравнения остаются теми же, мы рассмотрим в качестве примера процесс сжатия, схема которого показана на рис. 3-6.

Пользуясь первым началом термодинамики и уравнением (3-3а) и принимая во внимание, что D =0 и D E= 0 (процесс обратимый и стационарный), получим следующие уравнения.

Уравнение энергетического баланса (рис. 3-6, а) для единицы массы рабочего тела:

(3-20)

или

(3-21)

Естественно, что все полученные ниже выводы относятся и к идеальному газу как к частному случаю.

 

Рис. 3-6. Энергетический и эксергетичеекий балансы процессов идеального
изотермического сжатия.

а − энергетический баланс; б− эксергетический баланс.

Уравнение эксергетического баланса (рис. 3-6, б):

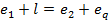
или

(3-22)

В зависимости от знака 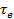, определяемого соотношением температур Т и ,величина 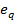может быть как положительной, так и отрицательной. Практически наиболее интересен случай сжатия при Т= . В этом случае и . Следовательно,

(3-23)

т. е. работа изотермического сжатия (расширения) при температуре окружающей среды равна разности эксергий в начальном и конечном состояниях.

На рис. 3-7 показан такой изотермический процесс сжатия в координатах е, h. На практике наиболее просто определить изотермическую работу сжатия (расширения) по специальным эксергетическим номограммам, построенным для разных газов (воздуха, кислорода, аргона, in порода и гелия) [42].

Расчет работы изотермического сжатия по аналитическим формулам, особенно с учетом реальности газа, намного более трудоемок.

В научной и технической литературе часто можно встретить термин «энергия сжатого газа» и связанные с ним такие формулировки, как «использование энергии сжатого газа», «потери энергии сжатого газа» и т. д.

Рис. 3-7. Процесс изотермического сжатия при Т= в е, h -диаграмме.

Рис. 3-8. Поверхности состояний бинарной смеси в пространстве h, e,𝜉.

Такая терминология не соответствует действительной картине энергетических превращений при сжатии ирасширении газа,поскольку энергия сжатого газа незначительно или совсем не отличается от энергии несжатого газа и в большинстве случаев меньше ее (в частности, длявоздуха) [5]. Следовательно, речь должна идти не об энергии сжатого газа, а об его эксергии, которая и определяет его работоспособность.

Точно так же неверно говорить о «потере энергии» при дросселировании газа (в клапанах, дроссельных устройствах и т. д.). В этом случае речь должнаидти о потерях эксергии,величина которыхдействительно отражает физическую сущность процесса.

В тех случаях, когда изотермическое сжатие происходит при температуре T ≠ , значение 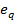не равно нулю и работа отличается от D e [5].

Диаграмма е, h позволяет определять и минимальную работу любых других процессов изменения состояния, например процессов охлаждения.

Найдем, например, пользуясь e, h -диаграммой воздуха [5, 43] величину минимальной работы, необходимой дляперевода воздуха из нулевого состояния в жидкость при р= 0,1МПа. Эксергия жидкости при р = 0,1 МПа е =702,5 кДж/кг. Следовательно, l = 702,5−0=702,5 кДж/кг.

Если бы воздух был предварительно охлажден, например до 150 К, то его эксергия в начальной точке процесса составила бы 53,5 кДж/кг. Тогда необходимая минимальная работа была бы равна

Аналогично описанным примерам, по разности эксергии можно определить минимальную (или максимальную) работу перехода вещества из любого заданного состояния в другое. е, h -диаграмма дает возможность производить также и расчеты, связанные с теплообменом (гл. 4).

Пользуясь зависимостью (3-19) между эксергией тепла 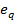и разностью эксергии в изобарном процессе, можно найти 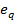для любого изменения состояния при p =const. Найдем, например, эксергию теплового потока, который нужно отвести от потока воздуха при р =6,0 МПа, чтобы охладить его от 300 до 160 К. Эксергия воздуха при 300 К и 6,0 МПа e ₁=343 кДж/кг и при 160 К e ₂=409 кДж/кг. Следовательно, . Количество тепла, отводимого от газа, равно разности энтальпий кДж/кг. Таким образом, отводу тепла от рабочего тела при T < соответствует подвод эксергии.

в) ДИАГРАММА (ЭКСЕРГИЯ −КОНЦЕНТРАЦИЯ)

В низкотемпературной технике часто приходится встречаться с раз­делением смесей, в частности двухкомпопентных (бинарных). Процес­сы с двухкомпонептными смесями обычно исследуются посредством

I -диаграммы (энтальпия − концентрация) и -диаграммы (энтро­пия− концентрация); последняя позволяет находить лриращеняя эн-ропии, а по ним − работу разделения и потери от необратимости. Эк-п'ргетические диаграммы позволяют определять и эксергии компонен­тов смеси и работу разделения непосредственно.

Для этого необходимо располагать значениями е не только для различных давлений и температур, но и в зависимости от концентрации. Соответствующая эксергетическая диаграмма должна отличаться от е₉ /-диаграммы наличием третьей координаты ^-концентрации¹.

Состояние смеси будет при этом отображаться точками в простран­стве . Условиям фазовых переходов (х=0 и х=1, где х − влаж­ность пара), а также p=const и r=const будут соответствовать опре­деленные поверхности. Линии пересечения этих поверхностей с плоско­стью дадут е, г-диатрамму для смеси соответствующего состава.

При получится е> /-диаграмма чистого вещества В, при −

чистого вещества А (рис. 3-8),

¹ Для смеси, состоящей из легкокипящего компонента А и тяжелокипящего В_у личина показывает мольную концентрацию легкокипящего компонента Л.

Рис. 3-9. Схема -диаграммы для давления ро.с

Рис. 3-10. Влияние изменения давления на положение изотерм в диаграмме.

 

Проекции линий пересечений поверхностей 7*=const дают на плос­костях и s- и -диаграммы для данных давлений р.

Диаграмма широко известна и применяется в расчетах с бинар­ными смесями. Диаграмма _ используется для термодинамического анализа процессов с бинарными смесями, так же как и е, i-диаграмма для процессов с чистым веществом.

На рис. 3-9 показана схема -диаграммы для давления р=р₀._с.

По внешнему виду -диаграмма напоминает -диаграмму, но для вещества с пограничные кривые в области влажного пара,

так же как и изотермы при , расположены в обратном порядке:

изотермы, относящиеся к более низким температурам, находятся выше. Это объясняется тем, что е при и p=const растет в низкотемпе-

ратурной области по мере понижения энтальпии (как это видно и из i, е-диаграммы чистого вещества при p=const). В области изо-

термы также расположены выше изотермы 7₀.с, но эксергия в этой об­ласти растет с температурой. Во всех случаях соблюдается одно и то же правило; чем больше отличается температура от Т₀._с> тем дальше распо­ложена рассматриваемая изотерма от изотермы Г₀.с.

Концентрация соответствует составу разделяемой смеси. Для

воздуха, рассматриваемого как бинарная смесь кислорода и азота,. Точка ос нулевой эксергией соответствует давлению р₀.с и тем­пературе Го.с. Для других смесей выбор точки о определяется, как ука­зывалось выше, составом разделяемой смеси и параметрами р₀.с и Го.с-

Все изотермы на -диаграмме обращены выпуклостью вниз, так как эксергия чистых компонентов выше эксергии смесей на величину минимальной работы разделения.

В верхней части диаграммы находится область влажного пара, при­чем линия х=0 лежит выше, чем линия х=\. Это объясняется большим значением эксергии жидкости для любой данной , чем сухого насыщен­ного пара. В области влажного пара изотермы представляют собой наклонные прямые, причем угол их наклона изменяется по мере прибли­жения к линиям и , где изотермы вертикальны, как и в -диа­грамме.

При давлении р<р₀.с (вакуум) изотерма Г₀.с опускается частично или полностью под прямую <? = 0, в область е<0. Соответственно сме­щаются вниз и другие изотермы. Границы области влажного пара при этом раздвигаются вследствие увеличения разности е при х==0 и х*=1 для всех значений концентраций (рис. 3-10). При давлении р>ро.с изо­термы смещаются вверх, а область влажного пара сужается.

На -диаграмму можно нанести изотермы и пограничные кривые для любых нужных давлений. Тогда, пользуясь свойствами эксергети- ческой диаграммы, можно определить минимальную работу разделения для любых состояний продуктов разделения, с учетом их температур и давлений. Действительно, работа разделения равна сумме работ изотер*

мического сжатия компонентов от их парциальных давлений pi до исход­ного давления смеси р. (Для иеидеальных смесей в выражение для ми­нимальной работы разделения смеси идеальных газов при Т₀._с и р₀._с следует вместо парциального давления подставлять летучесть соответ­ствующих компонентов). Каждая из полученных при расчете работ рав­на соответствующей величине , которую легко найти на -диаграм­ме путем простого построения.

Таким образом, посредством -диаграммы можно находить мини­мальную работу процессов, включающих одновременно как разделение-смеси, так и изменение любых параметров исходной смеси и продуктов разделения.

Подробно свойства -диаграммы и методика расчетов с ее ис-

пользованием изложены в [5].

г) -ДИАГРАММА (ЭНТАЛЬПИЯ − ЭКСЕРГЕТИЧЕСКАЯ ТЕМПЕРАТУРА)

Диаграмма представляет собой модификацию U ^-диаграммы,,

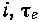широко применяемой в низкотемпературной технике. Разница между этими диаграммами состоит в том, что по оси ординат откладывается не температура (К), а величины функции . Так как каждому значению Т соответствует при данном Т₀.с определенное значение , то изотермы на -диаграмме проходят горизонтально.

Диаграмма 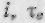позволяет проводить расчеты, связанные с эксер-

гией теплового потока . Значение эксергии теплового потока = = , связанного с изобарным изменением состояния, изображается

па 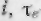-диаграмме заштрихованной площадью (рис. 3-11). Действитель­но, в элементарном изобарном процессе аЬ отрезок оси абсцисс di равен элементарному количеству тепла, отданному или полученному телом. Поэтому площадь элементарной площадки abed, высота которой рав­на т_е, численно равна 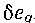_, Соответственно для всего процесса 1-2 пло­щадь равна:

В расчетной практике и при термодинамическом анализе наиболь­шее распространение получили графики в -координатах, в которых использованы свойства -диаграммы, описанные выше. Основным отличием такого графика от -диаграммы является то, что по оси абсцисс откладывается не параметр состояния £, а параметр процесса», сопровождающегося передачей эксергии в форме тепла q. Поэтому диа­грамма становится пригодной для изучения процессов теплообмена, где количества и составы веществ, участвующих в процессах, различны и величина i одного вещества недостаточна для тепловой характеристи­ки процесса. На графике можно наносить кривые, характеризующие из­менение температуры и тепловые потоки разных веществ при разных количествах их в потоках, q, т_с-диаграмма может использоваться для графического анализа процессов теплообмена. Способ изображения

эксергии тепла на -диаграмме ничем не отличается от описанного

выше для 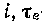-диаграммы. Это позволяет наглядно изобразить изменение эксергии тепла при теплообмене.

Рассмотрим для примера теплообменник, работающий при темпе­ратурах ниже То.с- Откладывая по оси q на -диаграмме количество тепла, переданное в данном теплообменнике (отрезок на рис. 3-12), а на вертикальных линиях, проходящих через эти точки, − значения т_е, по­лучим кривые, показывающие изменение температуры каждого из пото­ков по мере отвода или подвода тепла *.

Охлаждаемому телу А будет соответствовать кривая 1-2, нагревае­мому В − кривая 3-4. Так как во всех сечениях теплообменника имеется конечная разность температур, то кривая 3-4 везде будет проходить ниже кривой 1-2. По смыслу диаграмм i,x_e или q,x_e, площадь a-S-4-b − отри­цательна и соответствует эксергии, отведенной от тела В. Площадь l-2-a-b положительна и равна эксергии, полученной телом А. Разность между ними − площадь 1-2-3-4 − равна эксергии d, потерянной при теп­лопередаче.

Таким образом, -диаграмма позволяет показать численное зна-

чение потерь от необратимости при теплообмене и распределение их вдоль аппарата.

¹ Точки для построения этих кривых удобнее всего брать с • или t, Г-диаграм-мы соответствующего вещества.

Рис. 3-11. Величина эксергии теплового потока на -диаграмме.

Рис. 3-12. Определение потерь в процессе теплообмена по -диаграмме.