План лекции
1. Геометрический смысл производной.
2. Дифференциал функции и его свойства.
3. Экстремумы функции.
4. Теорема Ферма.
· Геометрический смысл производной.
Производная в точке  равна угловому коэффициенту касательной к графику функции
равна угловому коэффициенту касательной к графику функции  в этой точке.
в этой точке.
рассмотрим график функции  :
:
из рисунка видно, что для любых двух точек  графика функции:
графика функции:
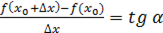
где  - угол наклона секущей
- угол наклона секущей  .
.
Таким образом, разностное отношение равно угловому коэффициенту секущей.
Если зафиксировать точку  и двигать по направлению к ней точку
и двигать по направлению к ней точку  , то
, то  неограниченно уменьшается и приближается к 0, а секущая
неограниченно уменьшается и приближается к 0, а секущая 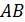 приближается к касательной
приближается к касательной 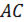 .
.
Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке  .
.
Отсюда следует:
Производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

Тогда уравнение касательной к кривой  в точке
в точке 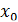 имеет вид:
имеет вид:


Пример:
Составить уравнение касательной к кривой 
Решение:
Найдем производную в точке 

Уравнение касательной имеет вид:

· Дифференциал функции и его свойства
Линейную функцию  называют дифференциалом функции
называют дифференциалом функции  в точке и обозначают
в точке и обозначают  . Для функции
. Для функции  производная в каждой точке
производная в каждой точке 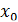 равна 1, то есть
равна 1, то есть  . Поэтому пишут:
. Поэтому пишут:

Приближенное значение функции вблизи точки  равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом:
равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом:

Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.
Геометрически дифференциал функции  – это приращение ординаты касательной к графику функции в данной точке при изменении абсциссы точки на
– это приращение ординаты касательной к графику функции в данной точке при изменении абсциссы точки на  .
.
· Экстремумы функции
Экстремум — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Определения:


Замечание:


· Теорема Ферма
Лемма Ферма утверждает, что производная дифференцируемой функции в точке локального экстремума равна нулю.
Замечание:
Производная дифференцируемой функции в точке локального экстремума равна нулю. Её касательная в этой точке параллельна оси абсцисс. Обратное, вообще говоря, неверно.

Примеры:


Контрольные вопросы:
1. Сформулировать геометрический смысл производной.
2. Написать уравнение касательной к кривой.
3. Что такое дифференциал функции?
4. Дать определения экстремуму, точке экстремума, точке минимума, точке максимума.
5. Сформулировать теорему (лемму) Ферма.
ЛЕКЦИЯ 6:
Возрастание и убывание функции
План лекции
1. Теорема Ролля, Лагранжа, Коши.
2. Возрастание и убывание функции.
3. Достаточные условия экстремума.
4. Примеры практических задач на экстремум.
· Теорема Ролля (теорема о нуле производной) утверждает, что
Если вещественная функция, непрерывная на отрезке  и дифференцируемая на интервале
и дифференцируемая на интервале  , принимает на концах этого интервала одинаковые значения, то на этом интервале найдется, хотя бы одна точка, в которой производная функции равна нулю.
, принимает на концах этого интервала одинаковые значения, то на этом интервале найдется, хотя бы одна точка, в которой производная функции равна нулю.
1. Доказательство:
Если функция на отрезке постоянна, то утверждение очевидно, поскольку производная функции равна нулю в любой точке интервала.
Если же нет, поскольку значения функции в граничных точках сегмента равны, то согласно теореме Вейерштрасса (в математическом анализе и общей топологии) гласит, что функция, непрерывная на компакте, ограничена на нём и достигает своей верхней и нижней грани), она принимает своё наибольшее или наименьшее значение в некоторой точке интервала, то есть имеет в этой точке локальный экстремум, и по лемме Ферма, в этой точке производная равна 0.
2. Геометрический смысл теоремы Ролля:
 Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.
Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.
3. Следствие:
Если непрерывная функция обращается в ноль в  различных точках, то ее производная обращается в ноль, по крайней мере, в
различных точках, то ее производная обращается в ноль, по крайней мере, в  различных точках, причем эти нули производной лежат в выпуклой оболочке нулей исходной функции. Это следствие легко проверяется для случая действительных корней, однако имеет место и в комплексном случае.
различных точках, причем эти нули производной лежат в выпуклой оболочке нулей исходной функции. Это следствие легко проверяется для случая действительных корней, однако имеет место и в комплексном случае.
· Формула конечных приращений или теорема Лагранжа о среднем значении утверждает, что:
если функция 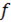 непрерывна на отрезке
непрерывна на отрезке  и дифференцируема в интервале
и дифференцируема в интервале 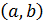 , то найдётся такая точка
, то найдётся такая точка 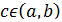 , что
, что 
Геометрически это можно переформулировать так:
на отрезке  найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Механическое истолкование:
Пусть  расстояние точки в момент
расстояние точки в момент  от начального положения. Тогда
от начального положения. Тогда  есть путь, пройденный с момента
есть путь, пройденный с момента  до момента
до момента 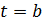 , отношение
, отношение  средняя скорость за этот промежуток. Значит, если скорость тела определена в любой момент времени
средняя скорость за этот промежуток. Значит, если скорость тела определена в любой момент времени  , то в некоторый момент она будет равна своему среднему значению на этом участке.
, то в некоторый момент она будет равна своему среднему значению на этом участке.
Доказательство:

· Теорема Коши о среднем значении


Геометрически это можно переформулировать так:
Если 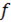 и
и  задают закон движения на плоскости (то есть определяют абсциссу и ординату через параметр
задают закон движения на плоскости (то есть определяют абсциссу и ординату через параметр  ), то на любом отрезке такой кривой, заданном параметрами
), то на любом отрезке такой кривой, заданном параметрами  и
и  , найдётся касательный вектор, коллинеарный вектору перемещения от
, найдётся касательный вектор, коллинеарный вектору перемещения от  до
до  .
.
Доказательство:
Для доказательства введем функцию:

Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны  . Воспользовавшись упомянутой теоремой, получим, что существует точка
. Воспользовавшись упомянутой теоремой, получим, что существует точка  , в которой производная функции
, в которой производная функции  равна нулю, а
равна нулю, а 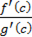 равна как раз необходимому числу.
равна как раз необходимому числу.
· Возрастание и убывание функции
Функция  называется возрастающей на отрезке [a, b], если для любой пары точек
называется возрастающей на отрезке [a, b], если для любой пары точек  ,
,
 выполняется неравенство
выполняется неравенство  , и строго возрастающей — если выполняется неравенство
, и строго возрастающей — если выполняется неравенство  . Аналогично определяется убывание и строгое убывание функции.
. Аналогично определяется убывание и строгое убывание функции.
Например, функция  (рис., а) строго возрастает на отрезке [0,1], а
(рис., а) строго возрастает на отрезке [0,1], а  (рис., б) строго убывает на этом отрезке.
(рис., б) строго убывает на этом отрезке.
Возрастающие функции обозначаются  ↑, а убывающие
↑, а убывающие 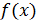 ↓. Для того чтобы дифференцируемая функция
↓. Для того чтобы дифференцируемая функция 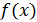 была возрастающей на отрезке
была возрастающей на отрезке  , необходимо и достаточно, чтобы её производная
, необходимо и достаточно, чтобы её производная  была неотрицательной на
была неотрицательной на  .
.
Наряду с возрастанием и убыванием функции на отрезке рассматривают возрастание и убывание функции в точке. Функция  называется возрастающей в точке
называется возрастающей в точке  , если найдётся такой интервал
, если найдётся такой интервал  , содержащий точку
, содержащий точку  , что для любой точки
, что для любой точки  из
из  ,выполняется неравенство
,выполняется неравенство  , и для любой точки
, и для любой точки  из
из  , выполняется неравенство
, выполняется неравенство
 .
.
Аналогично определяется строгое возрастание функции в точке  .
.
Если  , то функция
, то функция  строго возрастает в точке
строго возрастает в точке  . Если
. Если  возрастает в каждой точке интервала (a, b), то она возрастает на этом интервале.
возрастает в каждой точке интервала (a, b), то она возрастает на этом интервале.

· Достаточные условия экстремума функции.
Пусть функция f (x) определена всюду в некоторой окрестности точки C. Говорят, что функция f (x) имеет в точке C локальный максимум (минимум), если существует такая окрестность точки C, в пределах которой значение f (с) является наибольшим (наименьшим).
Локальный максимум и минимум объединяются общим названием экстремум.
1) Первое достаточное условие экстремума.
Теорема 1.
Пусть
- точка C является точкой возможного экстремума функции f (x),
- f (x) дифференцируема всюду в некоторой окрестности точки C.
Тогда, если в пределах указанной окрестности  слева от точки C и
слева от точки C и  справа от точки C, то функция f (x) имеет в точке C локальный максимум (минимум). Если же f’ (x) имеет один и тот же знак слева и справа от точки C, то экстремума в точке C нет.
справа от точки C, то функция f (x) имеет в точке C локальный максимум (минимум). Если же f’ (x) имеет один и тот же знак слева и справа от точки C, то экстремума в точке C нет.
Доказательство.
1). Пусть  слева от точки с и
слева от точки с и  справа от C. Обозначим x 0 ¹ c любое значение аргумента из рассматриваемой окрестности. Достаточно доказать, что
справа от C. Обозначим x 0 ¹ c любое значение аргумента из рассматриваемой окрестности. Достаточно доказать, что

Функция f (x) дифференцируема (а, следовательно, непрерывна) на сегменте  . По формуле Лагранжа (формула конечных приращений)
. По формуле Лагранжа (формула конечных приращений)

где C лежит между b и a. Т.к.  при
при  и
и  при
при 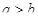 , то правая часть положительна (отрицательна).
, то правая часть положительна (отрицательна).
2). Пусть теперь f’ (x) имеет один и тот же знак слева и справа от C. Обозначая через x 0 любое значение аргумента, отличное от C, и повторяя проведенные выше рассуждения, мы докажем, что правая часть имеет разные знаки слева и справа от C. Это доказывает отсутствие экстремума в точке C.
Теорема доказана.
Вытекающее из Теоремы 1. правило
1). Если при переходе через данную точку с возможного экстремума производная f’ (x) меняет знак с плюса на минус (с минуса на плюс), то функция f (x) имеет в точке с локальный максимум (минимум).
2). Если же при переходе через данную точку с возможного экстремума производная f’ (x) не меняет знака, то экстремума в точке с нет.
Пример.

 , x = 2 – точка возможного экстремума. Т.к.
, x = 2 – точка возможного экстремума. Т.к.  как слева, так и справа от
как слева, так и справа от
x = 2, то экстремума в этой точке нет.
2) Второе достаточное условие экстремума.
Теорема 2.
Пусть функция f (x) имеет в данной точке с возможного экстремума конечную вторую производную.
Тогда f (x) имеет в точке с максимум, если  , и минимум, если
, и минимум, если  .
.
Доказательство.
Из условия 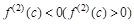 и из Теоремы
и из Теоремы
(Теорема: Если функция f (x) дифференцируема в точке с и  , то эта функция возрастает (убывает) в точке C.)
, то эта функция возрастает (убывает) в точке C.)
вытекает, что f’ (x) убывает (возрастает) в точке C. Поскольку по условию f’ (с) = 0, то найдется такая окрестность точки C, в пределах которой  слева от C и
слева от C и  справа от C.
справа от C.
Тогда по Теореме 1 f (x) имеет в точке с максимум (минимум).
Теорема доказана.
Замечание.
Теорема 2 имеет более узкую сферу действия, чем Теорема 1, т.к. не решает вопрос об экстремуме для случая, когда  не существует в точке C, а также
не существует в точке C, а также  .
.
Пример

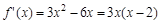
 - точки возможного экстремума
- точки возможного экстремума

3) Третье достаточное условие экстремума и перегиба.
Теорема 3.
Пусть
- n ³ 1 – целое число
- функция 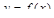 имеет производную порядка n в некоторой окрестности точки с и производную порядка n + 1 в самой точке С
имеет производную порядка n в некоторой окрестности точки с и производную порядка n + 1 в самой точке С
- справедливы следующие соотношения:

Тогда, если n является четным числом, график функции 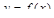 имеет перегиб в точке M(c, f(c)). Если же n является нечетным числом и, кроме того,
имеет перегиб в точке M(c, f(c)). Если же n является нечетным числом и, кроме того,  , функция
, функция 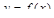 имеет локальный экстремум в точке с, точнее, локальный минимум при
имеет локальный экстремум в точке с, точнее, локальный минимум при  и локальный максимум при
и локальный максимум при  .
.
Доказательство (для случая экстремума)
Пусть n ³ 1 является нечетным числом и  . Т. к. при n = 1 теорема совпадает с Теоремой 2, то достаточно провести доказательство для нечетного n ³ 3. Для определенности проведем рассуждения для случая
. Т. к. при n = 1 теорема совпадает с Теоремой 2, то достаточно провести доказательство для нечетного n ³ 3. Для определенности проведем рассуждения для случая  . Для случая
. Для случая  они проводятся аналогично.
они проводятся аналогично.
Из условия  и из Теоремы
и из Теоремы
(Теорема: Если функция f (x) дифференцируема в точке с и  , то эта функция возрастает (убывает) в точке С), примененной к
, то эта функция возрастает (убывает) в точке С), примененной к  вытекает, что эта функция возрастает в точке С. Кроме того,
вытекает, что эта функция возрастает в точке С. Кроме того,  , то это означает, что найдется достаточно малая окрестность точки с, в пределах которой
, то это означает, что найдется достаточно малая окрестность точки с, в пределах которой  отрицательна слева от С и положительна справа от С. Разложим f’ (x) в окрестности точки С в ряд Тейлора с остаточным членом в форме Лагранжа. Мы получим, что для всех x из достаточно малой окрестности точки С между С и X найдется точка x такая, что
отрицательна слева от С и положительна справа от С. Разложим f’ (x) в окрестности точки С в ряд Тейлора с остаточным членом в форме Лагранжа. Мы получим, что для всех x из достаточно малой окрестности точки С между С и X найдется точка x такая, что

Соотношения  и условие
и условие  позволяют переписать это в виде
позволяют переписать это в виде

Т. к. x всегда лежит между C и X, то для всех X из достаточно малой окрестности точки C производная  отрицательна при
отрицательна при  и положительна при
и положительна при  . При нечетном n число n – 1 является четным, а поэтому вся правая (а, следовательно, и левая) часть
. При нечетном n число n – 1 является четным, а поэтому вся правая (а, следовательно, и левая) часть 
для всех X из достаточно малой окрестности C отрицательна слева от C и положительна справа от C.
На основании Теоремы 1 это означает, что функция f (x) имеет локальный минимум в точке C.
Случай  рассматривается совершенно аналогично.
рассматривается совершенно аналогично.