Рекомендуется применять разные методы обучения при решении задач по каждой теме. Сначала преподаватель у доски решает одну задачу, излагая методику и объясняя особенности; затем одну задачу решает у доски студент с помощью преподавателя (в форме диалога и обсуждения); следующие задачи студенты решают, помогая друг другу, на рабочих местах под контролем преподавателя с индивидуальными консультациями и с последующей записью решения на доске.
Прием расчетно-графической работы.
Прием расчетно-графической работы осуществляется в два этапа. На первом этапе проверяется правильность выполнения заданий по мере выполнения их студентами. Если выполненная работа удовлетворяет предъявляемым требованиям по содержанию и оформлению, начинается второй этап – собеседование. Во время собеседования студент, отвечая на поставленные вопросы, демонстрирует свои знания-умения по затронутым в работе темам. При оценке работы учитываются качество оформления расчетов и рисунков, уровень знаний, продемонстрированный в ответах на вопросы, самостоятельность и соблюдение сроков выполнения работы. По итогам собеседования студент допускается к зачету по дисциплине.
Методические рекомендации для обучающихся
Работа с конспектом.
Перед очередным занятием необходимо просмотреть рекомендованный преподавателем теоретический материал. Перед контрольной работой необходимо повторить весь теоретический и практический материал, в частности, решить типовой вариант контрольной работы.
Выполнение расчетно-графической работы.
Расчетно-графическая работа выполняется по типовой методике и выполняется в установленном временном режиме. Каждый студент группы выполняет свой вариант. В работу с учётом подготовленности студента могут быть включены элементы исследования с использованием средств компьютерной математики.
Подготовка к экзамену
Если студент добросовестно работал в семестре, то при подготовке к зачету ему остается только повторить изученный материал. В противном случае студенту предстоит нелегкая и малоэффективная зубрежка перед экзаменом.
Аннотация рабочей программы дисциплины
Б2.02 Математический анализ
Код и название направления подготовки (специальности):
231000 "Программная инженерия"
Квалификация (степень) выпускника: бакалавр
Форма обучения: очная
1. Цель дисциплины:
Формирование комплекса устойчивых знаний, умений и навыков, определяющих математическую подготовку бакалавров, необходимых и достаточных для осуществления всех видов профессиональной деятельности, предусмотренной образовательным стандартом.
2. Место дисциплины в структуре ООП:
Дисциплина относится к базовой части естественнонаучного цикла
3. Требования к результатам освоения дисциплины:
Процесс изучения дисциплины направлен на формирование и развитие компетенций (коды, в соответствии с ФГОС ВПО) ОК-6, ОК-10, ПК-12.
4. Общая трудоемкость дисциплины составляет 10 зачетных единиц (360 часов).
5. Основные разделы дисциплины: Пределы и непрерывные функции, производная и дифференциал, приложения к исследованию функций, интеграл, дифференциальное исчисление для функций нескольких переменных, кратные, криволинейные и поверхностные интегралы, дифференциальные уравнения, ряды.
6. Авторы: Салихов Владислав Хасанович, доцент, д.ф.-м.н..
7. Рабочая программа дисциплины рассмотрена на заседании кафедры от 03.09.2013г., протокол №1 и утверждена первым проректором по учебной работе «____»____________2014г.
Лекции i семестр
ЛЕКЦИЯ 1:
ВВЕДЕНИЕ В ДИСЦИПЛИНУ. ОСНОВНЫЕ ЭТАПЫРАЗВИТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА.
План лекции
1. Основные этапы развития математического анализа.
2. Роль математического анализа в математике, физике, информатике и других областях естествознания.
3. Элементарные функции.
4. Понятие предела функции.
5. Основные свойства пределов
· Введение
Математический анализ - фундаментальный раздел математики, что ведет свой отсчет от XVII века, когда было строго сформулировано теорию бесконечно малых. Современный математический анализ включает в себя также теорию функций, теории границ и рядов, дифференциальное и интегральное исчисление, дифференциальные уравнения и дифференциальную геометрию. Математический анализ возник выдающейся вехой в истории науки и сформировал лицо современной математики. Анализ быстро превратился в мощнейший инструмент для исследователей естественных наук, а также стал одним из двигателей научно-технической революции.
Следующим витком в развитии математического анализа стал сформированный в начале XX века функциональный анализ. Если классический анализ считает переменную числом - т.е. элементом из множества действительных (или комплексных) чисел, то в функциональном анализе уже сама функция рассматривается как переменная. Одновременно вводится понятие функционала - обобщенной функции, которые может принимать другую функцию в качестве аргумента (функция от функции). В современной формулировке, функциональный анализ является применением теории анализа к произвольному пространства математических объектов, в котором возможно определить понятие близости (топологическое пространство), или расстояния (метрическое пространство) между объектами.
· История возникновения
В истории математики можно условно выделить два основных периода: элементарной и современной математики. Границей, от которой ведется отсчет эпохи новой (иногда - высшего) математики, стало XVII века. Именно в XVII веке появился математический анализ. Предтечами был исчисления бесконечно малых в работах Валлиса, Грегори, Барроу. К концу XVII века Исааком Ньютоном, Готфридом Лейбницем был создан аппарат дифференциального и интегрального исчисления, что составляет основу математического анализа и даже математическую основу всего современного естествознания.
Движение, переменные величины и их взаимосвязь окружают нас повсюду. Различные виды движения, их закономерности составляют основной объект изучения конкретных наук физики, геологии, биологии, социологии и т.д. Точный язык и соответствующие математические методы описания и изучения таких величин оказались необходимыми во всех областях знаний примерно как числа и арифметика необходимы для описания количественных соотношений. Поэтому математический анализ стал основой языка и математических методов описания переменных и связей между ними. В наши дни без математического анализа невозможно было бы не только рассчитать космические траектории, работу ядерных реакторов, закономерности развития циклона, но и эффективно управлять производством, распределением ресурсов, организацией технологических процессов, ибо все это - динамичные процессы.
Элементарная математика была преимущественно математикой постоянных величин, она изучала главным образом соотношение между элементами геометрических фигур, арифметические свойства чисел и алгебраические уравнения.
· Предпосылки появления математического анализа
К концу XVII в. сложилась ситуация, когда в математике были накоплены знания о развязке некоторых важных классов задач (например, задачи о вычислении площадей и объемов нестандартных фигур, задача проведения касательных к кривым), а также появились методы решения различных частных случаев. Оказалось, что эти задачи тесно связаны с задачами описания некоторого (не обязательно равномерного) механического движения, и в частности вычисления его мгновенных характеристик (скорости, ускорение в любой момент времени), а также нахождение пройденного пути при движении, что происходит с заданной переменной скоростью. Решение этих задач было необходимо для дальнейшего развития физики, астрономии, техники. К середине XVII в. в работах Рене Декарта и Пьера Ферма были заложены основы аналитического метода координат (так называемой аналитической геометрии), которые позволили сформулировать различные по своему происхождению геометрические и физические задачи общим языком чисел и числовых зависимостей (числовых функций).
Все эти обстоятельства привели к тому, что в конце XVII столетия двум ученым Исааку Ньютону и Готфриду Лейбницу, независимо друг от друга, удалось создать математический аппарат для решения указанных задач. В своих трудах эти ученые собрали и обобщили некоторые результаты предшественников начиная от Архимеда и заканчивая своими современниками, такими как Бонавентура Кавальери, Блез Паскаль, Джеймс Грегори, Исаак Барроу. Этот аппарат и составил основу математического анализа - нового раздела математики, изучающего различные динамические процессы, т.е. взаимосвязи переменных, которые математики называют функциональными зависимостями или функциями.
· Вехи развития математического анализа
Понятие функции ввел в XVIII веке Леонард Эйлер. На протяжении XVIII века были развиты различные методы анализа, которые обогатили дифференциальное и интегральное исчисления: вариационное исчисление, теория рядов, теория обыкновенных дифференциальных уравнений.
Анализ функций действительной переменной начал набирать признаков отдельного раздела математики, когда Бернард Больцано дал современное определение непрерывности в 1816, хотя работы Больцано не получили широкую известность в 1870-х. С 1821 Огюстен Коши начал формировать прочное логическое основание под математическим анализом, формулируя его через понятие бесконечно малых. Ему также принадлежат понятия фундаментальной последовательности и основы анализа комплексной переменной. Симеон Пуассона, Джозеф Лиувилль, Джозеф Фурье и другие изучали дифференциальные уравнения и гармонический анализ. Благодаря вкладу этих и других математиков, таких как Карл Вейерштрасс развился епсилонний подход, который является основой современного математического анализа. Образцом такого подхода является определение предела через  и
и  .
.
Внутри XIX века Бернхард Риман развил теорию интегрирования. В дальнейшем математиков стало смущать то, что они предполагают существование континуума действительных чисел без доказательства. Решая эту проблему, Рихард Дедекинд сконструировал определения иррационального числа как сечение Дедекинда, таким образом, заполнив "пробелы" в рациональных числах и образовав полный метрическое пространство: континуум действительных чисел. Примерно тогда же попытки уточнить теоремы интегрирования по Риману привели к изучению разрывов действительных функций.
Стали возникать математические чудовища, такие как нигде непрерывная функция Дирихле, непрерывная, но нигде не дифференцированная функция Вейерштрасса, кривые, полностью заполняют плоскость вроде кривой Пеано. Решая проблемы с такими функциями, Камиль Жордан построил теорию меры Жордана, а Георг Кантор развил интуитивную теорию множеств. В начале ХХ века математический анализ был формализован теорией множеств. Анри Лебег решил проблему меры, а Давид Гильберт ввел Гильбертово пространство. Возникла идея нормированного векторного пространства, и в 1920-х Стефан Банах начал функциональный анализ.
2. Преподавание математического анализа в высшей школе
Математический анализ входит в общий курс высшей математики в большинстве технических вузов наряду с другими разделами математики, такими как аналитическая геометрия, теория дифференциальных уравнений, теория вероятностей и др. Для специальностей, требующих повышенного умения пользоваться математическим аппаратом, например для физиков, математический анализ излагается отдельным курсом.
Объем материала включает:
· понятие о числовую последовательность и ее свойства, сходимость, границу числовой последовательности;
· теорию функций действительного переменного, включая:
- понятие о границе функции, непрерывность;
- понятие о производной и дифференциал;
- понятие об особых точках (нули, экстремумы) и асимптоты функций;
- понятие первообразной;
- понятие интеграла, включающего основы теории степени;
- понятие об аппроксимации, интерполяцию и экстраполяцию.
- знакомство с некоторыми специальными функциями.
· теорию функций многих переменных, включающий:
- понятия частичной производной;
- понятие многомерного интеграла, поверхностного интеграла и линейного интеграла;
- основы векторного исчисления, понятия векторного поля, дивергенции и ротора;
- понятие о проблеме оптимизации.
· теорию рядов, включающий:
- понятие о числовом ряде и критерии его сходимости;
- понятие о степенном ряде и ряде Тейлора;
- понятие о ряде Фурье и попутно о преобразовании Фурье.
· основы численного анализа
Изучение математического анализа закладывает основы для подального изучения смежных дисциплин математики: комплексного анализа, дифференциальной геометрии, теории обыкновенных дифференциальных уравнений и дифференциальных уравнений с частными производными, подводящий к изучению задач математической физики и функционального анализа.
Предел – это такая величина, к которой стремится рассмотренная функция при стремлении ее аргумента к данной точке.
δ 

· 












Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).
Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.
Итак,  если
если  такое, что
такое, что


 δ
δ
· 


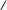




 x
x
 a
a 
Выполняется неравенство: 
Свойства пределов:
· 
- предел числа есть само число
·  *док-во
*док-во
- предел суммы равен сумме пределов
· 
- предел произведения равен произведению пределов
· 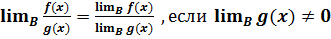
- предел частного равен частному пределов
Базы пределов:
B:
1) 






2) 

 x
x
a
3) 







 x
x
a
4) 






 x
x
c
5) 






 x
x
c
6) 








 x
x
-c c
* Доказательство  :
:
Пусть  ;
;

Для любого 

Из определения предела  найдем
найдем  такое, что
такое, что













 x
x 












 x
x 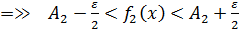
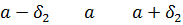
 выполняются оба неравенства (1) и (2):
выполняются оба неравенства (1) и (2):
 ,
,
т.е. 

Контрольные вопросы:
1. Что такое предел?
2. Какие существуют свойства предела?
3. Пояснить, что означает следующее утверждение:
4. Доказать теорему об арифметических операциях над функциями, имеющими предел.
ЛЕКЦИЯ 2: