План лекции
1. Дифференцирование параметрически заданных функций.
2. Неявные функции и их дифференцирование.
o Дифференцирование параметрически заданных функций
Пусть функция 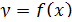 задана параметрическими уравнениями
задана параметрическими уравнениями
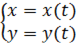 ;
;
где t – параметр.
Тогда производная этой функции по переменной 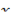 равна отношению производных
равна отношению производных  и
и 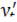 по параметру t:
по параметру t:
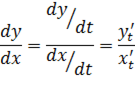
- Пример 1.
Найти производную функции  , заданной уравнениями в параметрической форме:
, заданной уравнениями в параметрической форме:
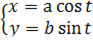 ;
;
Решение:
Очевидно, что 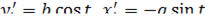 .
.
Следовательно,

- Пример 2.
Найти производную функции, заданной параметрически
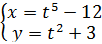
Решение:
Находим 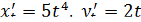 .
.
Следовательно:

o Неявные функции и их дифференцирование
Неявные функции - функции, заданные соотношениями между независимыми переменными, не разрешенными относительно последних; эти соотношения являются одним из способов задания функции. Например, соотношение

задаёт неявную функцию.
Если дифференцируемая в точке 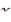 функция
функция 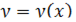 задана соотношением
задана соотношением  и если при этом функция
и если при этом функция 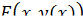 - дифференцируема в точке
- дифференцируема в точке  , то производную
, то производную 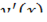 можно определить из равенства
можно определить из равенства
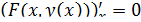 ,
,
так как функция  тождественно равна постоянной и, следовательно, ее производная равна нулю.
тождественно равна постоянной и, следовательно, ее производная равна нулю.
- Пример 1.
Продифференцировать выражение  по
по 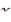 , считая
, считая 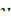 функцией от
функцией от  .
.
Решение:
Так как 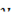 – это функция от
– это функция от 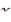 , то
, то 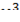 - это сложная функция. Ее можно условно представить как
- это сложная функция. Ее можно условно представить как  где
где 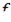 – функция возведения в куб, а
– функция возведения в куб, а 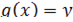 . Тогда, по формуле производной сложной функции имеем:
. Тогда, по формуле производной сложной функции имеем:

При дифференцировании второго выражения выносим константу за знак производной и действуем как в предыдущем случае (здесь  – функция синуса,
– функция синуса, 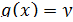 ):
):

Для третьего выражения применяем формулу производной произведения:
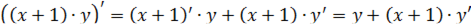
- Пример 2
Вычислите производную 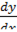 , если дифференцируемая функция задана неявно равенством
, если дифференцируемая функция задана неявно равенством
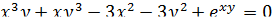
Решение:
Согласно теореме производную 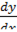 следует определять из равенства
следует определять из равенства 
Вычислим все производные в левой части этого соотношения, используя правила дифференцирования.
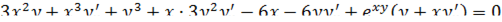 .
.
Из полученного равенства определим производную:
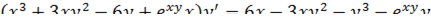
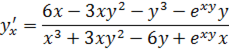
Контрольные вопросы:
1. Как найти производную параметрически заданной функции? Приведите пример.
2. Дайте определение неявной функции.
3. Как продифференцировать неявную функцию?
ЛЕКЦИЯ 11:
Механический смысл производной.
План лекции
1. Механический смысл производной.
2. Кривизна плоской кривой.
o Механический смысл производной
Напомним, как определялась скорость движения в курсе физики. Рассмотрим самый простой случай: материальная точка движется по координатной прямой, причем задан закон движения, т. е. координата  этой точки есть известная функция
этой точки есть известная функция  времени
времени  . За промежуток времени от
. За промежуток времени от  до
до 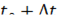 перемещение точки равно
перемещение точки равно 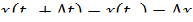 , а ее средняя скорость такова:
, а ее средняя скорость такова:
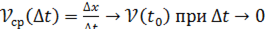 (1)
(1)
При 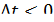 формула также верна: перемещение равно
формула также верна: перемещение равно  , а продолжительность промежутка времени равна
, а продолжительность промежутка времени равна  .
.
Обычно характер движения бывает таким, что при малых  средняя скорость практически не меняется, т. е. движение с большой степенью точности можно считать равномерным. Другими словами, значение средней скорости при
средняя скорость практически не меняется, т. е. движение с большой степенью точности можно считать равномерным. Другими словами, значение средней скорости при 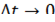 стремится к некоторому вполне определенному значению, которое и называют мгновенной скоростью
стремится к некоторому вполне определенному значению, которое и называют мгновенной скоростью  материальной точки в момент времени
материальной точки в момент времени  . Итак,
. Итак,
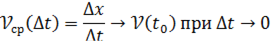
Но по определению производной
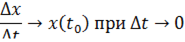
Поэтому считают, что мгновенная скорость 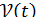 определена только для любой дифференцируемой функции
определена только для любой дифференцируемой функции 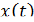 , при этом
, при этом
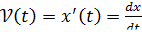 (2)
(2)
Коротко говорят: производная от координаты по времени есть скорость. В этом состоит механический смысл производной.
Мгновенная скорость может принимать как положительные, так и отрицательные значения, и, конечно, значение 0. Если скорость на каком-либо промежутке времени  положительна, то точка движется в положительном направлении, т. е. координата растет с течением времени, а если
положительна, то точка движется в положительном направлении, т. е. координата растет с течением времени, а если  отрицательна, то координата
отрицательна, то координата 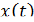 убывает.
убывает.
Аналогичное положение и с ускорением движения. Скорость движения точки есть функция от времени 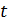 . А производная этой функции называется ускорением движения:
. А производная этой функции называется ускорением движения:
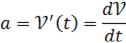
Коротко говорят: производная от скорости по времени есть ускорение.
o Движение по кривой













 B
B





 A
A

Теорема:
Если  или
или  – вектор скорости направлен по касательной и траектории движения, то
– вектор скорости направлен по касательной и траектории движения, то  или
или 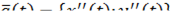 .
.
Доказательство:
Рассмотрим две точки при  и
и 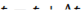 на траектории движения
на траектории движения 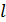 :
:
Заменим кривую на хорду, т.к.  очень мала.
очень мала.


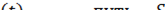
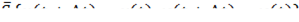

Вектором с предельными координатами называется предел вектора.

Вывод:
Вектор 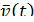 направлен по касательной, т.к. касательная – предельное положение секущей.
направлен по касательной, т.к. касательная – предельное положение секущей.
o Кривизна в точке
Кривизной в точке  называют предел отношения угла между векторами скорости и длины кривой.
называют предел отношения угла между векторами скорости и длины кривой.


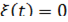




максимальное 
 Пример: равномерное движение по окружности.
Пример: равномерное движение по окружности.

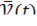
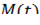

где 
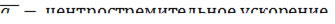
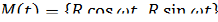
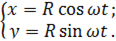
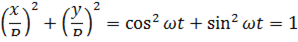
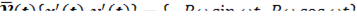
скалярное произведение
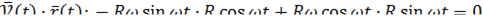


Контрольные вопросы:
1. Каков механический смысл производной?
2. Что такое предел вектора?
3. Дать определение касательной.
4. Что такое кривизна в точке? Привести пример.
ЛЕКЦИЯ 12-13