План лекции
1. Интегрирование тригонометрических функций.
При интегрировании тригонометрических функций используются приемы, позволяющие понижать степени, избавляться от произведения и т.д., т.е. необходимо использовать тригонометрические формулы.
- Интегралы вида 
Для решения данных интегралов применяются формулы преобразования произведения тригонометрические функций в сумму или разность:
- Интегралы вида 
Здесь и везде ниже предполагается, что 
и 
- натуральные числа. Для вычисления таких интегралов используются следующие подстановки и преобразования:
o Если степень косинуса - нечетная (при этом степень синуса может быть любой), то используется подстановка 
.
o Если степень синуса - нечетная, то используется подстановка 
.
o Если степени и - четные, то сначала применяются формулы двойного угла:
чтобы понизить синус или косинус в подынтегральном выражении. Затем, если необходимо, применяются вышеуказанные правила.
- Интегралы вида 
Степень подынтегрального выражения в данном интеграле можно понизить с помощью тригонометрического соотношения 
и формулы редукции:
- Интегралы вида 
Здесь степень подынтегрального выражения понижается с помощью соотношения 
и формулы редукции:
Примеры:
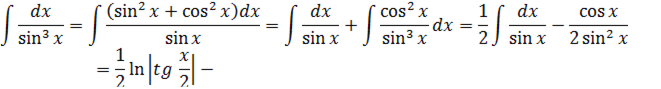
Контрольные вопросы:
1. Как происходит интегрирование тригонометрических функций?
2. Какие виды интегрирования тригонометрических функций приводятся в данной лекции?
ЛЕКЦИЯ 16:
ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
План лекции
1. Интегрирование иррациональных функций.
2. Понятие о специальных функциях.
o Интегрирование иррациональных функций
Класс иррациональных функций очень широк, поэтому универсального способа их интегрирования просто быть не может. Попытаемся выделить наиболее характерные виды иррациональных подынтегральных функций и поставить им в соответствие метод интегрирования.
· Используя метод непосредственного интегрирования, достаточно просто находятся неопределенные интегралы вида 
, где 
– рациональная дробь, 
и 
– действительные коэффициенты.
Пример:
Найти множество первообразных функции
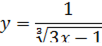
Решение:
Правило интегрирования 
и таблица первообразных сразу приводят нас к ответу:
· Бывают случаи, когда уместно использование метода подведения под знак дифференциала. Например, при нахождении неопределенных интегралов вида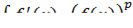 
, где 
– рациональная дробь.
Пример:
Найти неопределенный интеграл
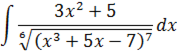
Решение:
Не трудно заметить, что 
. Следовательно, подводим под знак дифференциала и используем таблицу первообразных:
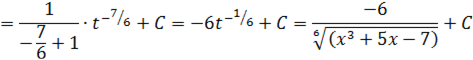
· Достаточно часто приходится иметь дело с неопределенными интегралами вида
где 
и 
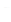– действительные коэффициенты.
В этом случае выделяем полный квадрат под знаком корня:
и используем формулу из таблицы неопределенных интегралов
То есть,
Пример:
Найти неопределенный интеграл
Решение:
В подкоренном выражении выделяем полный квадрат:
Поэтому
· Аналогично проводится интегрирование иррациональных функций вида
Пример:
Найдите неопределенный интеграл
Решение:
Выделим полный квадрат в выражении под знаком корня:
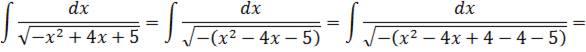
Пришли к табличному интегралу 
, поэтому
· Нахождение множества первообразных иррациональных функций
где 
, 
, 
и – действительные коэффициенты, очень схоже с интегрированием простейших дробей третьего типа: выполняется подведение под знак дифференциала, затем выделяется полный квадрат подкоренного выражения и применяются формулы из таблицы первообразных.
Пример:
Найти множество первообразных функции
Решение:
Так как 
, то
Поэтому
· Неопределенные интегралы иррациональных функций вида
находятся методом подстановки.
В зависимости от рациональных чисел 
вводят следующие новые переменные:
1. Если - целое число, то принимают 
, где 
- общий знаменатель чисел и .
2. Если 
- целое число, то 
, где - знаменатель числа .
3. Если 
- целое число, то вводят новую переменную 
, где 
- знаменатель числа .
Пример:
Найти неопределенный интеграл
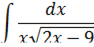
Решение:
То есть, 
, 
. Так как 
- целое число, то вводим новую переменную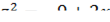 
(
– знаменатель числа ).
Выражаем через 
:
Выполняем подстановку в исходный интеграл:
o Понятие о специальных функциях
Сначала дадим несколько определений, чтобы дальнейшее понятие было рассмотрено более понятно.
Трансцендентное уравнение — уравнение, не являющееся алгебраическим. Обычно это уравнения, содержащие показательные, логарифмические, тригонометрические, обратные тригонометрические функции, например:
Дифференциальное уравнение — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке.
Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения вида
Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).
А теперь приступим к самому понятию специальных функций.
Специальные функции — встречающиеся в различных приложениях математики (чаще всего — в различных задачах математической физики) функции, которые не выражаются через элементарные функции. Специальные функции представляются в виде рядов или интегралов.
Специальные функции возникают обычно из следующих соображений:
- «неберущиеся» интегралы:
- решения трансцендентных уравнений, не выражающиеся в элементарных функциях;
- решения дифференциальных уравнений, не выражающиеся в элементарных функциях;
- ряды, не сходящиеся к элементарным функциям;
- математическое выражение свойств чисел;
- необходимость задания функции с необычными свойствами.
Это разделение не является строгим, поскольку, например, большинство неэлементарных решений дифференциальных уравнений удалось выразить через неберущийся интеграл или в виде ряда. Поэтому не существует строгой классификации трансцендентных функций
Большинство специальных функций являются трансцендентными.
· Функции-интегралы
К таким специальным функциям относятся: бета-функция, гамма-функция, интегральный логарифм, интеграл вероятности, интегральный синус, интегральный косинус, эллиптические функции.
· Функции-ряды
К таким функциям относятся гипергеометрическая функция, дзета-функция.
· Неэлементарные решения дифференциальных уравнений
К таким специальным функциям относятся: сферические функции, цилиндрические функции, функции Эйри, функции параболического цилиндра, функции Матьё.
· Необычные функции
Существует много функций с необычным поведением, придуманных для различных целей. Это функция Дирихле, функция Хэвисайда.
· Функции, выражающие свойства чисел
Эти функции обычно связаны с простейшими свойствами чисел. Сюда, прежде всего, можно отнести специальные арифметические функции, модуль, знак числа, факториал.
Контрольные вопросы:
1. Какие методы интегрирования иррациональных функций приведены в лекции?
2. Какие виды иррациональных функций интегрируются в данной лекции?
3. Что такое трансцендентное уравнение?
4. Что такое дифференциальное уравнение?
5. Понятие о числовом ряде.
6. Что такое специальная функция?
ЛЕКЦИЯ 17: