Примеры:
1. Рассмотрим функцию  .
.
Её производная существует при всех  и равна
и равна  . Следовательно, все критические точки - стационарные и задаются уравнением
. Следовательно, все критические точки - стационарные и задаются уравнением  . Это уравнение можно записать в виде
. Это уравнение можно записать в виде  ; оно имеет единственный корень
; оно имеет единственный корень  : это единственная стационарная точка. Записав функцию в виде
: это единственная стационарная точка. Записав функцию в виде  , легко увидеть, что в стационарной точке
, легко увидеть, что в стационарной точке  функция имеет минимум, равный
функция имеет минимум, равный  .
.

2. Найти экстремумы функции  .
.
Решение

Так как  , то критические точки функции
, то критические точки функции  и
и  . Экстремумы могут быть только в этих точках. Так как при переходе через точку
. Экстремумы могут быть только в этих точках. Так как при переходе через точку  производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку
производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку  производная меняет знак минус на плюс, поэтому в точке
производная меняет знак минус на плюс, поэтому в точке  у функции минимум. Вычислив значения функции в точках
у функции минимум. Вычислив значения функции в точках
 и
и 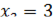 , найдем экстремумы функции: максимум
, найдем экстремумы функции: максимум  и минимум
и минимум  .
.
Контрольные вопросы:
1. Сформулировать теорему Ролля. В чем ее геометрический смысл? Каково следствие из теоремы?
2. Сформулировать теорему Лагранжа о среднем значении. Каково ее геометрическое и механическое истолкования?
3. Сформулировать теорему Коши о среднем значении. В чем ее геометрический смысл?
4. Что такое возрастающая / убывающая функция? Назовите примеры таких функций.
5. Что такое экстремум функции? Назовите три достаточных условий экстремума.
ЛЕКЦИЯ 7:
ПРАВИЛО ЛОПИТАЛЯ РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТЕЙ
План лекции
1. Правило Лопиталя раскрытия неопределенностей.
2. Формула Тейлора.
3. Применение формулы Тейлора для приближенного вычисления значений основных элементарных функций.
o Правило Лопиталя
метод нахождения пределов функций, раскрывающий неопределённости вида  и
и  . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
1) Точная формулировка
Условия:
1. 
2. 
3. 
4. 
Пределы также могут быть односторонними.
2) Доказательство
- Отношение бесконечно малых
Докажем теорему для случая, когда пределы функций равны нулю (то есть неопределённость вида 
Поскольку мы рассматриваем функции  и
и  только в правой проколотой полуокрестности точки
только в правой проколотой полуокрестности точки  , мы можем непрерывным образом их доопределить в этой точке: пусть
, мы можем непрерывным образом их доопределить в этой точке: пусть 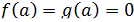 . Возьмём некоторый
. Возьмём некоторый 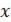 из рассматриваемой полуокрестности и применим к отрезку
из рассматриваемой полуокрестности и применим к отрезку  теорему Коши. По этой теореме получим:
теорему Коши. По этой теореме получим:  ,
,

Дальше, записав определение предела отношения производных и обозначив последний через  , из полученного равенства выводим:
, из полученного равенства выводим:


что является определением предела отношения функций.
- Отношение бесконечно больших
Докажем теорему для неопределённостей вида  .
.
Пусть, для начала, предел отношения производных конечен и равен  . Тогда, при стремлении
. Тогда, при стремлении 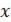 к
к  справа, это отношение можно записать как
справа, это отношение можно записать как  , где
, где 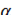 — O (большое). Запишем это условие:
— O (большое). Запишем это условие:
 .
.
Зафиксируем  из отрезка
из отрезка  и применим теорему Коши ко всем
и применим теорему Коши ко всем  из отрезка
из отрезка  :
:
 , что можно привести к следующему виду:
, что можно привести к следующему виду:
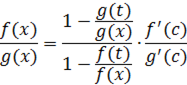
Для  , достаточно близких к
, достаточно близких к  , выражение имеет смысл. Предел первого множителя правой части равен единице (так как
, выражение имеет смысл. Предел первого множителя правой части равен единице (так как  и
и 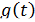 — константы, а
— константы, а  и
и  стремятся к бесконечности). Значит, этот множитель равен
стремятся к бесконечности). Значит, этот множитель равен  , где
, где 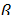 — бесконечно малая функция при стремлении
— бесконечно малая функция при стремлении 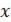 к
к  справа. Выпишем определение этого факта, используя то же значение
справа. Выпишем определение этого факта, используя то же значение  , что и в определении для α:
, что и в определении для α:
 .
.
Получили, что отношение функций представимо в виде  , и
, и
 . По любому данному
. По любому данному  можно найти такое
можно найти такое  , чтобы модуль разности отношения функций и
, чтобы модуль разности отношения функций и  был меньше
был меньше  , значит, предел отношения функций действительно равен
, значит, предел отношения функций действительно равен  .
.
Если же предел  бесконечен (допустим, он равен плюс бесконечности), то
бесконечен (допустим, он равен плюс бесконечности), то

В определении  будем брать
будем брать 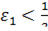 ; первый множитель правой части будет больше 1/2 при
; первый множитель правой части будет больше 1/2 при 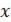 , достаточно близких к
, достаточно близких к  , а тогда
, а тогда 
Для других баз доказательства аналогичны приведённым.
3) Примеры


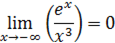



Первый «замечательный» предел:
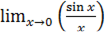 - пример неопределенности вида
- пример неопределенности вида 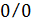 . По правилу Лопиталя:
. По правилу Лопиталя:

o Формула Тейлора
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема Тейлора:
Пусть функция  имеет в точке
имеет в точке  и некоторой ее окрестности производные порядка
и некоторой ее окрестности производные порядка  . Тогда между точками
. Тогда между точками  и
и  найдется такая точка
найдется такая точка  , что справедлива следующая формула,
, что справедлива следующая формула,

называемая формулой Тейлора, а выражение:

представляет остаточный член в форме Лагранжа
Доказательство**
Пусть

где, как указано в формулировке теоремы Тейлора,

Достаточно показать, что

Доказательство основано на повторяющемся применении правила Лопиталя. Заметим, что каждое  . Отсюда каждая следующая производная числителя функции
. Отсюда каждая следующая производная числителя функции  стремится к нулю в точке
стремится к нулю в точке  , и то же самое справедливо для знаменателя. Тогда
, и то же самое справедливо для знаменателя. Тогда
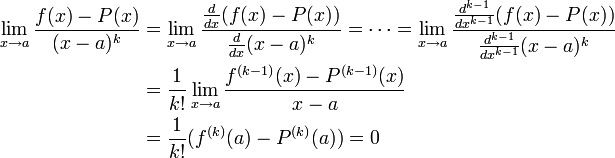
где переход от предпоследнего выражения к последнему следует из определения производной в точке  .
.
Ряды Тейлора для некоторых функций

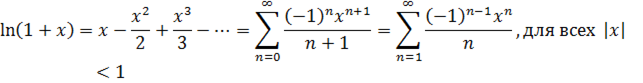


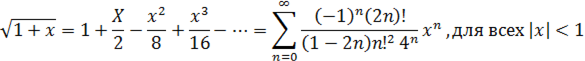



Контрольные вопросы:
1. Сформулируйте правило Лопиталя. Какого вида неопределенности необходимы для правила Лопиталя.
2. Где используется формула Тейлора?
3. Сформулируйте теорему Тейлора.
ЛЕКЦИЯ 8: