План лекции
1. Первообразная и неопределенный интеграл.
2. Свойство линейности.
3. Таблица неопределенных интегралов.
4. Замена переменной и интегрирование по частям.
o Первообразная и неопределенный интеграл.
- Определение первообразной.
Первообразной функции  на промежутке
на промежутке  называется такая функция
называется такая функция  , что выполняется равенство
, что выполняется равенство  для любого
для любого  из заданного промежутка.
из заданного промежутка.
Если принять во внимание тот факт, что производная от константы  равна нулю, то справедливо равенство
равна нулю, то справедливо равенство  . Так, например, функция
. Так, например, функция  является первообразной
является первообразной  . Так как производная константы равна нулю,
. Так как производная константы равна нулю, 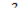 будет иметь бесконечное количество первообразных, таких как
будет иметь бесконечное количество первообразных, таких как 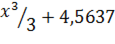 или
или 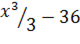 … и т. д. Таким образом, семейство первообразных функции
… и т. д. Таким образом, семейство первообразных функции  можно обозначить как
можно обозначить как 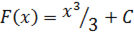 , где С – любое число.
, где С – любое число.
- Определение неопределенного интеграла.
Все множество первообразных функции  называется неопределенным интегралом этой функции и обозначается
называется неопределенным интегралом этой функции и обозначается  .
.
Выражение  называют подынтегральным выражением, а
называют подынтегральным выражением, а  – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции
– подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции  .
.
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция 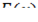 , а множество ее первообразных
, а множество ее первообразных  .
.
- Свойства первообразной
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
1. 
Производная результата интегрирования равна подынтегральной функции.
2. 
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.
3.  , где
, где 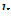 – произвольная константа.
– произвольная константа.
Коэффициент можно выносить за знак неопределенного интеграла.
4. 
Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.
Первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.
- Пример:
Найти первообразную функции 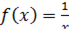 , значение которой равно единице при
, значение которой равно единице при  .
.
Решение:
Мы знаем из дифференциального исчисления, что  (достаточно заглянуть в таблицу производных основных элементарных функций). Таким образом,
(достаточно заглянуть в таблицу производных основных элементарных функций). Таким образом,
 . По второму свойству
. По второму свойству  . То есть, имеем множество первообразных
. То есть, имеем множество первообразных 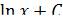 . При
. При  получим значение
получим значение  . По условию, это значение должно быть равно единице, следовательно, С = 1. Искомая первообразная примет вид
. По условию, это значение должно быть равно единице, следовательно, С = 1. Искомая первообразная примет вид  .
.
- Замена переменной
Суть метода заключается в том, что мы вводим новую переменную, выражаем подынтегральную функцию через эту переменную, в результате приходим к табличному (или более простому) виду интеграла.
Очень часто метод подстановки выручает при интегрировании тригонометрических функций и функций с радикалами.

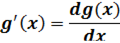
Примеры:



- Интегрирование по частям
Этот метод является очень мощным инструментом интегрирования.
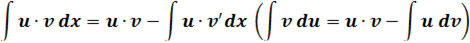
доказательство:


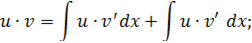

В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата.
Примеры:





o Таблица первообразных (неопределенных интегралов)
- рациональные функции:





- логарифмы





- экспоненциальные функции


- иррациональные функции


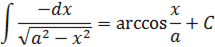




- тригонометрические функции



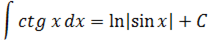



Вывод формул:




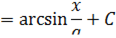








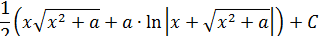
Контрольные вопросы:
1. Что такое первообразная функции? Назовите ее свойства.
2. Дать определение неопределенному интегралу.
3. В чем заключается суть интегрирования методом замены переменной? Приведите примеры.
4. Что такое метод интегрирования по частям? В чем его суть?
ЛЕКЦИЯ 14:
ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ.
План лекции
1. Интегрирование рациональных функций.
Функция 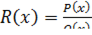 , где
, где  - многочлены от
- многочлены от  – называется рациональной.
– называется рациональной.
Если степень многочлена  меньше степени многочлена
меньше степени многочлена  , то
, то  называется правильной функцией.
называется правильной функцией.
Теорема:
Любую правильную рациональную функцию можно представить в виде суммы простейших правильных рациональных функций.
Для интегрирования рациональной функции, используется следующая последовательность шагов:
1. Если дробь неправильная (т.е. степень  больше степени
больше степени 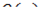 ), преобразовать ее в правильную, выделив целую часть – многочлен от
), преобразовать ее в правильную, выделив целую часть – многочлен от  .
.
Разделим многочлен  на
на  . Получим следующее выражение:
. Получим следующее выражение:
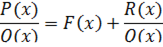
где  - неправильная рациональная дробь,
- неправильная рациональная дробь, 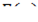 - целая часть,
- целая часть,  - дробная часть
- дробная часть
2. Разложить знаменатель  на произведение одночленов и/или несократимых квадратичных выражений.
на произведение одночленов и/или несократимых квадратичных выражений.
Запишем многочлен знаменателя  в виде:
в виде:
 ,
,
где квадратичные функции не имеют действительных корней.
3. Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов.
Запишем рациональную функцию в следующем виде:

Общее число неопределенных коэффициентов  должно быть равно степени знаменателя
должно быть равно степени знаменателя  .
.
Затем умножим обе части полученного уравнения на знаменатель  и приравняем коэффициенты при слагаемых с одинаковыми степенями
и приравняем коэффициенты при слагаемых с одинаковыми степенями  . В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов
. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов  Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов.
Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов.
4. Вычислить интегралы от простейших дробей.
Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул:


У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат:
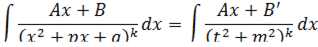
 . Затем применяются следующие формулы:
. Затем применяются следующие формулы:


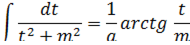
Интеграл  может быть вычислен за k шагов с помощью формулы редукции:
может быть вычислен за k шагов с помощью формулы редукции:

- Пример 1:
Вычислить интеграл

Решение:
Разложим подынтегральное выражение на простейшие дроби:

Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями:

Следовательно,

Тогда

Теперь легко вычислить исходный интеграл

- Пример 2:
Вычислить интеграл
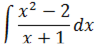
Решение:
Сначала выделим правильную рациональную дробь, разделив числитель на знаменатель.

Получаем

- Пример 3:
Вычислить интеграл
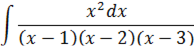
Решение:
Разложим подынтегральное выражение на сумму простейших дробей, используя метод неопределенных коэффициентов:

Приводя к общему знаменателю, получим:

Следовательно,

Получаем

Интеграл, соответственно, равен

Контрольные вопросы:
1. Какая функция называется рациональной?
2. Что такое правильная функция?
3. Каков алгоритм интегрирования правильной рациональной функции?
ЛЕКЦИЯ 15: