План лекции
1. Выпуклость и вогнутость функции, точки перегиба.
2. Асимптоты функции.
o Выпуклость и вогнутость функции, точки перегиба
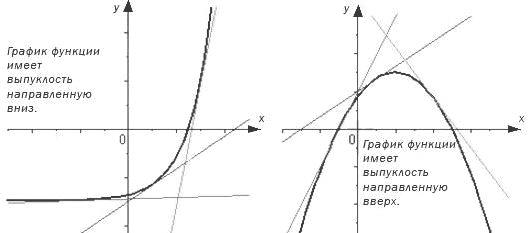
Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.
Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.
Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.
Посмотрите на чертеж, иллюстрирующий эти определения.
Точка  называется точкой перегиба графика функции
называется точкой перегиба графика функции  , если в данной точке существует касательная к графику функции (она может быть параллельна оси
, если в данной точке существует касательная к графику функции (она может быть параллельна оси  ) и существует такая окрестность точки
) и существует такая окрестность точки  , в пределах которой слева и справа от точки
, в пределах которой слева и справа от точки  график функции имеет разные направления выпуклости.
график функции имеет разные направления выпуклости.
Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.
На рисунке ниже представлены несколько примеров точек перегиба. Заметим, что некоторые функции могут не иметь точек перегиба, а другие могут иметь одну, несколько или бесконечно много точек перегиба.

Условия существования:
- Необходимое условие существования точки перегиба:
если функция 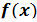 , дважды дифференцируемая в некоторой окрестности точки
, дважды дифференцируемая в некоторой окрестности точки 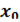 , имеет в
, имеет в 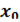 точку перегиба, то
точку перегиба, то 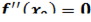 .
.
- Достаточное условие существования точки перегиба:
если функция  в некоторой окрестности точки
в некоторой окрестности точки 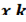 раз непрерывно дифференцируема, причем
раз непрерывно дифференцируема, причем 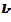 нечётно и
нечётно и 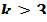 , и
, и 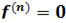 при
при  , а
, а  , то функция
, то функция  имеет в
имеет в 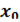 точку перегиба.
точку перегиба.
Пример:
Рассмотрим график функции 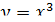 :
:

Эта функция является вогнутой при 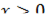 и выпуклой при
и выпуклой при 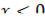 . В самом деле,
. В самом деле, 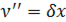 , но
, но 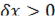 при
при 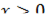 и
и  при
при  , следовательно,
, следовательно, 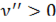 при
при 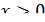 и
и 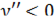 при
при 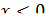 , откуда следует, что функция
, откуда следует, что функция  является вогнутой при
является вогнутой при 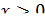 и выпуклой при
и выпуклой при 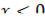 . Тогда
. Тогда 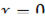 является точкой перегиба функции
является точкой перегиба функции  .
.
o Асимптоты функции (вертикальные, горизонтальные и наклонные)
Асимптота — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность.
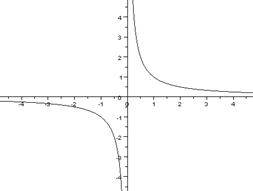
Для гиперболы  асимптотами являются оси абсцисс и ординат. Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее
асимптотами являются оси абсцисс и ординат. Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее
Виды асимптот графиков
- Вертикальная
Вертикальная асимптота — прямая вида 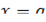 при условии существования предела
при условии существования предела 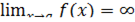 .
.
Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
1. 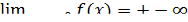 ;
;
2. 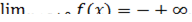
Замечание: обратите внимание на знаки бесконечностей в этих равенствах.
- Горизонтальная
Горизонтальная асимптота — прямая вида  при условии существования предела
при условии существования предела  .
.
- Наклонная
Наклонная асимптота — прямая вида  при условии существования пределов
при условии существования пределов 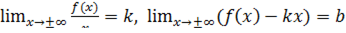
 Замечание:
Замечание:
функция может иметь не более двух наклонных (горизонтальных) асимптот.
Замечание:
если хотя бы один из двух упомянутых выше пределов не существует (или равен 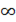 ), то наклонной асимптоты при
), то наклонной асимптоты при 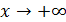 (или
(или 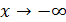 ) не существует.
) не существует.
Связь между наклонной и горизонтальной асимптотами
Если при вычислении предела 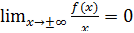 , то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?
, то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?
Дело в том, что горизонтальная асимптота является частным случаем наклонной при  , и из выше указанных замечаний следует, что
, и из выше указанных замечаний следует, что
1. Функция имеет или только одну наклонную асимптоту, или одну горизонтальную асимптоту, или одну наклонную и одну горизонтальную, или две наклонных, или две горизонтальных, либо же вовсе не имеет асимптот.
2. Существование указанных в п. 1. асимптот напрямую связано с существованием соответствующих пределов.
Порядок нахождения асимптот
1. Нахождение вертикальных асимптот.
2. Нахождение двух пределов 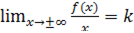
3. Нахождение двух пределов 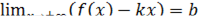 :
:
если  в п. 2., то
в п. 2., то  , и предел
, и предел 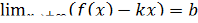 ищется по формуле горизонтальной асимптоты,
ищется по формуле горизонтальной асимптоты,  .
.
Наклонная асимптота — выделение целой части
Также наклонную асимптоту можно найти, выделив целую часть. Например:
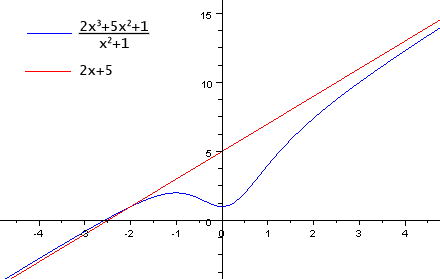
Дана функция 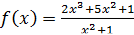 .
.
Разделив нацело числитель на знаменатель, получим:
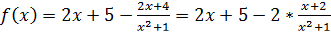 .
.
При 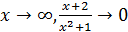 , то есть:
, то есть: 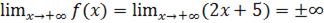 ,
,
и  является искомым уравнением асимптоты.
является искомым уравнением асимптоты.
Контрольные вопросы:
1. Что такое выпуклая / вогнутая функция?
2. Дайте определение точке перегиба функции.
3. Назовите достаточное и необходимое условия существования.
4. Что такое асимптота? Какие виды асимптот вы знаете?
ЛЕКЦИЯ 9: