План лекции
1. Дифференциальное исчисление функции одной переменной.
2. Правила дифференцирования.
3. Таблица производных.
Пусть дана  функция
функция 
Разность 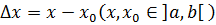 называется приращением аргумента в точке x 0.
называется приращением аргумента в точке x 0.
Разность  называется приращением значений функции
называется приращением значений функции  в точке x 0.
в точке x 0.
Если существует предел (конечный или бесконечный)
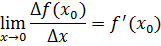
то он называется производной (конечной или бесконечной) функции f в точке x 0.
Свойства производной:
· 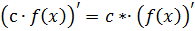
- константу можно вынести за знак производной;
· 
- производная суммы равна сумме производных;
· 
- производная произведения двух функций равна сумме двух слагаемых; первое слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции.

Производная частного равна разности произведений, в каждом из которых все функции сами по себе и одна производная, деленной на квадрат знаменателя
· 
производная сложной функции равна произведению производной внешней функции на производную от внутренней функции
Таблица производных:
1. 
2. 
3. 
4. 
5. 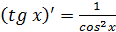
6. 
7. 
8. 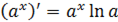
9. 
10. 
11. 
12. 
13. 
Вывод производных:
· При выводе самой первой формулы таблицы будем исходить из определения производной функции в точке. Возьмем  – любое действительное число, т.е.
– любое действительное число, т.е.  Запишем предел отношения приращения функции к приращению аргумента при
Запишем предел отношения приращения функции к приращению аргумента при 

· Формула производной степенной функции имеет вид  , где показатель степени n – любое действительное число. Докажем сначала формулу для натурального показателя степени, то есть, для n = 1, 2, 3, … Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:
, где показатель степени n – любое действительное число. Докажем сначала формулу для натурального показателя степени, то есть, для n = 1, 2, 3, … Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:

Для упрощения выражения в числителе обратимся к формуле бинома Ньютона:
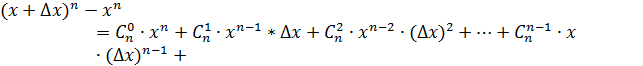


Следовательно:




Этим доказана формула производной степенной функции для натурального показателя.
· По определению производной для функции синуса имеем:

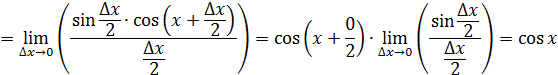


· Вывод формул таблицы производных для тангенса и котангенса проведем с использованием доказанных правил дифференцирования (производная дроби):

Производная котангенса находится аналогично.
· 


· Вывод формулы производной приведем на основе определения:

Пришли к неопределенности. Для ее раскрытия введем новую переменную  .
.
В последнем переходе мы использовали формулу перехода к новому основанию логарифма. Выполним подстановку в исходный предел:


Если вспомнить второй «замечательный» предел, то придем к формуле производной показательной функции:

· Докажем формулу производной логарифмической функции для всех  из области определения и всех допустимых значениях основания a логарифма. По определению производной имеем:
из области определения и всех допустимых значениях основания a логарифма. По определению производной имеем:



Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство  справедливо в силу второго замечательного предела.
справедливо в силу второго замечательного предела.
· 

Осталось провести преобразования. Так как областью значений арксинуса является интервал
 , то
, то 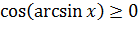 . Поэтому
. Поэтому 
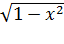 ,
, 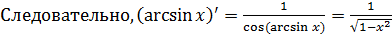


· Найдем производную арктангенса.
Для  обратной функцией является
обратной функцией является 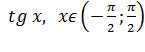

Выразим арктангенс через арккосинус, чтобы упростить полученное выражение.
Пусть  тогда
тогда
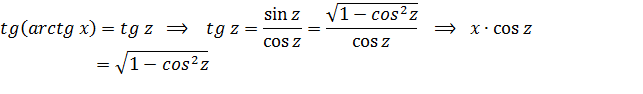


Следовательно,
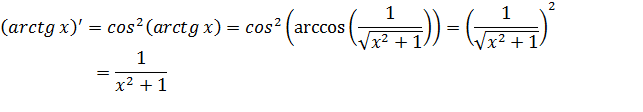
Схожим образом находится производная арккотангенса:

Несколько примеров нахождения производной:
· 
· 
· 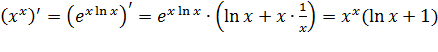
Контрольные вопросы:
1. Что называется приращением значений функции?
2. Что такое приращение аргумента в точке x 0?
3. Производная функции, ее свойства.
ЛЕКЦИЯ 5: