План лекции
1. Формула Ньютона — Лейбница
2. Геометрический смысл определенного интеграла.
3. Вычисление площадей, длин дуг, объемов тел вращения.
4. Вычисление объемов с помощью сечений.
o Формула Ньютона — Лейбница
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определённого интеграла и вычислением первообразной.
Если 
непрерывна на отрезке 
и 
— её любая первообразная на этом отрезке, то имеет место равенство:
Определенный интеграл от непрерывной функции равен разности значений первообразной функции (или неопределенного интеграла) при верхнем и нижнем пределах.
o Геометрический смысл определенного интеграла
Eсли 
непрерывна и положительна на [a, b], то интеграл
представляет собой площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми 
и 
и графиком функции .
Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функция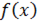 
, заданная на промежутке [a, b], равна нулю во всех точках этого промежутка, кроме конечного числа точек 
. Составим для 
интегральную сумму δ.
Пусть из точек 
, входящих в определение 
точек совпадают с точками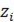 
, а остальные отличны от них. Тогда в сумме δ будет лишь 
слагаемых, отличных от нуля. Если наибольшее из чисел 
| есть 
, то, очевидно, 
,
откуда ясно, что при λ → 0 будет и δ → 0. Таким образом, интеграл
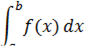
существует и равен нулю.
Приведем теперь пример функции, не имеющей интеграла. Пусть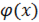 
задана на промежутке 
так:
Если мы, составляя сумму δ, за точки 
выберем числа иррациональные, то окажется δ = 0. Если же все 
взять рациональными, то получится δ = 1. Таким образом, за счет одного лишь уменьшения 
нельзя приблизить δ к какому-либо постоянному числу, и интеграл
Не существует.
В настоящее время известны точные признаки, позволяющие судить, имеет или нет заданная функция определенный интеграл, но мы ограничимся вышеприведенной теоремой об интегрируемости непрерывных функций.
o Вычисление площадей
Рассмотрим криволинейную трапецию, т.е. фигуру, образованную осью 
, прямыми 
, 
и кривой 
.
Требуется найти площадь данной криволинейной трапеции. Покажем, что эта задача эквивалентна нахождению определенного интеграла.
Разобьем отрезок 
на частей точками 
.
Получаем, что отрезок есть объединение полуинтервалов открытых слева 
, и отрезка 
, т.е.
(эти полуинтервалы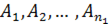 
и отрезок 
будем называть множествами).
Возьмем из каждого множества 
произвольную точку 
и составим следующую сумму:
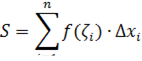
где 
длина (мера) множества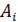 
(полуинтервала).
Величина 
это сумма площадей прямоугольников со сторонами 
и 
. При стремлении к нулю 
сумма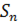 
будет стремиться к значению определенного интеграла
Получаем, что площадь криволинейной трапеции есть
Рассмотрим случай задания кривой параметрическим образом, т.е.
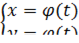
где параметр 
. Тогда площадь вычисляется через определенный интеграл:
Аналогично можно рассмотреть случай, когда криволинейная трапеция прилегает к оси , т.е. криволинейная трапеция ограничена линиями 
, 
, осью 
и кривой 
. В этом случае площадь вычисляется через интеграл:
o Вычисление длины дуги плоской кривой
Длиной дуги кривой линии называют предел, к которому стремится
длина вписанной в нее ломаной линии при неограниченном увеличении числа
ее звеньев и при стремлении длины наибольшего звена к нулю.
Пусть известна функция и требуется найти длину дуги, заданной функцией , где 
.
Для определения длины дуги 
необходимо вычислить определенный интеграл:
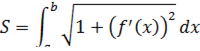
Рассмотрим случай параметрического задания кривой:
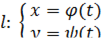
где 
. В этом случае для определения длина дуги вычисляется определенный интеграл:
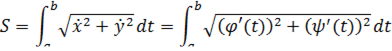
Рассмотрим случай, когда кривая задается в полярных координатах 
, где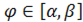 
. Тогда для определения длины дуги вычисляется следующий определенный интеграл:
o Вычисление объема тела вращения
Рассмотрим криволинейную трапецию, т.е. фигуру, образованную прямыми , 
, осью 
и функцией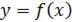 
.
Требуется найти объем тела вращения, образованного вращением криволинейной трапеции вокруг оси 
.
Объем данного тела вычисляется по формуле, содержащей определенный интеграл:
Если криволинейная трапеция прилегает к оси 
(прямые , 
, ось 
и функция ), тогда объем тела также определяется по формуле, содержащей интеграл:
o Вычисление площади поверхности вращения
Найдем площадь поверхности, которая образуется вращением кривой вокруг оси 
, где 
.
Указанную площадь можно получить вычислением определенного интеграла:
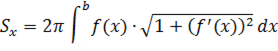
Теперь рассмотрим случай, когда вращаем кривую вокруг оси 
, где 
.
В этом случае площадь определяется вычислением следующего определенного интеграла:
Контрольные вопросы:
1. Сформулируйте теорему и назовите формулу Ньютона-Лейбница.
2. Каков геометрический смысл определенного интеграла?
3. Как вычислить площадь, длину дуги, объемы тел вращения с помощью определенного интеграла?
ЛЕКЦИЯ 19: