2. Если подынтегральной функции не существует в точке  :
:
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:

Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению  слева. По оси
слева. По оси  мы должны бесконечно близко приблизиться к точке разрыва слева.
мы должны бесконечно близко приблизиться к точке разрыва слева.
Пример
Вычислить несобственный интеграл и установить его расходимость.

Подынтегральная функция терпит бесконечный разрыв в точке  (устно проверяем, что с другим пределом интегрирования всё нормально!).
(устно проверяем, что с другим пределом интегрирования всё нормально!).

Добавка  обозначает, что предел у нас левосторонний, и к точке
обозначает, что предел у нас левосторонний, и к точке  мы приближаемся по оси
мы приближаемся по оси  слева.
слева.
Разбираемся, почему дробь
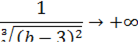
Подставляем под корень предельное значение  :
:
 и тогда
и тогда 
Окончательно:

Несобственный интеграл расходится.
Знак минус обозначает, что соответствующая криволинейная трапеция расположена под осью  .
.
- Абсолютная сходимость
Интеграл
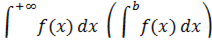
называется абсолютно сходящимся, если

сходится.
Если интеграл сходится абсолютно, то он сходится.
- Условная сходимость
Интеграл  называется условно сходящимся, если
называется условно сходящимся, если 
сходится, а  расходится.
расходится.
o Теорема о сходимости
Если  и
и  сходится к числу, то и
сходится к числу, то и 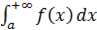 сходится к числу, если же
сходится к числу, если же  расходится, то и
расходится, то и  также расходится.
также расходится.
Пример:


Контрольные вопросы:
1. Какой определенный интеграл называется несобственным?
2. Какие виды несобственных интегралов вы знаете?
3. Каков геометрический смысл несобственного интеграла 1-го типа?
4. Условия абсолютной и условной сходимости.
5. Сформулировать теорему о сходимости. Приведите пример.
ЛЕКЦИЯ 21:
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
План лекции
1. Функции нескольких переменных. Область определения. Непрерывность.
2. Частные производные.
3. Графики простейших функций.
- Определение функции нескольких переменных
При рассмотрении многих вопросов из различных областей знания приходится изучать такие зависимости между переменными величинами, когда числовые значения одной из них полностью определяются значениями нескольких других.
Например, изучая физическое состояние какого-либо тела, приходится наблюдать изменение его свойств от точки к точке. Каждая точка тела задается тремя координатами:  Поэтому, изучая, скажем, распределение плотности, заключаем, что плотность тела зависит от трех переменных:
Поэтому, изучая, скажем, распределение плотности, заключаем, что плотность тела зависит от трех переменных:  Если физическое состояние тела к тому же еще и меняется с течением времени
Если физическое состояние тела к тому же еще и меняется с течением времени  , то та же плотность будет зависеть уже от значений четырех переменных:
, то та же плотность будет зависеть уже от значений четырех переменных:  .
.
Другой пример: изучаются издержки производства на изготовление единицы некоторого вида продукции. Пусть:
 затраты по материалам,
затраты по материалам,
 расходы на выплату заработной платы работникам,
расходы на выплату заработной платы работникам,
 амортизационные отчисления.
амортизационные отчисления.
Очевидно, что издержки производства зависят от значений названных параметров 
Определение:
Если каждой совокупности значений "  " переменных
" переменных  из некоторого множества
из некоторого множества  этих совокупностей соответствует своё единственное значение переменной
этих совокупностей соответствует своё единственное значение переменной  , то говорят, что на множестве
, то говорят, что на множестве  задана функция:
задана функция:  "
"  " переменных.
" переменных.
Множество  , указанное в определении, называется областью определения или областью существования этой функции.
, указанное в определении, называется областью определения или областью существования этой функции.
Если рассматривается функция двух переменных, то совокупности чисел  обозначаются, как правило,
обозначаются, как правило,  и интерпретируются как точки координатной плоскости
и интерпретируются как точки координатной плоскости  , а область определения функции
, а область определения функции  двух переменных изобразится в виде некоторого множества точек на плоскости
двух переменных изобразится в виде некоторого множества точек на плоскости  .
.
Так, например, областью определения функции:  является множество точек плоскости
является множество точек плоскости  , координаты которых удовлетворяют соотношению
, координаты которых удовлетворяют соотношению 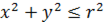 , т. е. представляет собой круг радиуса
, т. е. представляет собой круг радиуса  с центром в начале координат.
с центром в начале координат.
Для функции  областью определения служат точки, которые удовлетворяют условию
областью определения служат точки, которые удовлетворяют условию 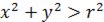 , т. е. внешние по отношению к заданному кругу.
, т. е. внешние по отношению к заданному кругу.
Часто функции двух переменных задаются в неявном виде, т. е. как уравнение  , связывающее три переменные величины. В этом случае каждую из величин
, связывающее три переменные величины. В этом случае каждую из величин  можно рассматривать как неявную функцию двух остальных.
можно рассматривать как неявную функцию двух остальных.
Геометрическим изображением (графиком) функции двух переменных  является множество точек
является множество точек  в трехмерном пространстве
в трехмерном пространстве  , координаты которых удовлетворяют уравнению
, координаты которых удовлетворяют уравнению  .
.
Графиком функции непрерывных аргументов, как правило, является некоторая поверхность в пространстве  , которая проектируется на координатную плоскость
, которая проектируется на координатную плоскость  в область определения функции
в область определения функции  .
.
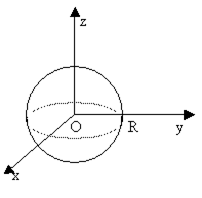
Так, например, графиком функции  является верхняя половина сферы, а графиком функции
является верхняя половина сферы, а графиком функции  нижняя половина сферы.
нижняя половина сферы.
Графиком линейной функции  является плоскость в пространстве
является плоскость в пространстве 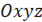 , а графиком функции
, а графиком функции  служит плоскость, параллельная координатной плоскости
служит плоскость, параллельная координатной плоскости  .
.
Заметим, что функцию трех и большего числа переменных изобразить наглядно в виде графика в трехмерном пространстве невозможно.
Основные поверхности:
- Уравнение эллиптического параболоида в каноническом виде:


- Каноническое уравнение эллиптического конуса имеет вид:


- Каноническое уравнение однополостного гиперболоида имеет вид:


- Каноническое уравнение двуполостного гиперболоида имеет вид:


- Уравнение гиперболического цилиндра имеет вид:


- Непрерывность функции двух переменных
Пусть функция  определена в точке
определена в точке  и её окрестности.
и её окрестности.
Определение
Функция называется непрерывной в точке 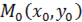 , если
, если  .
.
Если функция  непрерывна в точке
непрерывна в точке  , то
, то

Поскольку
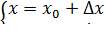

То есть, если функция  непрерывна в точке
непрерывна в точке  , то бесконечно малым приращениям аргументов в этой области соответствует бесконечно малое приращение
, то бесконечно малым приращениям аргументов в этой области соответствует бесконечно малое приращение  функции
функции  .
.
Справедливо и обратное утверждение: если бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции, то функция непрерывна.
Функцию, непрерывную в каждой точке области, называют непрерывной в области.
Пример 1:
Исследовать на непрерывность функцию
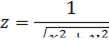
Решение:
Данная функция определена при всех значениях переменных  и
и  , кроме начала координат, где знаменатель обращается в ноль.
, кроме начала координат, где знаменатель обращается в ноль.
Многочлен 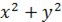 непрерывен всюду, а значит и непрерывен корень квадратный из непрерывной функции.
непрерывен всюду, а значит и непрерывен корень квадратный из непрерывной функции.
Дробь же будет непрерывной всюду, кроме точек, где знаменатель равен нулю. То есть рассматриваемая функция непрерывна на всей координатной плоскости  , исключая начало координат.
, исключая начало координат.
Пример 2:
Исследовать на непрерывность функцию

Решение:
Тангенс определен и непрерывен при всех конечных значениях аргумента, кроме значений, равных нечетному числу величины  , т.е. исключая точки, где
, т.е. исключая точки, где

При каждом фиксированном 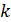 уравнение определяет гиперболу. Поэтому рассматриваемая функция является непрерывной функцией
уравнение определяет гиперболу. Поэтому рассматриваемая функция является непрерывной функцией  и
и  , исключая точки, лежащие на кривых.
, исключая точки, лежащие на кривых.
o Частные производные
Если существует конечный предел отношения частного приращения по  функции
функции  в точке
в точке  к вызвавшему его приращению
к вызвавшему его приращению  при
при 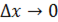 ,
,

то этот предел называется частной производной по 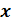 функции
функции  в точке
в точке  и обозначается одним из символов:
и обозначается одним из символов:

- Пример:

Решение:


Контрольные вопросы:
1. Что такое функция двух переменных?
2. Что такое геометрическое изображение функции двух переменных?
3. Перечислить названия основных поверхностей и их канонические уравнения.
4. Какая функция называется непрерывной?
5. Что называется частной производной?
ЛЕКЦИЯ 22:
ФОРМУЛА ПРИРАЩЕНИЙ
План лекции
1. Формула приращений. Дифференциал.
2. Сложные функции нескольких переменных и их дифференцирование.
o Формула приращений
 | |||
 | |||













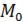













Формула приращения:

o Дифференциал
Дифференциалом функции  в точке x, соответствующим приращению аргумента D x, называют главную линейную относительно D x часть приращения этой функции в точке x.
в точке x, соответствующим приращению аргумента D x, называют главную линейную относительно D x часть приращения этой функции в точке x.
Принято обозначать дифференциал функции  символом
символом  ,
,
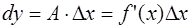 .
.

Если функция  дифференцируема в точке
дифференцируема в точке  из ее области определения
из ее области определения  , то линейная относительно приращений
, то линейная относительно приращений  часть полного приращения функции, то есть величина
часть полного приращения функции, то есть величина

называется дифференциалом функции 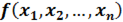 в точке
в точке  и обозначается
и обозначается  .
.
Пусть на области  задана функция двух переменных
задана функция двух переменных  ,
,  - внутренняя точка области
- внутренняя точка области 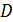 ,
,  - "соседняя" с
- "соседняя" с 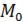 точка из
точка из 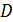 .
.
Рассмотрим полное приращение функции:

Если 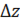 представлено в виде:
представлено в виде:
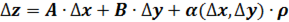
где  - постоянные (не зависящие от
- постоянные (не зависящие от  ),
),  - расстояние между
- расстояние между  и
и 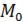 ,
,  - бесконечно малая при
- бесконечно малая при  ; тогда функция
; тогда функция 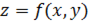 называется дифференцируемой в точке
называется дифференцируемой в точке  , а выражение
, а выражение

называется полным дифференциалом функции  в точке
в точке  .
.
Теорема:
Если  дифференцируема в точке
дифференцируема в точке 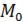 , то
, то

o Сложные функции нескольких переменных и их дифференцирование
Функцией  переменных называется отображение некоторого множества
переменных называется отображение некоторого множества  во множество вещественных чисел
во множество вещественных чисел  . Иначе говоря, функция - это правило, по которому
. Иначе говоря, функция - это правило, по которому  ставится в соответствие вещественное число
ставится в соответствие вещественное число  . Это правило (соответствие) обозначают:
. Это правило (соответствие) обозначают:  или
или  .
.
Множество  называется областью определения функции, а множество
называется областью определения функции, а множество  - областью значений функции
- областью значений функции  .
.
Замечание:
Если  , то
, то  - функция двух переменных. Чаще для функции двух переменных используют обозначение
- функция двух переменных. Чаще для функции двух переменных используют обозначение 
В трехмерном евклидовом пространстве с введенной декартовой системой координат функция  задает некоторую поверхность. Например, функция
задает некоторую поверхность. Например, функция  задает параболоид вращения
задает параболоид вращения

Для непрерывных функций  переменных справедливы следующие теоремы:
переменных справедливы следующие теоремы:
Теорема 1
Функция  , непрерывная на замкнутом и ограниченном множестве
, непрерывная на замкнутом и ограниченном множестве  , ограничена на этом множестве и достигает на нем своего наибольшего и наименьшего значений.
, ограничена на этом множестве и достигает на нем своего наибольшего и наименьшего значений.
Теорема 2
Пусть функция  непрерывна в замкнутом и ограниченном множестве
непрерывна в замкнутом и ограниченном множестве  и пусть
и пусть  для всех точек
для всех точек  . Если для числа
. Если для числа  справедливо неравенство
справедливо неравенство  , то существует точка
, то существует точка 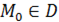 , такая, что
, такая, что  .
.
Если существует конечный предел отношения частного приращения по  функции
функции  в точке
в точке 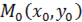 к вызвавшему его приращению
к вызвавшему его приращению  при
при 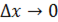 ,
,

то этот предел называется частной производной по  функции
функции  в точке
в точке  и обозначается одним из символов:
и обозначается одним из символов:

Для сложной функции двух переменных 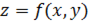 , где
, где 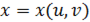 и
и  , частные производные по независимым переменным
, частные производные по независимым переменным  и вычисляются по формулам:
и вычисляются по формулам:
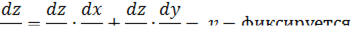

Примеры:
1) 
Решение:


(при дифференцировании по  мы считаем
мы считаем  , а при дифференцировании по
, а при дифференцировании по  мы считаем
мы считаем  ).
).
2) 
Решение:



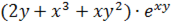
3) 
Решение:
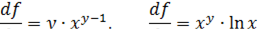
Первая из них вычисляется как производная степенной функции от  (при
(при  ),
),
а вторая - как производная показательной функции от  (при
(при  ).
).
Контрольные вопросы:
1. Сформулировать формулу приращений.
2. Что такое дифференциал функции?
3. Как дифференцируются сложные функции нескольких переменных?
ЛЕКЦИЯ 23: