План лекции
1. Оператор Лапласа в полярной системе координат.
2. Понятие о волновом уравнении.
3. Падающая и отраженная волна.
o Оператор Лапласа в полярной системе координат
Оператор Лапласа — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом  . Функции
. Функции 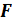 он ставит в соответствие функцию
он ставит в соответствие функцию

Оператор Лапласа эквивалентен последовательному взятию операций градиента и дивергенции:  , таким образом, значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального векторного поля
, таким образом, значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального векторного поля 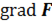 в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом
в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом 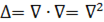 , то есть в виде скалярного произведения оператора набла на себя. Оператор Лапласа унитарен.
, то есть в виде скалярного произведения оператора набла на себя. Оператор Лапласа унитарен.
Уравнение Лапласа — дифференциальное уравнение в частных производных. В трёхмерном пространстве уравнение Лапласа записывается так:

Уравнение рассматривают также в двумерном и одномерном пространстве. В двумерном пространстве уравнение Лапласа записывается:
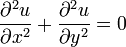
В полярных координатах 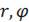 уравнение Лапласа имеет вид:
уравнение Лапласа имеет вид:

o Понятие о волновом уравнении
Волновое уравнение — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно линейная: звук в газах, жидкостях и твёрдых телах) и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн. Является одним из основных уравнений математической физики.
В многомерном случае однородное волновое уравнение записывается в виде:

где  — оператор Лапласа,
— оператор Лапласа,  — неизвестная функция,
— неизвестная функция,  — время,
— время,  — пространственная переменная,
— пространственная переменная, 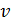 — фазовая скорость.
— фазовая скорость.
Вывод для трёхмерного случая: в одномерном случае уравнение называется также уравнением колебания струны или уравнением продольных колебаний стержня и записывается в виде:

Разность  называется оператором Даламбера и обозначается как
называется оператором Даламбера и обозначается как  . Таким образом, с использованием оператора Даламбера однородное волновое уравнение записывается как:
. Таким образом, с использованием оператора Даламбера однородное волновое уравнение записывается как:

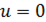
Допустимо также рассматривать неоднородное волновое уравнение:
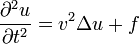
где 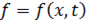 — некая заданная функция внешней силы.
— некая заданная функция внешней силы.
Стационарным вариантом волнового уравнения является уравнение Лапласа (уравнение Пуассона в неоднородном случае).
Задача нахождения нормальных колебаний системы, описываемой волновым уравнением, приводит к задаче на собственные значения для уравнения Лапласа, то есть к нахождению решений уравнения Гельмгольца, получающегося подстановкой
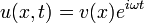 или
или 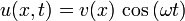 .
.
o Падающая и отраженная волна
Длинная линия — регулярная линия электропередачи, длина которой превышает длину волны колебаний, распространяющихся в ней, а расстояние между проводниками, из которых она состоит, значительно меньше этой длины волны.
Характерной особенностью длинных линий является проявление интерференции двух волн, распространяющихся навстречу друг другу. Одна из этих волн создается подключенным к линии генератором электромагнитных колебаний, и называется падающей. Другая волна называется отражённой, и возникает из-за отражения падающей волны от нагрузки, подключенной к противоположному концу линии. Все разнообразие процессов, происходящих в длинной линии, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами.
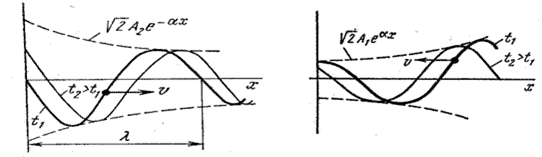
*Слева – падающая волна, справа – отраженная
Физически эффект уменьшения амплитуд падающей и отраженной волн по мере их продвижения по линии объясняется наличием потерь в линии.
На рисунке слева изображены графики распределения падающей волны напряжения вдоль линии (в функции  ) для двух смежных моментов времени:
) для двух смежных моментов времени: 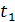 и
и 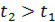 . Падающая волна распространяется слева направо. При построении принято
. Падающая волна распространяется слева направо. При построении принято  .
.
На рисунке справа представлены графики распределения отраженной волны напряжения для двух смежных моментов времени: 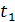 и
и 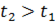 .
.
Отраженная волна распространяется справа налево.
Отношение напряжения отраженной волны в конце линии к напряжению падающей волны в конце линии называют коэффициентом отражения по напряжению и обозначают 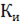 .
.
Фазовой скоростью  называют скорость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу колебания, или иначе: фазовая скорость - это скорость перемещения по линии неизменного фазового состояния.
называют скорость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу колебания, или иначе: фазовая скорость - это скорость перемещения по линии неизменного фазового состояния.
Волновое уравнение:

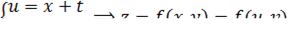
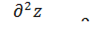
падающая волна



отраженная волна
Пример падающей волны:

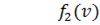








 1
1
0 1 2 
Снимок волны при  , при
, при 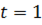 . Если
. Если  ,
,  , если
, если 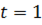 , то
, то 

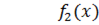








 1
1
1 2 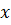













 1
1
0 1 2 3 
Скорость волны – 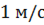 .
.
Контрольные вопросы:
1. Что такое оператор Лапласа? Уравнение Лапласа? Как записывается уравнение Лапласа в полярных координатах?
2. Что называется волновым уравнением? Как записывается волновое уравнение?
3. Что такое оператор Даламбера?
4. Что называется длинной линией, отраженной волной, падающей волной?
5. Что такое коэффициент отражения по напряжению?
6. Дать определении фазовой скорости?
II СЕМЕСТР
ЛЕКЦИЯ 1: