· Определение
· Параметрическая форма
· Свойства
Поверхностный интеграл второго рода
· Определение
Связь между поверхностными интегралами второго и первого рода:
Свойства:
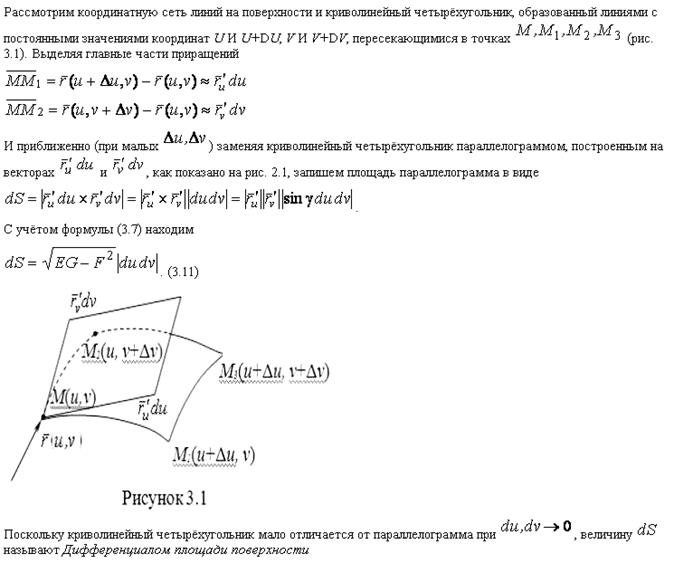
· Дифференциал площади поверхности
· Приложения поверхностных интегралов к задачам геометрии и физики.
Теоретические вопросы
1. Как определяется поверхностный интеграл?
2. Как вычисляется дифференциал площади поверхности?
3. Как вычисляется поверхностный интеграл?
ЛЕКЦИЯ 6:
КОМПЛЕКСНЫЕЧИСЛА
План лекции
1. Основные понятия.
2. Геометрическое изображение комплексных чисел.
3. Тригонометрическая и показательная формы комплексного числа.
4. Действия над комплексными числами.
5. Извлечение корня из комплексного числа
Основные понятия
Определение 1. Комплексным числом называется выражение вида z=x+iy, где х,у – действительные числа, а i – мнимая единица, i2= - 1.
Если х= 0, то число 0+ iy называется чисто мнимым; если у =0, то число х+i 0= х отождествляется с действительным числом х.
Множество R всех действительных чисел является подмножеством множества С всех комплексных чисел, т.е. R Ì C.
Число х называется действительной частью комплексного числа z и обозначается x=Rez, а у – мнимой частью z, y=Imz.
Определение 2. Два комплексных числа z1=x1+iy1 и z2=x2+iy2 называются равными (z1=z2) тогда и только тогда, когда равны их действительные части и равны их мнимые части: х1=х2, у1=у2. В частности, комплексное число z=x+iy равно нулю тогда и только тогда, когда х=у= 0.
Определение 3. Два комплексных числа z=x+iy и 
=x-iy называются сопряженными.
Геометрическое изображение комплексных чисел
Комплексное число z=x+iy можно изобразить точкой М(х;у) плоскости ХОУ, где x=Rez, y=Imz. И наоборот, каждую точку М(х;у) координатной плоскости можно рассматривать как образ комплексного числа z=x+iy (рис.1).
Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, так как на ней лежат действительные числа z=x+0i=х. Ось ординат называется мнимой осью, на ней лежат чисто мнимые комплексные числа z=0+iy.
Комплексное число z=x+iy можно задавать с помощью радиус-вектора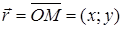 
.
Определение 4. Длина вектора 
, изображающего комплексное число z, называется модулем этого числа и обозначается |z|.
Определение 5. Величина угла между положительным направлением действительной оси и вектором , изображающим комплексное число, называется аргументом этого комплексного числа, обозначается Argz или j.
Аргумент комплексного числа z =0 не определен. Аргумент комплексного числа z¹ 0 определяется с точностью до слагаемого 2pk (k=0,±1,±2,…): Аrgz=argz+ 2pk, где argz – главное значение аргумента, заключенное в промежутке [0;2p].
Тригонометрическая и показательная формы
Комплексного числа
Запись комплексного числа в виде z=x+iy называется алгебраической формой.
Модуль и аргумент комплексного числа можно рассматривать как полярные координаты вектора 
(рис.1). Тогда 
и комплексное число z=x+iy можно записать в виде z = 
= 
. Такая запись комплексного числа называется тригонометрической формой. Модуль 
определяется по формуле 
, аргумент j определяется из формулы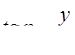 
при этом 
Argz = argz+ 2pk, argz = 
Используя формулу Эйлера 
комплексное число z можно записать в показательной форме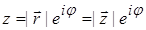 
.