Ранее было доказано, что для нахождения общего решения линейного неоднородного уравнения достаточно знать общее решение соответствующего однородного уравнения и какое-либо частное решение неоднородного уравнения. Для диф. уравнений с постоянными коэффициентами и со спец. правой частью эта задача нами решена.
Рассмотрим метод, позволяющий находить частное решение неоднородного уравнения, если известно общее решение соответствующего однородного уравнения.
Пусть дано уравнение
a 0 (x)y"+a 1 (x)y'+a 2 (x)y=b(x) (*)
Пусть yoo=c 1 y 1 (x)+c 2 y 2 (x) (**)
где y 1 (x) и y 2 (x) – частные решения, образующие фундаментальную систему.
Будем искать решение неоднородного уравнения (*) точно в таком же виде, что и решение (**) для этого подберем c 1 (x) и c 2 (x) так, чтобы выражение (**) являлось бы решением уравнения (*).
y=c 1 (х)y 1 (x)+c 2 (х)y 2 (x) (***), т.е. при подстановке ф-ции (***) и всех ее производных в ур-ние (*) должно получиться тождество
y'x=c' 1 y 1 +c 1 y' 1+ c' 2 y 2 (x)+c 2(х) y' 2(x). Здесь две новые неизвестные ф-ции c 1(х) и c 2(х). Для их определения нужно составить систему из двух ур-ний. В качестве одного из них возьмем такое y=c' 1 (х)y 1 (x)+c' 2 (х)y 2 (x) =0, тогда упростится выражение для y'x: y'x=c 1 y' 1 +c 2 y’ 2 (****)
y"x=c' 1 y' 1 +c 1 y" 1+ c' 2 y' 2 +c 2 y" 2. (*****)
Подставляя выражение (*****), (****), (***) в уравнение (*) получим
a 0 (x) [ c' 1 y' 1 +c 1 y" 1+ c' 2 y' 2 +c 2 y" 2]+ a 1 (x) [ c 1 y' 1 +c 2 y’ 2]+ a 2 (x) [ c 1 y 1 +c 2 y 2]= b(x)
Сгруппируем члены иначе:
[ a 0 y" 1 +a 1 y' 1 +a 2 y 1] c 1 + [ a 1 (x)y" 2 +a 1 (x)y' 2 +a 2 (x)y 2] c 2 +a 0 (x) [ c' 1 y' 1 +c' 2 y' 2] =b(x)
Две скобки обращаются в 0, т.к. у 1(х) и у 2(х) - решение исходного однородного ур-я, тогда c' 1 y' 1+ c' 2 y' 2= 
– это второе уравнение для определения c 1 (х) и c 2 (х):
– опред-ль Вронского.
Пример. y"+ 4 y= 
.
y"+ 4 y =0
k 2+4=0, k 1,2=±2 i
yoo=c1sin 2 x+c2cos 2 x
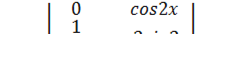
yон=c 1 sin 2 x+c 2 cos 2 x+ 
sin 2 x+ 
cos 2 xln|cos 2 x|.
В общем случае для дифференциального уравнения n-го порядка метод вариации произвольной постоянной имеет вид:
y(n)+p1(x)yn-1+…+pn(x)y=f(x)
y= c 1 y 1 +c 2 y 2+…+ cnyn
y= c 1(x) y 1 +c 2(x) y 2+…+ cn(x)yn
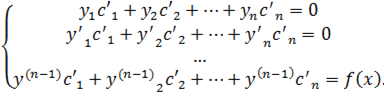
Физические приложения дифференциальных уравнений
В курсах теоретической механики и физики будет показана, что колебательные процессы описываются дифференциальными уравнениями второго порядка с постоянными коэффициентами и со специальными правыми частями.
Теоретические вопросы
1. Как формулируется метод вариации произвольных постоянных?
2. В чем заключаются физические приложения дифференциальных уравнений.
ЛЕКЦИЯ 11:
НОРМАЛЬНЫЕ СИСТЕМЫДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
План лекции
1. Нормальные системы дифференциальных уравнений.
2. Метод исключения.
3. Матричный метод.
Нормальные системы дифференциальных уравнений.
Основные понятия
Определение. Системой ДУ называется совокупность ДУ, каждое из которых содержит независимую переменную, искомую функцию и их производные.
Общий вид системы ДУ первого порядка, содержащей n искомых функций у1,…,уn, следующий:
Система ДУ первого порядка, разрешенных относительно производных (нормальная система) имеет вид:
(1)
где число уравнений равно числу неизвестных.
Определение. Решением системы (1) называется совокупность из n функций у1,…,уn, удовлетворяющих каждому из уравнений этой системы.
Начальные условия для системы (1) имеют вид
у1 (х0)=у10; у2 (х0)=у20;…; уn (х0)=уn0 . (2)
Определение. Решение системы (1) с начальными условиями (2) называют решением задачи Коши.
Условия существования и единственности решения задачи Коши описывает теорема, которую приводим без доказательства.
Теорема (Коши). Если в системе (1) все функции fi(x; y1;…;yn) непрерывны вместе со всеми частными производными по уi в некоторой области D ((n +1) – мерного пространства), то в каждой точке М0(х0;у10;…;уn0) этой области существует, и притом единственное решение системы (1), удовлетворяющее начальным условиям (2).