Ряд

Где

и последовательность  — положительна и монотонна (начиная с некоторого места, хотя бы в широком смысле слова), называется рядом Абелева типа.
— положительна и монотонна (начиная с некоторого места, хотя бы в широком смысле слова), называется рядом Абелева типа.
Теорема (признак Дирихле сходимости рядов Абелева типа)
Пусть выполнены условия:
· Последовательность частичных сумм
 ограничена, то есть
ограничена, то есть
 .
· .
·  .
· .
·  .
Тогда ряд .
Тогда ряд
 сходится. сходится.
|
· Признак Дирихле сходимости рядов Абелева типа является аналогом признака Дирихле о сходимости несобственного интеграла первого рода.
· Легко убедиться, что признак Лейбница сходимости знакопеременных рядов является частным случаем этой теоремы, а именно:


сходимость ряда Лейбница на основании признака Дирихле.
· Оценка остатка ряда Абелева типа.
Рассмотрим ряд

и пусть выполнены условия признака Дирихле. Тогда имеет место оценка:
 .
.
Теоретические вопросы
1. Что называется рядом Фурье?
2. В чем заключается теорема Дирихле о сходимости рядов Фурье?
ЛЕКЦИЯ 17:
РЯДЫФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ
План лекции
3. Ряды Фурье для четных и нечетных функций.
4. Связь рядов Фурье с интегралом Фурье.
§ Ряд Фурье для четных и нечетных функций
Ряд Фурье для нечетной функции содержит только члены с синусом, а для четной функции только свободный член и член с косинусом. Докажем это утверждение в общем виде.
Лемма 1.
Если интегрируемая функция  , четная, то
, четная, то
 , (1)
, (1)
а если нечетная, то
 (2)
(2)
Доказательство:

Сделаем замену  . Тогда
. Тогда
 ,
,
и поэтому
 (3)
(3)
(в последнем интеграле переменная интегрирования снова обозначена буквой  ). Из формулы (3) следует, что если
). Из формулы (3) следует, что если  четная, то справедливо равенство (1), а если нечетная, то равенство (2).
четная, то справедливо равенство (1), а если нечетная, то равенство (2).
ЧТД.
В силу доказанной леммы коэффициенты Фурье для четной  - периодической функции
- периодической функции  вычисляется по формулам
вычисляется по формулам
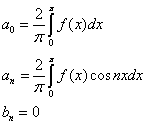 (4)
(4)
так как для любого  функция
функция  четная, а функция
четная, а функция  нечетная. Ряд Фурье четной функции
нечетная. Ряд Фурье четной функции  не содержит членов с синусами:
не содержит членов с синусами:
 ,
,
а коэффициенты вычисляются по формуле (4).
Для четной функции  имеем:
имеем:
 (5)
(5)
так как функция  нечетная, а функция
нечетная, а функция  четная.
четная.
Итак, ряд Фурье нечетной функции не содержит свободного члена и членов с косинусами:

 ,
,
а коэффициенты  вычисляются по формуле (5).
вычисляются по формуле (5).
Заметим, что любую  - периодическую функцию достаточно задать на некотором полуинтервале длины
- периодическую функцию достаточно задать на некотором полуинтервале длины  . В остальных точках она будет определена в силу периодичности. Найдем формулы, выражающие коэффициенты Фурье этой функции через ее значения на произвольном промежутке длины
. В остальных точках она будет определена в силу периодичности. Найдем формулы, выражающие коэффициенты Фурье этой функции через ее значения на произвольном промежутке длины  . Предварительно докажем следующее утверждение:
. Предварительно докажем следующее утверждение:
Лемма 2.
Если  - периодическая с периодом
- периодическая с периодом  функция, то
функция, то

для любого  .
.
Доказательство:
 .
.
Преобразуем последний интеграл:
 ,
,
где мы ввели новую переменную интегрирования  , а в последнем интеграле переменную интегрирования
, а в последнем интеграле переменную интегрирования  обозначили снова буквой
обозначили снова буквой  . Отсюда следует, что интеграл от 0 до T равен интегралу от a до a+T.
. Отсюда следует, что интеграл от 0 до T равен интегралу от a до a+T.
ЧТД.
Согласно лемме 2 из формул (6) пункта 1 находим, что
 (6)
(6)
для любого  , так как функция
, так как функция  и
и  периодические с периодом
периодические с периодом  .
.
Пример:
Найти ряд Фурье для  - периодической функции
- периодической функции  , заданной на промежутке
, заданной на промежутке  формулой
формулой  .
.
Решение.
Вычисляем коэффициенты Фурье по формулам


Таким образом, получаем ряд Фурье:
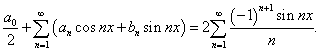
Чтобы показать, что данный ряд Фурье соответствует функции  , будем писать:
, будем писать:

Ответ:















Теоретические вопросы
1. В чем специфика ряда Фурье для четных и нечетных функций?
2. Как определяется интеграл Фурье?