Теорема Лейбница (признак Лейбница) — теорема об условной сходимости знакочередующихся рядов, сформулированная немецким математиком Лейбницем.
Формулировка:
Доказательство:
Следствие:
Доказательство:
· Функциональные последовательности и ряды
Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция 
Функциональная последовательность
Поточечная сходимость
Равномерная сходимость
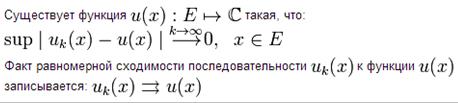
Функциональный ряд
Сходимость
Критерий Коши равномерной сходимости
Абсолютная и условная сходимость
Равномерная сходимость
Признаки равномерной сходимости
Признак сравнения
Признак Дирихле
Признак Абеля
Свойства равномерно сходящихся последовательностей и рядов
Теоремы о непрерывности
Теоремы об интегрировании
Теоремы о дифференцировании
Теоретические вопросы
1. Сходимость знакопеременных рядов: абсолютная и обычная?
2. Теорема Лейбница о сходимости знакочередующихся рядов.
3. Функциональные ряды: определение и примеры.
ЛЕКЦИЯ 15:
СТЕПЕННЫЕ РЯДЫ
План лекции
1. Степенные ряды.
2. Интервал сходимости.
3. Аналитические функции.
4. Ряды Тейлора основных элементарных функций.
5.
· Степенной ряд
Интервал 
, где число 
определено (существует такое 
, что ряд сходится при всех значениях 
, для которых 
и расходится при всех , для которых 
), называется интервалом сходимости ряда
а число – радиусом сходимости этого ряда.
· Пространство степенных рядов
Пространство степенных рядов с одной переменной и коэффициентами из 
обозначается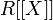 
. Пространство 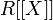имеет структуру дифференциальной алгебры над кольцом (коммутативной, целостной, с единицей, если таково же кольцо ). Оно часто используется в математике ввиду того, что в нём легко представимы и разрешимы формальные дифференциально-алгебраические и даже функциональные соотношения (см. метод производящих функций). При его использовании эти соотношения превращаются в алгебраические уравнения на коэффициенты рядов. Если они разрешаются, говорят о получении формального решения исходной задачи в виде формального степенного ряда.
В 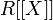определены операции сложения, умножения, формального дифференцирования и формальной суперпозиции. Пусть
Тогда:
(при этом необходимо, чтобы соблюдалось 
)
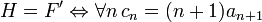
· Сходимость степенных рядов
Из формального степенного ряда с вещественными или комплексными коэффициентами путем приписывания формальной переменной 
какого-нибудь значения в поле вещественных или комплексных чисел можно получить числовой ряд. Числовой ряд считается сходящимся (суммируемым), если сходится последовательность частичных сумм, составленных из его членов, и называется абсолютно сходящимся, если сходится последовательность частичных сумм, составленных из его членов, взятых по модулю (по норме).
· Признаки сходимости
Для степенных рядов есть несколько теорем, описывающих условия и характер их сходимости.
o Первая теорема Абеля:
Пусть ряд 
сходится в точке 
. Тогда этот ряд сходится абсолютно в круге 
и равномерно по 
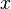на любом компактном подмножестве этого круга.
Обращая эту теорему, получаем, что если степенной ряд расходится при 
, он расходится при всех 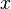, таких что 
. Из первой теоремы Абеля также следует, что существует такой радиус круга (возможно, нулевой или бесконечный), что при 
ряд сходится абсолютно (и равномерно по 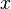на компактных подмножествах круга ), а при 
— расходится. Это значение называется радиусом сходимости ряда, а круг — кругом сходимости.
o Формула Коши-Адамара:
Значение радиуса сходимости степенного ряда может быть вычислено по формуле:
Пусть 
и 
— два степенных ряда с радиусами сходимости 
и 
. Тогда
Если у ряда свободный член нулевой, тогда
Вопрос о сходимости ряда в точках границы 
круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:
o Признак Д’Аламбера:
Если при 
и 
выполнено неравенство
тогда степенной ряд сходится во всех точках окружности абсолютно и равномерно по .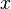
o Признак Дирихле:
Если все коэффициенты степенного ряда положительны и последовательность 
монотонно сходится к нулю, тогда этот ряд сходится во всех точках окружности 
, кроме, быть может, точки 
.
o Вторая теорема Абеля:
Пусть степенной ряд сходится в точке . Тогда он сходится равномерно по 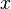на отрезке, соединяющем точки 0 и .
Сумма степенного ряда как функция комплексного параметра 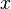является предметом изучения теории аналитических функций.
· Вариации и обобщения
Степенной ряд от n переменных — это формальное алгебраическое выражение вида:
или, в мультииндексных обозначениях,
где — это вектор 
, 
— мультииндекс 
, 
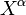— одночлен 
. Пространство степенных рядов от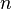 
переменных и коэффициентами из обозначается 
. В нём определены операции сложения, умножения, дифференцирования по каждой переменной и 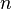-местной суперпозиции. Пусть
Тогда:
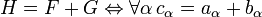
Про пространство можно сказать практически то же самое, что и про .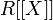
§ Аналитические функции. Ряд Тейлора.
Функция f (x) называется аналитической в точке x 0, если для всех x, удовлетворяющих условию | x – x 0 | < f, функция f (x) есть сумма некоторого степенного ряда:
Каждая аналитическая в точке 
функция аналитична также в некоторой окрестности 
. Сумма, разность и произведение аналитических функций — аналитические функции. Если функция 
— аналитическая в и 
, то функция — также аналитическая в . Функция 
аналитична в , если 
аналитична в и 
аналитична в 
. Если 
аналитична в , то в некоторой окрестности она дифференцируема любое число раз и
Тогда
и
(ряд Тейлора)
Если функция 
в некоторой окрестности точки дифференцируема любое число раз, а остаточный член в формуле Тейлора стремится к нулю при 
, то степенной ряд имеет отличный от нуля радиус сходимости, а функция 
аналитична в .
Эти соображения можно перенести на степенные ряды с большим числом переменных. Функция 
, которую можно записать как сумму степенного ряда от двух переменных:
С областью сходимости точки, отличные от 
называется аналитической в точке 
Точка относится к области сходимости, если степенной ряд в этой точке сходится. Для степенных рядов нескольких переменных имеют место теоремы, аналогичные теоремам для одного переменного.
Теоретические вопросы
1. Дайте определение степенного ряда.
2. Какой вид имеет область сходимости степенного ряда?
3. Что такое ряд Тейлора?
4. Как вычислить область сходимости степенного ряда с помощью признака Даламбера?