План лекции
1. Двойные и тройные интегралы. Определение.
2. Геометрический смысл.
3. Методы вычисления приложения.
· Двойной интеграл. Свойства двойного интеграла. Вычисление двойного интеграла. Геометрический смысл

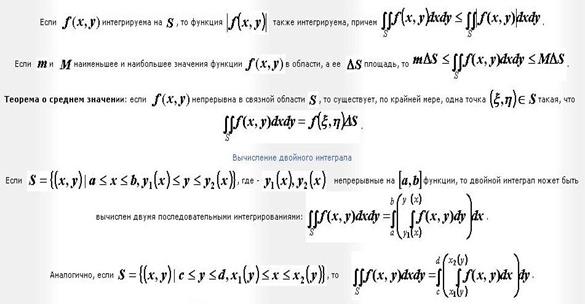

· Тройной интеграл. Свойства тройного интеграла. Вычисление тройного интеграла. Геометрический смысл


ПРИЛОЖЕНИЯ ДВОЙНОГО ИНТЕГРАЛА


ПРИЛОЖЕНИЯ ТРОЙНОГО ИНТЕГРАЛА

Теоретические вопросы
1. Что такое двойной интеграл?
2. Как вычисляется двойной интеграл?
3. Приведите основные свойства двойного интеграла?
4. В чем заключается геометрический смысл двойного интеграла?
5. Что такое тройной интеграл?
ЛЕКЦИЯ 3:
ЗАМЕНА ПЕРЕМЕННЫХ В КРАТНЫХ ИНТЕГРАЛАХ
План лекции
1. Замена переменных в кратных интегралах. Якобиан.
2. Понятие о дифференцируемых отображениях.
· Замена переменных в кратных интегралах

· Якобиан
Якобиан (определитель Якоби, функциональный определитель) — определитель матрицы Якоби:
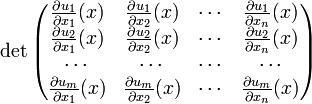
для векторной функции
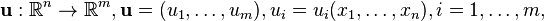
имеющей в некоторой точке все частные производные первого порядка (определитель Якоби или якобиан системы функций 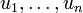 ).
).
Также якобианом иногда (по-русски такое употребление термина не вполне принято) называют саму матрицу Якоби, а не её определитель. По-английски и в некоторых других языках термин якобиан считается равно приложимым к матрице Якоби и её определителю.
· Часто используются следующие обозначения якобиана:
 или
или 
· Определитель Якоби обычно определён для случая m = n, то есть для квадратных матриц Якоби; для m ≠ n его можно считать нулём (в простейшей интерпретации матрица Якоби дописывается при этом нулями до квадратной).
Смысл и применение определителя Якоби

Основные применения

(формула замены переменных в n-мерном интеграле)
· Понятие о дифференцируемых отображениях

Теоретическиевопросы
1. Как осуществить полярную замену переменных в двойном интеграле? Чему равен Якобиан?
2. Как вычислить центр тяжести плоской области?
3. Как вычислить момент инерции для плоской области?
4. Как изменить порядок интегрирования в двойном интеграле?
ЛЕКЦИЯ 4:
ЭЛЕМЕНТЫТЕОРИИ ПОВЕРХНОСТЕЙ
План лекции
1. Элементы теории поверхностей.
2. Параметризованные поверхности.
3. Координатные линии. Касательная плоскость и нормаль.
Поверхность — традиционное название для двумерного многообразия в пространстве.
· Способы задания

· Поверхность в дифференциальной геометрии

Параметры 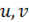 можно рассматривать как внутренние координаты точек поверхности. Фиксируя одну из координат, мы получаем два семейства координатных кривых, покрывающих поверхность координатной сеткой.
можно рассматривать как внутренние координаты точек поверхности. Фиксируя одну из координат, мы получаем два семейства координатных кривых, покрывающих поверхность координатной сеткой.
Случай явного задания. Поверхность  может быть определена как график функции
может быть определена как график функции  ; тогда является гладкой регулярной поверхностью, если функция
; тогда является гладкой регулярной поверхностью, если функция  дифференцируема. Этот вариант можно рассматривать как частный случай параметрического задания:
дифференцируема. Этот вариант можно рассматривать как частный случай параметрического задания: 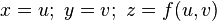 .
.
· Касательная плоскость

· Нормаль

· Понятие о криволинейных координатах. Координатные линии и координатные оси.

Теоретические вопросы
1. Что такое параметризованная поверхность?
2. Приведите основные параметризации сферы, кругового цилиндра, кругового конуса?
3. Дайте определение координатных линий?
ЛЕКЦИЯ 5:
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
План лекции
1. Поверхностные интегралы.
2. Дифференциал площади поверхности.
3. Приложения поверхностных интегралов к задачам геометрии и физики.