Доказательство.
Введем обозначение: Pn (x) = f (x 0) + … + 
(x – x 0) n º j (x, x 0). Возьмем " x ¹ x 0 из указанной в условии теоремы окрестности точки x 0. Пусть для определенности x > x 0.
(здесь рисунок)
x – фиксированное. Возьмем какое-нибудь p > 0. Числовую переменную, изменяющуюся на сегменте [ x 0, x ], обозначим буквой t: x 0 £ t £ x, и введем функцию:
y (t) = f (x) - j (x, t) - 
= f (x) - j (x, t) - Rn +1(x).
y (t) на [ x 0, x ] удовлетворяет всем условиям теоремы Ролля:
y (t) = f (x) - [ f (t) +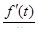 
(x – t) + 
(x – t)2 + … +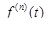 
(x – t) n ] - Rn +1(x).
Так как f (x) n +1 раз дифференцируема, то y (t) непрерывна на [ x 0, x ],
1) y (t) дифференцируема в интервале (x 0, x),
2) y (x 0) = f (x) - j (x, x 0) - 
[ f (x) - j (x, x 0)] = 0,
y (x) = 0, y (x 0) = y (x). По теореме Ролля, $ x Î (x 0, x): y ’(x) = 0.
y ’(t) = - [ f ’(t) - f ’(t) + f ’’(t)(x – t) - f ’’(t)(x – t) + 
(x – t)2 - … + … -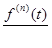 
(x – t) n -1+
+ 
(x – t) n ] + p 
Rn +1(x).
Полагая t = x, получаем:
y ’(x) = 
(x – x) n + p 
Rn +1(x) = 0.
Rn +1(x) =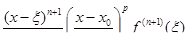 
. (7) Теорема доказана.
Контрольные вопросы:
1. Что такое производная по направлению?
2. Что называется градиентом?
3. Каков геометрический смысл градиента?
4. Запишите формулу Тейлора для функции двух переменных.
ЛЕКЦИЯ 24:
ЭКСТРЕМУМ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
План лекции
1. Экстремум функции нескольких переменных.
2. Необходимые и достаточные условия.
3. Условный экстремум. Функция Лагранжа.
o Экстремум функции нескольких переменных. Необходимые и достаточные условия.
Говорят, что функция 
имеет максимум в точке 
, т.е. при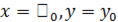 
, если 
для всех точек 
, достаточно близких к точке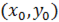 
и отличных от неё.
Говорят, что функция имеет минимум в точке 
, т.е. при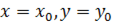 
, если 
для всех точек , достаточно близких к точке 
и отличных от неё.
Максимум и минимум функции называются экстремумами функции.
Теорема (необходимое условие экстремума функции двух переменных).
Если функция достигает экстремума при 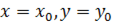, то каждая частная производная первого порядка от 
или обращается в нуль при этих значениях аргументов, или не существует.
Теорема (достаточное условие экстремума функции двух переменных).
Пусть в некоторой области, содержащей точку 
функция имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка является критической точкой функции 
, т.е.
тогда при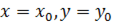 
:
1) 
имеет максимум, если дискриминант 
и 
, где
2) имеет минимум, если дискриминант 
и 
;
3) не имеет ни минимума, ни максимума, если дискриминант 
;
4) если 
, то экстремум может быть, а может и не быть (требуется дополнительное исследование).
Пример:
Исследовать на экстремум функцию 
Решение:
На первом шаге, в соответствии с достаточным условием экстремума функции двух переменных, найдем точки, удовлетворяющие условию:
Частные производные первого порядка от функции равны:
Приравняем их к нулю и решим систему уравнений:
Выпишем отдельно первое уравнение системы и найдем его корни:
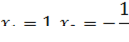
Подставим найденные значения переменной 
во второе уравнение системы:
и 
Таким образом, получили две точки 
и 
, в которых будет продолжено исследование функции на экстремум.
На втором шаге найдем все вторые частные производные от функции :
На третьем шаге для каждой из точек и 
установим наличие экстремума функции (для этого вычислим значения вторых производных и найдем знак дискриминанта 
в указанных точках).
1) Для точки :
Так как дискриминант больше нуля и , то функция 
имеет минимум в точке 
:
2) Для точки :
Так как дискриминант меньше нуля, то функция не имеет в точке ни минимума, ни максимума.
Ответ: в точке функция 
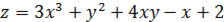имеет минимум 
.
o Условный экстремум функции. Функция Лагранжа
Функция Лагранжа 
динамической системы, названа в честь Жозефа Луи Лагранжа, является функцией обобщённых координат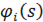 
и описывает эволюцию системы. Например, уравнения движения (для классической механики) в этом подходе получаются из принципа наименьшего действия, записываемого как:
где действие — функционал
а 
— обобщённые координаты (например, координаты частиц или полевые переменные), 
обозначает множество параметров системы.
Функция 
имеет условный максимум (минимум) в точке 
если существует такая окрестность точки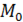 
для всех точек которой, удовлетворяющих уравнениям связи
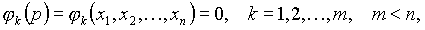
выполняется неравенство 
.
Исследование функции на условный экстремум сводят к исследованию на обычный экстремум функции Лагранжа.
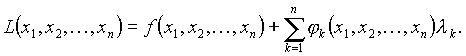
Константы 
называют множителями Лагранжа.
Необходимые условия условного экстремума выражаются системой
Решение системы 
даёт координаты точки (или системы точек), в которой возможен условный экстремум.
Достаточные условия условного экстремума вытекают из исследования на знак 
при условии, что дифференциалы 
удовлетворяют уравнениям:
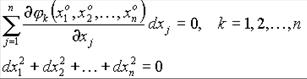
Точнее говоря, функция 
имеет условный максимум (минимум) в точке 
, если для всевозможных наборов выполняется неравенство
Пример:
Найти условный экстремум функции 
, при условии 
Решение:
Составим функцию Лагранжа
Имеем:
Система имеет два решения:
Далее:
При 
поэтому функция 
в точке 
имеет условный минимум, а при 
следовательно, функция имеет в точке 
условный максимум.
Контрольные вопросы:
1. Как вычисляется экстремум функции нескольких переменных?
2. Назовите необходимые и достаточные условия экстремума.
3. Что такое условный экстремум функции? Какова функция Лагранжа?
ЛЕКЦИЯ 25-26: