План лекции
1. Криволинейные интегралы I рода. Определение и вычисление.
2. Основные свойства.
3. Приложения к задачам геометрии и физики.
· Определение
1. Дугу кривой 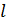 или
или  в пространстве
в пространстве 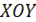 разбиваем на
разбиваем на  малых частей точками
малых частей точками 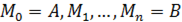 ; обозначаем длины хорд
; обозначаем длины хорд 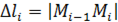 ,
, 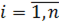 .
.
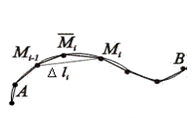
2. Вычисляем значения функции  в произвольно выбираемых точках
в произвольно выбираемых точках 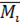 на -той части разбиения и умножаем их на соответствующие длины хорд
на -той части разбиения и умножаем их на соответствующие длины хорд 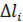 :
: 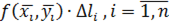
3. Составляем интегральную сумму
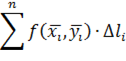
и вычисляем её предел при λ → 0, где λ 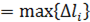 – это ранг разбиения.
– это ранг разбиения.
Если предел интегральной суммы существует, является конечным и не зависит ни от способа разбиения дуги 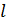 на элементарные части, ни от выбора на них точек
на элементарные части, ни от выбора на них точек 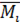 , то он называется криволинейным интегралом I рода от функции
, то он называется криволинейным интегралом I рода от функции 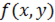 по линии
по линии 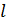 :
:
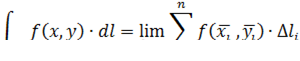
· Механическая трактовка криволинейного интеграла I рода
Если  — это линейная плотность распределения материала по линии
— это линейная плотность распределения материала по линии 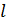 (т.е. количество материала на единицу длины), то
(т.е. количество материала на единицу длины), то

— это «масса» тяжелой линии 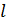 .
.
· Основные свойства криволинейного интеграла I рода
1) Линейность криволинейного интеграла I рода по подынтегральной функции
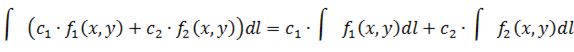
где 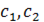 – постоянные по
– постоянные по  .
.
2) Аддитивность криволинейного интеграла I рода по линии интегрирования
Если 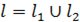 , то
, то
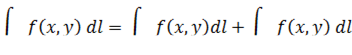
3) Значение криволинейного интеграла I рода от функции, тождественно равной единице на линии интегрирования
Если  на
на  , то
, то
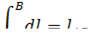
— длина дуги линии  .
.
4) Достаточное условие существования криволинейного интеграла I рода
Если функция 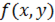 является непрерывной для
является непрерывной для 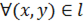 , то
, то
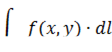
существует.
Вычисление криволинейного интеграла I рода (Как вычисляется криволинейный интеграл I рода)
Если записать параметрические уравнения линии 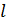 :
:
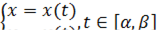
в которых функции 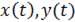 являются дифференцируемыми, то можно показать, что дифференциал длины дуги
являются дифференцируемыми, то можно показать, что дифференциал длины дуги 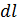 пересчитывается по формуле:
пересчитывается по формуле:
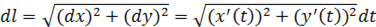
а криволинейный интеграл I рода сводится к определенному интегралу по переменной 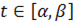 .
.
В результате получается следующая формула для вычисления криволинейного интеграла I рода:
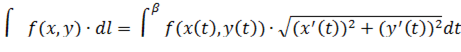
При этом в качестве параметра  на линии
на линии 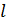 можно брать любую независимую переменную.
можно брать любую независимую переменную.
В частности, если дан двумерный криволинейный интеграл и линия интегрирования 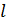 является графиком функции
является графиком функции 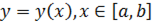 , то в качестве параметра можно взять независимую переменную
, то в качестве параметра можно взять независимую переменную  : тогда
: тогда 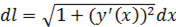 и формула сведения криволинейного интеграла I рода к определенному интегралу будет иметь вид:
и формула сведения криволинейного интеграла I рода к определенному интегралу будет иметь вид:
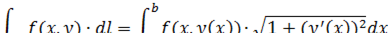
Если плоская линия 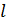 задана уравнением
задана уравнением 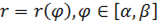 в полярной системе координат, то в качестве параметра нужно брать полярный угол
в полярной системе координат, то в качестве параметра нужно брать полярный угол 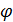 и использовать связь между полярными и декартовыми координатами:
и использовать связь между полярными и декартовыми координатами:  . Тогда
. Тогда
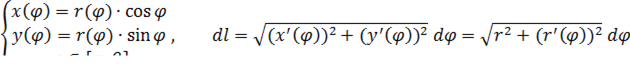
формула сведения криволинейного интеграла I рода к определенному интегралу в полярных координатах:

При составлении 3-x последних формул нужно учитывать, что значение криволинейного интеграла I рода не зависит от направления на линии интегрирования 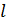 , поэтому
, поэтому  , всегда в следствие этого пределы интегрирования по независимой переменной «от
, всегда в следствие этого пределы интегрирования по независимой переменной «от 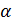 до
до 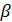 » всегда такие, что
» всегда такие, что 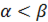 .
.
· Приложения к задачам геометрии и физики
Длина кривой 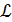 выражается формулой:
выражается формулой:
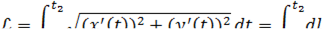
Моменты инерции:
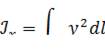
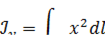
Статические моменты – центры тяжести:

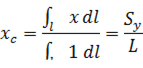
Теоретические вопросы
1. Что такое криволинейный интеграл 1-го рода?
2. Как вычисляется криволинейный интеграл по параметризованной кривой?
3. Как вычислить длину дуги, статистические моменты для кривой?
ЛЕКЦИЯ 2: