ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ

План лекций

1. Производная по направлению.

2. Градиент и его свойства.

3. Формула Тейлора для функции двух переменных.

 

· Производная по направлению

 

Производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.

Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.

Рассмотрим функцию 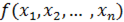от аргументов в окрестности точки . Для любого единичного вектора определим производную функции в точке по направлению следующим образом:

Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора .

Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.

 

· Градиент и его свойства

Градиент — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины , значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении.

Например, если взять в качестве высоту поверхности Земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.

 

С математической точки зрения градиент — это производная скалярной функции, определенной на векторном пространстве.

Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным.

Стандартные обозначения: или, с использованием оператора набла, — вместо может быть любое скалярное поле, обозначенное любой буквой.

Определение

Для случая трёхмерного пространства градиентом скалярной функции координат , , называется векторная функция с компонентами

Или, использовав для единичных векторов по осям прямоугольных декартовых координат :

Если — функция переменных , то её градиентом называется -мерный вектор

компоненты которого равны частным производным по всем её аргументам.

- Размерность вектора градиента определяется, таким образом, размерностью пространства (или многообразия), на котором задано скалярное поле, о градиенте которого идет речь.

- Оператором градиента (обозначаемым обычно, как говорилось выше, или ) называется оператор, действие которого на скалярную функцию (поле) дает ее градиент. Этот оператор иногда коротко называют просто "градиентом".

 

Смысл градиента любой скалярной функции в том, что его скалярное произведение с бесконечно малым вектором перемещения дает полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена , то есть линейную (в случае общего положения она же главная) часть изменения при смещении на . Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:

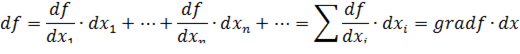
Например, градиент функции 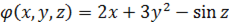будет представлять собой:

 

Геометрический смысл

Рассмотрим семейство линий уровня функции :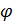

Нетрудно показать, что градиент функции в точке перпендикулярен её линии уровня, проходящей через эту точку. Модуль градиента показывает максимальную скорость изменения функции в окрестности , то есть частоту линий уровня. Например, линии уровня высоты изображаются на топографических картах, при этом модуль градиента показывает крутизну спуска или подъема в данной точке.

 

Связь с производной по направлению

Используя правило дифференцирования сложной функции, нетрудно показать, что производная функции по направлению равняется скалярному произведению градиента 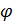на единичный вектор :

Таким образом, для вычисления производной по любому направлению достаточно знать градиент функции, то есть вектор, компоненты которого являются её частными производными.

Операция градиента преобразует холм (слева), если смотреть на него сверху, в поле векторов (справа). Видно, что векторы направлены «в горку» и тем длиннее, чем круче наклон.

o Формула Тейлора для функции двух переменных

 

Пусть функция имеет полные производные вплоть до -го порядка включительно в некоторой окрестности точки . Введём дифференциальный оператор

Тогда разложением Тейлора функции по степеням и в окрестности точки будет

где — остаточный член в форме Лагранжа:

 

В случае функции одной переменной , поскольку для функции одной переменной частная производная тождественно равна полной. Аналогично формула распространяется на функции от любого числа переменных, меняется только число слагаемых в операторе .

 

1) Многочлен Тейлора.

Если дифференцируема в точке x ₀, то ее приращение в этой точке можно представить в виде:

f (x) - f (x ₀) = f ’(x ₀)(x – x ₀) + o (x – x ₀).

f (x) = + o (x – x ₀).

P ₁(x) обладает следующими свойствами: P ₁(x ₀) = f (x ₀), P ’₁(x ₀) = f ’(x ₀). Рассмотрим теперь более общую задачу. Пусть f (x) n раз дифференцируема в точке x ₀, то есть имеет в точке n все производные до n -го порядка. Поставим задачу найти такой многочлен P_n (x) (степени £ n), что:

P_n (x ₀) = f (x ₀), P ’ _n (x ₀) = f ’(x ₀), P ’’ _n (x ₀) = f ’’(x ₀), …, P ^{( n )} _n (x ₀) = f ^{( n )}(x ₀). (1)

Будем искать многочлен P_n (x) в виде:

P_n (x) = a ₀ + a ₁(x – x ₀) + a ₂(x – x ₀)² + a ₃(x – x ₀)³ + … + a_k (x – x ₀) ^k + … + a_n (x – x ₀) ⁿ. (2)

Покажем, что можно так выбрать коэффициенты a ₀, a ₁, …, a_n, что многочлен P_n (x) будет удовлетворять условию (1). Полагая в равенстве (2) x = x ₀ и учитывая первое из равенств (1), получим P_n (x ₀) = a ₀ = f (x ₀). a ₀ = f (x ₀). Продифференцируем равенство (2).

P ’ _n (x) = a ₁ + 2 a ₂(x – x ₀) + 3 a ₃(x – x ₀)² + … + na _n(x – x ₀) ^{n -1}. (2’)

Положим в равенстве (2’) x = x ₀ и учтем второе условие из (1).

P ’ _n (x ₀) = a ₁ = f ( x ₀).

a ₁ = .

Продифференцируем равенство (2’):

P ’’ _n (x) = 2 a ₂ + 2×3 a ₃(x – x ₀) + … + n (n – 1) a _n(x – x ₀) ^{n -1}. (2’’)

Положим в полученном равенстве (2’’) x = x ₀ и учтем третье условие из (1).

P ’’ _n (x ₀) = 2 a ₂ = f ’’(x ₀).

a ₂ = .

И так далее. После k –кратного дифференцирования равенства (2) получим:

P ^(k) _n (x) = k! a_k + 2 a_{k +1}(x – x ₀) + … + n (n - 1)…(n – k + 1)(x – x ₀) ^k. (2^{( k )})

Полагая здесь x = x ₀ и учитывая k +1–е условие из (1), получим:

P ^(k) _n (x ₀) = k! a_k = f ^(k)(x ₀).

a_k = (k = 0, 1, …, n), если принять обозначения f ⁽⁰⁾ = f, 0! = 1. Итак, мы нашли такие коэффициенты a_k, что многочлен

P_n (x) = f (x ₀) + (x – x ₀) + … + (x – x ₀) ⁿ = (x – x ₀) ^k. (3)

удовлетворяет условиям (1). Многочлен (3) называется многочленом Тейлора для функции f (x).

Теорема

Пусть f (x) определена и n +1 раз дифференцируема в окрестности точки x ₀. Пусть x – любое значение аргумента из этой окрестности, не равное x ₀, p – любое вещественное число. Тогда $ точка x Î (x ₀, x):

R_{n +1}(x) = f (x) – P_n (x) = . (7)