План лекции
1. Вычисление площадей и длин дуг в полярной системе координат.
2. Приложение определенного интеграла к решению задач физики.
o Вычисление площади в полярных координатах
Пусть фигура представляет собой сектор, заданный в полярной системе координат кривой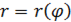 
, где 
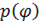- неотрицательная непрерывная кривая на отрезке 
. Разобьем угол 
на 
частей лучами 
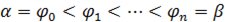и обозначим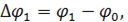 
.
Площадь криволинейного сектора равна сумме площадей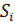 
, заданных разбиением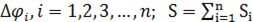 
Выберем один из элементов разбиения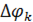 
, соответствующий сектору 
, и зафиксируем на этом промежутке произвольное значение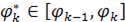 
. Значение функции 
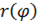в точке 
обозначим и заменим площадь криволинейного сектора круговым сектором радиуса 
, площадь которого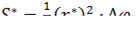 
. Выполним такую же операцию на каждом участке разбиения 
и просуммируем полученные значения.
Сумма площадей круговых секторов:
представляет собой интегральную сумму, предел которой, существующий в силу непрерывности функции 
, равен определенному интегралу, выражающему площадь фигуры в полярных координатах.
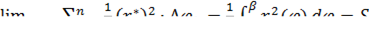
При вычислении площади фигуры в полярных координатах рекомендуется придерживаться такого же порядка исследования, что и в декартовых координатах: построение чертежа, вычисление точек пересечения кривых, образующих границу фигуры; запись формулы.
Пример
Найти площадь фигуры, ограниченной кардиоидой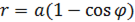 
и окружностью 
.
Решение
Выполним построение фигуры.
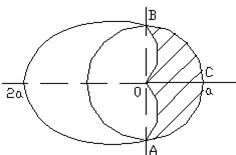
Из рисунка видно, что пересечение кривых образует три различных фигуры: вне круга, вне кардиоиды и внутренняя часть кардиоиды и окружности. Рассмотрим вычисление площади одной из них, расположенной вне кардиоиды (заштрихованная часть на рисунке).
Найдем точки пересечения кривых из системы:
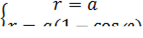
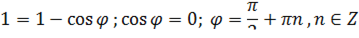
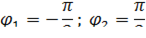
При 
искомая площадь представляет собой часть круга, вырезанного кардиоидой, поэтому следует рассмотреть разность площадей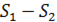 
, где 
- площадь полукруга, а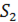 
- площадь, ограниченная кардиоидой и лучами 
.
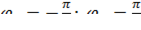Согласно формуле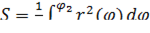 
запишем
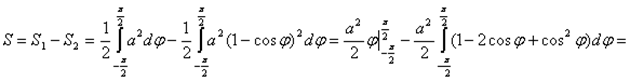
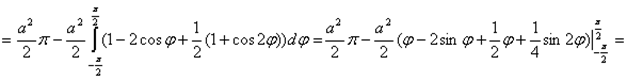
Замечание.
Для вычисления площади, образованной пересечением заданных кривых, расположенной вне круга, надо рассмотреть разность площадей, ограниченных кардиоидой и кругом при
. Для вычисления внутренней части кардиоиды и окружности надо рассмотреть сумму площадей, одна из которых представляет половину круга при , а вторая – сегмент кардиоиды при .
o Длина дуги в полярной системе координат
Когда кривая, ограничивающая область, задана в полярных координатах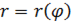 
, то площадь этой области вычисляем по формуле
.
Основная трудность в использовании этой формулы заключается в определении пределов интегрирования 
. Здесь нужно понимать, что кривая 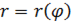определена только, если 
. Поскольку в формуле присутствует 
, то она учтет и не существующую площадь, когда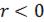 
. Решив уравнение 
, найдем пределы интегрирования.
o Приложения определенного интеграла к решению задач физики.
- Работа переменной силы
Пусть точка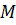 
движется по прямой, причем на перемещении 
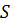на нее вдоль той же прямой действует постоянная сила 
. Из механики известно, что тогда работа этой силы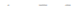 
. Если величина силы непрерывно меняется от точки к точке, то для выражения работы силы снова приходится прибегнуть к интегралу. Пусть путь 
, проходимый точкой, будет независимой переменной.
Предположим, что начальному положению точки 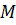соответствует значение 
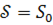, а конечному 
– значение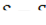 
. Каждому значению в промежутке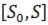 
отвечает определенное положение движущейся точки 
, а также определенное значение величины , которую можно рассматривать как функцию от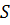 
. Взяв точку в каком-нибудь ее положении, определяемом
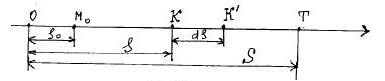
значением пути, найдем теперь приближенное выражение для элемента работы, соответствующего приращению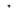 
пути, от 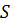до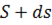 
, при котором точка перейдет в точку 
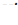(см. рис.). В положении на точку действует сила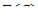 
, поскольку изменение этой величины при переходе точки в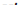 
при малом 
также мало, этим изменением можно пренебречь.
Считая величину силы 
приближенно постоянной, найдем для элемента работы на перемещении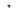 
выражение 
.
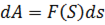Тогда
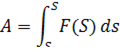
- Путь, пройденный телом
Пусть материальная точка перемещается по прямой с переменной скоростью 
. Найдем путь 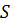, пройденный ею за промежуток времени от 
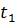до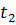 
.
Из физического смысла производной известно, что при движении точки в одном направлении скорость прямолинейного движения равна производной от пути по времени, т. е.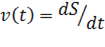 
. Отсюда следует, что 
. Интегрируя полученное равенство в пределах от 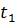до ,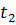
получаем:
Пример
Найти путь, пройденный телом за 4 секунды от начала движения, если скорость тела
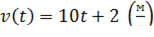
Решение
Если 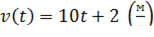, то путь, пройденный телом от начала движения (
) до конца 4-й секунды, равен
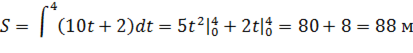
- Давление
Давление, производимое жидкостью с удельным весом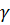 
на одну сторону
погруженной в нее вертикальной пластинки, если расстояние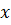 
точек пластинки
до уровня жидкости изменяется от 
до 
(рис.12),
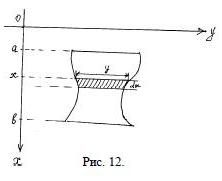
определяется по формуле,
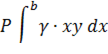
где 
– длина горизонтального сечения пластинки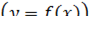 
. Так как на
элементарную пластинку шириной 
давит слой жидкости, находящийся над этой пластинкой, т.е. 
, где 
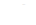– площадь пластинки, 
– объем жидкости, а 
– вес
жидкости, который и оказывает давление. Следовательно, всё давление 
получаем по формуле.
Контрольные вопросы:
1. Как вычислить площадь в полярной системе координат?
2. Как вычислить длину дуга в полярных координатах?
3. Приложения определенного интеграла к решению задач физики.
ЛЕКЦИЯ 20:
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
План лекции
1. Несобственные интегралы. Их типы, сходимость.
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
1. Предел или (или оба предела) являются бесконечными;
2. Функция 
имеет одну или несколько точек разрыва внутри отрезка 
.
- Несобственный интеграл первого типа.
В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так:
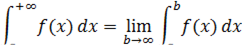
В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: 
.
Реже встречаются интегралы с бесконечным нижним пределом:
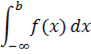
или с двумя бесконечными пределами:
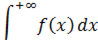
Мы рассмотрим самый популярный случай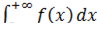 
. Техника работы с другими разновидностями – аналогична. Всегда ли существует несобственный интеграл 
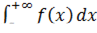? Нет, не всегда.
Подынтегральная функция 
должна быть непрерывной на интервале 
Изобразим на чертеже график подынтегральной функции 
. Типовой график и криволинейная трапеция для данного случая выглядит так:
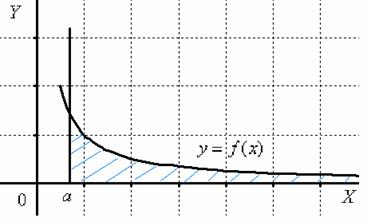
Здесь всё хорошо, подынтегральная функция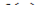 
непрерывна на интервале 
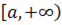, а, значит, несобственный интеграл существует. Обратите внимание, что криволинейная трапеция у нас – бесконечная (не ограниченная справа) фигура.
Несобственный интеграл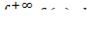 
численно равен площади заштрихованной фигуры, при этом возможны два случая:
1. Первое, мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что, что несобственный интеграл расходится.
2. Но, как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться конечному числу! Например: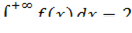 
. Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится.
(Сходимость – когда предел равен числу, расходимость – когда предел равен не числу – либо равен бесконечности, либо не существует)
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции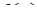 
, и конкретные примеры мы очень скоро рассмотрим. А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл 
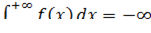(расходится) либо равен отрицательному числу.
Геометрический смысл несобственного интеграла I типа: