Пусть А обозначает матрицу из коэффициентов в правой части системы (1):
,
а решения у1, у2 (координаты коэффициентов радиуса – вектора) составляют матрицу – столбец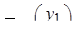 
, тогда систему (1) можно записать в матричной форме:
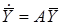, (7)
где справа – произведение матриц.
Решение системы (7) ищем, используя собственные векторы и собственные значения матрицы А, т.е. в виде 
, где l - некоторое число (собственное значение),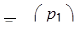 
- собственный вектор.
Подставляем это решение в (7) и сокращая на 
, получим
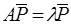. (8)
Система (8) в координатной форме имеет вид:
, (9)
который совпадает с видом системы (6).
Ограничимся случаем действительных различных корней характеристического уравнения матрицы:
. (10)
Пусть l1¹l2 – корни уравнения (10), система (7) допускает два линейно независимых частных решения 
. Общее решение системы (7) получится по формуле
= 
+ 
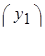или 
, где с 1, с 2 – произвольные константы.
Пример. Решить систему уравнений: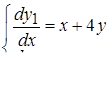 
,
удовлетворяющую начальным условиям: х (0)=1, у (0)=4.
Решение. Выпишем матрицу А и найдем корни ее характеристического уравнения:
Находим координаты собственных векторов:
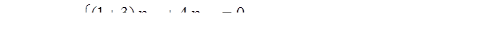
тогда собственный вектор 
.
тогда собственный вектор 
.
Общее решение системы:
= 
+ 
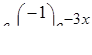или 
,
подставляем начальные условия, находим с 1, с 2:
.
Складываем оба уравнения, имеем 5 с 2=5, с 2=1, 1= - с 1+4, с 1=3.
Частное решение системы:
.
Теоретические вопросы
1. В чем заключается метод исключения?
2. Какая система дифференциальных уравнений называется нормальной?
3. Какие системы решаются с помощью матричного метода?
ЛЕКЦИЯ 12:
ЧИСЛОВЫЕ РЯДЫ.
План лекции
1. Числовые ряды. Сходимость.
2. Простейшие свойства рядов.
3. Простейшие примеры точного суммирования.
4. Необходимое условие сходимости.
Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).
Рассматриваются числовые ряды двух видов
· вещественные числовые ряды — изучаются в математическом анализе;
· комплексные числовые ряды — изучаются в комплексном анализе;
Важнейший вопрос исследования числовых рядов — это сходимость числовых рядов.
Числовые ряды применяются в качестве системы приближений к числам.
Определение
Операции над рядами
Критерий абсолютной сходимости
Определение понятия суммы
Сходимость числовых рядов
Необходимый признак сходимости ряда
Примеры
Теоретические вопросы
1. Что называется числовым рядом?
2. Как определяется n-мерная частичная сумма ряда?
3. Что называется суммой числового ряда?
ЛЕКЦИЯ 13:
СХОДИМОСТЬ РЯДОВ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
План лекции
1. Сходимость рядов с положительными членами.
2. Признак Даламбера.
3. Интегральный признак Коши.
4. Теоремы сравнения.
· Признак Даламбера
Признак сходимости д’Аламбера в предельной форме
Доказательство
Примеры
Теоретические вопросы
1. Как определяется понятие сходимости ряда?
2. В чем заключается необходимое условие сходимости ряда?
3. В чем преимущество исследования сходимости положительных рядов?
4. Сформулируйте признак Даламбера.
5. В чем заключается интегральный признак сходимости Коши?
ЛЕКЦИЯ 14:
ЗНАКОПЕРЕМЕННЫЕ РЯДЫ.
План лекции
1. Знакопеременные ряды. Абсолютная и условная сходимость.
2. Теорема Лейбница.
3. Функциональные последовательности и ряды.
4. Равномерная сходимость.
5. Теоремы Вейерштрасса о почленном дифференцировании функциональных рядов.