1. Математика. Интегральное исчисление. Методические указания к практическим занятиям для студентов I-го курса очной формы обучения по укрупненным группам 11.00.00. «Электроника, радиотехника и системы связи», 15.00.00. «Машиностроение», 13.00.00. «Электро- и Теплоэнергетика», 23.00.00. «Техника и технологии наземного транспорта». – Брянск: БГТУ, 2014г. – 36с.
2. Математика. Дифференциальные исчисления функций одной и нескольких переменных. Методические указания и задачи к практическим занятиям для студентов I курса очной формы обучения по укрупненным группам 11.00.00. «Электроника, радиотехника и системы связи», 15.00.00. «Машиностроение», 13.00.00. «Электро- и Теплоэнергетика», 23.00.00. «Техника и технологии наземного транспорта». – Брянск: БГТУ. – 32с.
РАСЧЕТНО ГРАФИЧЕСКАЯ РАБОТА
I СЕМЕСТР
РГР №1
Задание №1. Исследовать функцию и построить график
| y = ex (2x2-5x+4) | y = 
| ||
y =  (lnx-2) (lnx-2)
| y = 1-  +arctg2x +arctg2x
| ||
y = 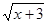 (3,3 +0,2x-0,3x2) (3,3 +0,2x-0,3x2)
| y = ln(x2-x+1) | ||
y = 
| y = ex(2x2+x+1) | ||
y =  -1-arctg(x/2) -1-arctg(x/2)
| y = x3(3lnx-1) | ||
| y = 2x2+5x+ln½x½ | y=  (3,8+1,3x-0,3x2) (3,8+1,3x-0,3x2)
| ||
| y = e-x(2x2+3x+2) | y = 2ln(x2+1)-3arctgx | ||
y = x3/2(lnx- 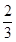 ) )
| y = 0,3x-1-arctg3x | ||
y =  (2,8+0,8x-0,3x2) (2,8+0,8x-0,3x2)
| y = (x2-5) 
| ||
y = 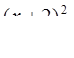
| y = 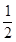 ln(x2+9)- ln(x2+9)-  arctg arctg 
| ||
y = 1-  +arctg(x/3) +arctg(x/3)
| y = x1/3 
| ||
| y = 8x2+10x+ln½x½ | y = 16x-arcsin2x | ||
y =xln(x2+ 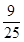 )-2x+ )-2x+  arctg arctg 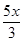
| y = ln(x2-4x+13) | ||
| y = e-x(2x2+9x+11) | y = 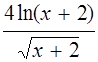
| ||
| y = x2(2lnx-1) | y = 
| ||
y =  (1,7+1,4x-0,3x2) (1,7+1,4x-0,3x2)
| y = 
|
Задание 2

| 
| |||

| 
| |||

| 
| |||

| 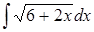
| |||

| 
| |||

| 
| |||

| 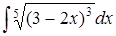
| |||

| 
| |||
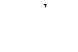
| 
| |||

| 
| |||
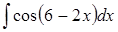
| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
|
Задание 3

| 
| |||

| 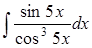
| |||

| 
| |||

| 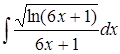
| |||

| 
| |||
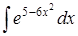
| 
| |||

| 
| |||
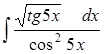
| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
|
Задание 4

| 
| |||

| 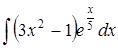
| |||
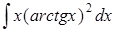
| 
| |||

| 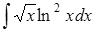
| |||

| 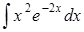
| |||

| 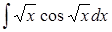
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||
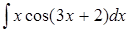
| 
| |||
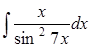
| 
| |||

| 
| |||

| 
|
Задание 5.

| 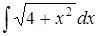
| |||

| 
| |||

| 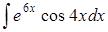
| |||
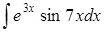
| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||
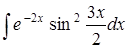
| 
| |||

| 
| |||

| 
| |||
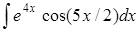
| 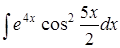
| |||

| 
| |||

| 
| |||

| 
|
Задание 6.
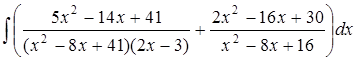
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
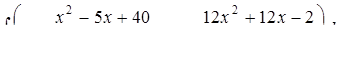
| 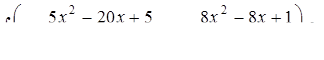
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Задание 7.
1. 
| 2. 
|
3. 
| 4. 
|
5. 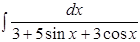
| 6. 
|
7. 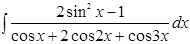
| 8. 
|
9. 
| 10. 
|
11. 
| 12. 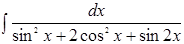
|
13. 
| 14. 
|
15. 
| 16. 
|
17. 
| 18. 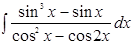
|
19. 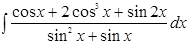
| 20. 
|
21. 
| 22. 
|
23. 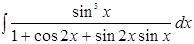
| 24. 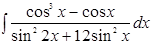
|
25. 
| 26. 
|
27. 
| 28. 
|
29. 
| 30. 
|
31. 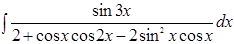
| 32. 
|
33. 
| 34. 
|
Задание 8.
 1 1
| 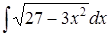
| 
| ||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 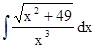
| |||
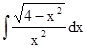
| 
| |||

| 
| |||
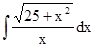
| 
| |||

| 
| |||

| 
| |||

| 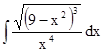
| |||
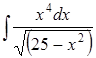
| 
| |||

| 
| |||

| 
| |||

| 
|
Задание 9.
Построить кривую 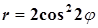 и найти площадь фигуры, ограниченной этой кривой. и найти площадь фигуры, ограниченной этой кривой.
| |
Построить линии  , ,  и найти площадь фигуры, ограниченной этими линиями. и найти площадь фигуры, ограниченной этими линиями.
| |
Кривая  делит круг делит круг  на части. Построить кривую и найти площадь большей части круга. на части. Построить кривую и найти площадь большей части круга.
| |
Построить кривую  и найти площадь фигуры, ограниченной этой кривой. и найти площадь фигуры, ограниченной этой кривой.
| |
Кривая  делит круг делит круг  на две части. Построить кривую и найти отношение площадей частей круга. на две части. Построить кривую и найти отношение площадей частей круга.
| |
Построить кривую  и найти площадь фигуры, ограниченной этой кривой и перпендикуляром к полярной оси (в полюсе). и найти площадь фигуры, ограниченной этой кривой и перпендикуляром к полярной оси (в полюсе).
| |
Построить кривую  и найти площадь фигуры, ограниченной этой кривой и полярной осью. и найти площадь фигуры, ограниченной этой кривой и полярной осью.
| |
Построить линии  , ,  и найти площадь фигуры, ограниченной этими линиями. и найти площадь фигуры, ограниченной этими линиями.
| |
Кривая 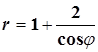 делит круг делит круг  на две части. Построить кривую и найти площадь большей части круга. на две части. Построить кривую и найти площадь большей части круга.
| |
Построить кривую  и найти площадь фигуры, ограниченной этой кривой и полярной осью. и найти площадь фигуры, ограниченной этой кривой и полярной осью.
| |
Построить кривую  и найти площадь фигуры, ограниченной этой кривой. и найти площадь фигуры, ограниченной этой кривой.
| |
Построить кривую 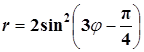 и найти площадь фигуры, ограниченной этой кривой. и найти площадь фигуры, ограниченной этой кривой.
| |
Построить кривую  и найти площадь фигуры, ограниченной этой кривой и перпендикуляром к полярной оси (в полюсе). и найти площадь фигуры, ограниченной этой кривой и перпендикуляром к полярной оси (в полюсе).
| |
Прямая 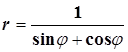 делит фигуру, ограниченную кривой делит фигуру, ограниченную кривой  , на две части. Построить линии и найти площадь меньшей части. , на две части. Построить линии и найти площадь меньшей части.
| |
Кривая  делит круг делит круг  на части. Построить кривую и найти площадь большей части круга. на части. Построить кривую и найти площадь большей части круга.
| |
Построить кривую  и найти площадь фигуры, ограниченной этой кривой и перпендикуляром к полярной оси (в полюсе). и найти площадь фигуры, ограниченной этой кривой и перпендикуляром к полярной оси (в полюсе).
| |
Кривая  делит круг делит круг  на две части. Построить кривую и найти площадь меньшей части круга. на две части. Построить кривую и найти площадь меньшей части круга.
| |
Построить кривую  и найти площадь фигуры, ограниченной этой кривой. и найти площадь фигуры, ограниченной этой кривой.
| |
Построить кривую  и найти площадь фигуры, ограниченной этой кривой. и найти площадь фигуры, ограниченной этой кривой.
| |
Кривая  делит фигуру, ограниченную кривой делит фигуру, ограниченную кривой 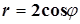 , на три части. Построить кривые и найти отношение площадей частей. , на три части. Построить кривые и найти отношение площадей частей.
| |
Кривая  делит круг делит круг 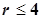 на части. Построить кривую и найти площадь большей части круга. на части. Построить кривую и найти площадь большей части круга.
| |
Прямая  делит фигуру, ограниченную кривой делит фигуру, ограниченную кривой  , на две части. Построить линии и найти площадь меньшей части. , на две части. Построить линии и найти площадь меньшей части.
| |
Кривая  делит фигуру, ограниченную кривой делит фигуру, ограниченную кривой  , на три части. Построить кривые и найти площадь большей части. , на три части. Построить кривые и найти площадь большей части.
| |
Кривая  делит круг делит круг 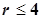 на части. Построить кривую и найти площадь большей части круга. на части. Построить кривую и найти площадь большей части круга.
| |
Построить кривую  и найти площадь фигуры, ограниченной этой кривой и полярной осью. и найти площадь фигуры, ограниченной этой кривой и полярной осью.
| |
Кривая  делит круг делит круг  на две части. Построить кривую и найти отношение площадей частей круга. на две части. Построить кривую и найти отношение площадей частей круга.
| |
Найти площадь внутренней петли кривой  . .
| |
Прямая  делит фигуру, ограниченную кривой делит фигуру, ограниченную кривой  , на две части. Построить линии и найти площадь меньшей части. , на две части. Построить линии и найти площадь меньшей части.
| |
Найти площадь петли кривой 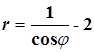 . .
| |
Построить линии  , ,  и найти площадь фигуры, ограниченной этими линиями. и найти площадь фигуры, ограниченной этими линиями.
| |
Найти площадь петли кривой  . .
| |
Построить линии  , ,  и найти площадь фигуры, ограниченной этими линиями. и найти площадь фигуры, ограниченной этими линиями.
|
Задание 10. Исследовать на экстремум функцию двух переменных.
| Z=x3+3x2y+3xy2-12x+15y+2 | Z=x3+6x2y+12xy2-27x+42y-3 | ||
| Z=x3+3xy2+6x2+6y2-18x-18y+1 | Z=y3+3x2y-6x2-6y2-36x-27y+2 | ||
| Z=6xy2-12x2y-y2+54x+48y+1 | Z=4-y3-6xy2-12x2y+30x+27y | ||
| Z=x3+3xy2 -3x2-3y2-48x-24y+2 | Z=x3+3y2x-15x2-15y2+15x-48y | ||
| Z=x3+6x2y+12xy2-3x+18y+3 | Z=x3-3x2y+3xy2-34x-27y+2 | ||
| Z=x3+3y2x-6x2-6y2-27x-36y+4 | Z=y3+3x2y+6x2+6y2-48x-48y+2 | ||
| Z=9xy2-27x2y-y3-27x+12y-2 | Z=2-y3-3xy2-3x2y+36x+12y | ||
| Z=x3+3xy2+3x2 +3y2 -75x-30y+2 | Z=x3+3xy2-6x2-6y2-63x+72y+2 | ||
| Z=x3-6x2y+12xy2-27x+30y+3 | Z=x3+9x2y+27xy2-12x-27y+2 | ||
| Z=x3+3xy2+6x2+6y2-48x-48y+1 | Z=x3+3xy2-6x2-6y2-99x-36y+1 | ||
| Z=-y3-3y2x-3x2y-24x+3y+2 | Z=6xy2-12x2y-y3+18x+3y+2 | ||
| Z=x3+3xy2+3x2+3y2-75x+30y+1 | Z=x3+3xy2-3x2-3y2-108x+36y+2 | ||
| Z=x3-3x2y+3xy2-12x-36y+3 | Z=x3+6x2y+12xy2-48x+54y-2 | ||
| Z=x3+3x2y+6x2+6y2-18x-18y+3 | Z=x3+3y2x-9x2-9y2-57x+38y+3 | ||
| Z=6y2x-12x2y-y3+42x+27y-1 | Z=3xy2-3x2y-y3+15x+12y+1 | ||
| Z=y3+3x2y-3x2-3y2-48y-24x | Z=y3+3x2y-3x2-3y2-108y+36x+2 |
II СЕМЕСТР
РГР№2
Задание №1. Вычислить с помощью двойного интеграла

| |

| |
x= 0,5 y 2, x=y 2, xy =1, xy= 2, z= 2 -x, x,y,z  0, 0, 
| |

| |

| |

| |
y= 2 x, y= 3 x, x+y= 2, x+y= 3,  z= z=  , , 
| |

| |

| |

| |

| |
| |

| |

| |

| |
 , , 
| |

| |
| |

| |
| |
 
| |

| |

| |
xy= 1, xy= 2, x+y= 4, x+y= 3, y > x ³ 0, 
| |

|
Задание №2. Вычислить с помощью тройного интеграла
 , ,  
| |
 , ,  
| |
 , ,  
| |
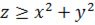 , ,  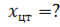
| |
 , ,  
| |
 , ,  
| |
 , ,  
| |
 , ,  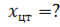
| |
 , ,  
| |
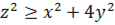 , ,  
| |
 , , 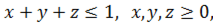 
| |
 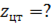
| |
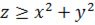 , ,  
| |
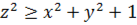 , ,  
| |
 
| |
 , ,  
| |
 , ,  
| |
 
| |
 , , 
| |
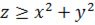 , ,  
| |

| |

| |

| |
 , ,  
| |

|
Задание 3. Вычислить с помощью поверхностного интеграла.
Найти  для части поверхности цилиндра для части поверхности цилиндра  , заключенной между плоскостями z=x, z=2x (x>0). , заключенной между плоскостями z=x, z=2x (x>0).
| |||
Найти 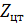 для части поверхности конуса для части поверхности конуса  , такой, что х+z £1, х,у,z ³ 0. , такой, что х+z £1, х,у,z ³ 0.
| |||
Найти площадь части поверхности цилиндра у 2=4 х, вырезанной сферой 
| |||
Найти 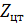 для части параболоида для части параболоида  , такой, что х+z £1, х,у ³0. , такой, что х+z £1, х,у ³0.
| |||
Найти 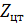 для части поверхности для части поверхности  , такой, что х+z £2, х,у,z ³ 0. , такой, что х+z £2, х,у,z ³ 0.
| |||
Найти  для части поверхности сферы для части поверхности сферы  , такой, что х£z£2х, х,у,z ³ 0. , такой, что х£z£2х, х,у,z ³ 0.
| |||
Найти 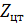 для части поверхности для части поверхности  , где , где  где z³0. где z³0.
| |||
Найти  для части параболоида для части параболоида  , такой, что х+z £2, х,у ³0. , такой, что х+z £2, х,у ³0.
| |||
Найти  для части поверхности цилиндра для части поверхности цилиндра  , заключенной между плоскостями z=х/ 2, z= 2 x (x >0). , заключенной между плоскостями z=х/ 2, z= 2 x (x >0).
| |||
Найти  для части поверхности конуса для части поверхности конуса 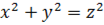 , x+y+z £1, х,у,z ³ 0. , x+y+z £1, х,у,z ³ 0.
| |||
Найти  для части поверхности конуса для части поверхности конуса  , такой, что x+z £2, х,у,z ³ 0. , такой, что x+z £2, х,у,z ³ 0.
| |||
Найти 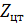 для части поверхности цилиндра для части поверхности цилиндра  , заключенной между плоскостями z=х/ 2, z= 2 x (x >0). , заключенной между плоскостями z=х/ 2, z= 2 x (x >0).
| |||
Найти  для части поверхности цилиндра для части поверхности цилиндра  x+y+z £3, х,у,z ³0. x+y+z £3, х,у,z ³0.
| |||
Найти  для части поверхности цилиндра для части поверхности цилиндра  x+y+z £3, х,у,z ³0. x+y+z £3, х,у,z ³0.
| |||
Найти  для части поверхности для части поверхности  x+z £2, х,у,z ³0. x+z £2, х,у,z ³0.
| |||
Найти  для части поверхности цилиндра для части поверхности цилиндра  x+у+z £4, у,z ³0, х ³2. x+у+z £4, у,z ³0, х ³2.
| |||
| < |
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2020-05-11 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд