Но здесь метод, изложенный Лагранжем в его книге, неожиданно, резко и полностью обрывался. Верно, что если можно решить уравнение второй степени, значит можно решить и уравнение третьей. Если мы можем решить уравнение третьей, значит можно решить и уравнение четвертой. Казалось бы, эту цепочку можно продолжить: если можно решить уравнение четвертой, значит мы в состоянии решить уравнение пятой. Как по лестнице, мы сможем подниматься выше и выше, к решению уравнений все более высоких степеней.
Можно ли восходить от одного уравнения к другому, сводить решение уравнения высшей степени к решению ближайшего уравнения низшей? Можно ли решать все алгебраические уравнения рациональными действиями и с привлечением радикалов? Другими словами, можно ли продолжить лестницу бесконечно, или она обрывается?
Галуа чувствовал, что здесь наиболее существенная задача алгебры, задача, решения которой Лагранж не знал. Метод, разработанный Лагранжем, был пригоден для уравнений вплоть до четвертой степени. Но для решения уравнения пятой степени он обращался к уравнению шестой. Таким образом, решение задачи «сводилось» к решению гораздо более сложной. Все равно что учиться прыгать с крыши Луи‑ле‑Гран, тренируясь на прыжках с башни Собора Парижской богоматери. И опять‑таки, если метод Лагранжа применять для решения уравнений шестой степени, то задача сводилась к решению уравнения десятой. Все равно что пробовать попасть на башню Собора Парижской богоматери, не взбираясь наверх, а прыгая на нее с вершины Монблана!
Сначала Галуа полагал, что должен существовать метод, доказывающий, что все алгебраические уравнения могут быть решены в радикалах. И неважно, легко ли осуществить это практически. Центральной проблемой алгебры ему казалась задача найти доказательство того, что это можно сделать, что такое решение всегда существует.
Всего через несколько недель после того, как Галуа прочитал геометрию Лежандра, он приступил к самостоятельным исследованиям.
Ему еще не было шестнадцати лет, а он уже испытал и страдание бесплодных поисков во тьме и восторг познания истины. Окружавший его мир стал призрачным. Коллеж, преподаватели, одноклассники – все это стало несущественным, почти несуществующим. Отвлеченная мысль окружила его неприступной стеной, сквозь которую не могли проникнуть ни голоса, ни события внешнего мира. Он часто забывал принести в класс нужные книги; часто сидел, уставившись на преподавателя, не слыша его вопросов, замечаний, поучений. Порой, чтобы скрыть свою обособленность, он неожиданно разражался потоком слов, которые казались непонятными или высокомерными. Он чувствовал облегчение оттого, что математика ослабила его связь с Луи‑ле‑Гран. Но ослаблена была и связь с отцом, матерью, братом и сестрой. Их образы стали расплывчатыми. Мир его мысли начал разрушать мир плоти и крови.
Ему доставляло странное удовольствие оберегать предмет своей страсти, как будто открыть его было предательством, а заговорить о нем – святотатством. Он вступил на этот путь одиноким, без друзей, без поддержки, без сочувствия. Математика казалась ему событием слишком громадным, слишком сокровенным, слишком личным, чтобы ею с кем‑то делиться. Только себе самому он с гордостью повторял: «Да, я – действительно математик».
Когда мсье Вернье впервые спрашивал Эвариста по математике, воцарилась необычная тишина. Для тех его одноклассников, кто заглядывался на странные названия книг, которые читал Эварист, наступила минута, когда ученик может смутить надоевшего учителя. Для других, кто был обижен его отрывистыми или высокомерными ответами, это была минута, когда Эвариста постигнет вполне заслуженное унижение. Молчание обескуражило и смутило доброго мсье Вернье. Эваристу было до тошноты противно на виду у всего класса отвечать на совершенно дурацкие вопросы. Первое задание мсье Вернье дал ему с самым дружеским видом.
– Покажите, как разделить угол на две равные части,
Галуа принял этот по‑детски пустяковый вопрос как оскорбление. Красный от стыда, он начертил угол, потом деревянным циркулем быстро провел дуги, расставил на чертеже буквы и, не говоря ни слова, написал:
АСЕ = ВСЕ.
– Очень хорошо.
И мсье Вернье обратился к классу:
– Многие из вас проучились в этом классе на полгода дольше Галуа, а на такой вопрос не смогли ответить и вдвое хуже.
При этих словах страдание, написанное у Эвариста на лице, обозначилось еще яснее.
– Можете ли вы объяснить, почему эти углы равны? – спросил мсье Вернье.
Он выделил слово «почему», подняв указательный палец правой руки на уровень носа. Галуа не ответил. Терпеливо и мягко мсье Вернье пояснил:
– В геометрии всегда следует доказать, почему данное положение верно. У вас всегда должен быть метод – хороший метод, который мог бы все доказать. Попробуйте объяснить, почему эти углы равны.
В мягком голосе слышалось, что мсье Вернье ничего не будет иметь против, даже если Галуа и не сумеет ответить на вопрос; ему достаточно того, что уже сделано учеником. Все будет прекрасно, если Галуа только начнет объяснять, – тут ему с радостью придет на помощь учитель.
– Почему они равны? – повторил мсье Вернье. Класс напряженно ждал, что ответит Галуа. Ответ последовал только после долгого молчания:
– Разве это не очевидно?
Весь класс разразился смехом. Кто‑то захлопал в ладоши, кто‑то крикнул:
– Для Галуа геометрия очевидна! Кто‑то другой добавил:
– Очевидно, Галуа гений!
– Тихо, тихо! – мсье Вернье старался унять класс. – Вы очень плохо ведете себя по отношению к товарищу. Ничего смешного нет. Вместо того чтобы помочь ему, вы поднимаете его на смех.
Галуа стало жаль мсье Вернье. Он добряк. Защищает ученика и не видит, бедняга, что смешки направлены и в адрес учителя.
Эварист повернулся к доске, дорисовал два треугольника, написал, что они равны, обозначил даже, почему равны, и сделал вывод о равенстве углов.
Мсье Вернье, очень довольный, смотрел на доску. – Гораздо лучше. Гораздо! Просто очень хорошо. Старайтесь работать более методично. Еще немного методичности, и вы будете одним из лучших в классе. Но помните: нужно быть внимательным и работать систематически.
Учебный год кончился. На конкурсе по математике Эварист занял второе место. Мсье Вернье был в восторге. Если бы Галуа писал более аккуратно, объяснял подробнее, он мог бы занять и первое место.
«Чуть больше методичности, еще чуть‑чуть, – думал мсье Вернье, – и через год он может принять участие даже в общем конкурсе».
Эварист занял второе место и по греческому. Узнав об этом, мсье Лабори сказал себе: «Разумеется, это доказывает, что я был прав. Второй год в том же классе пошел ему на пользу».
На другой год, в классе риторики, всего несколько месяцев спустя после того, как он впервые узнал, что означает слово «геометрия», Галуа переживал радости и муки творчества. Его дни были полны напряжения, ночи он проводил без сна. Именно ночь приносила новые идеи. Он снова и снова обдумывал их, жалея, что не может зажечь свечу и записать. Поутру он часто видел, что рассуждения его ошибочны, что ему не давал уснуть только мираж истины, которую он искал. Он занимался математикой в часы лекций, он обдумывал свои проблемы на уроках по другим дисциплинам, он работал за едой, в скудные часы досуга; он ухитрялся заниматься математикой даже в то время, когда писал сочинение по французскому языку или отвечал на вопрос преподавателя. Эти проблемы неотступно преследовали его, даже когда он читал латинские стихи или переводил с греческого. Все, чем он занимался, помимо математики, он делал машинально, не задумываясь. Под глазами у него появились темные круги, взгляд, казалось, был скорей устремлен в глубь себя, а не к внешнему миру.
Насколько же хорошо понимали своего ученика преподаватели? Вот их отзывы за первый триместр класса риторики:
«Поведение вполне сносное, – писал один. – Несколько легкомыслен. Это характер, все черты которого я и не надеюсь понять; но я вижу, что в нем преобладает самолюбие. Порочных наклонностей я у него не замечаю. Его способности кажутся мне из ряда вон выходящими как в области словесности, так и в математике. Но до сего времени он небрежно относился к классным занятиям. Вот почему он не слишком хорошо проявил себя в контрольных работах. Кажется, он решил отныне посвящать больше времени и усилий классным занятиям. Мы совместно составили для него новое расписание.
Посмотрим, сдержит ли он слово. Он кажется юношей достаточно набожным. Здоровья хорошего, но хрупок».
К этому благоприятному отзыву мсье Пьеро присовокупил свой:
«У меня работает мало. Часто разговаривает. Способности у него, следует полагать, имеются, но ни к чему хорошему они не приведут. Во всяком случае, на моих уроках он еще ни в коей мере их не обнаружил. Его занятия свидетельствуют лишь о странностях и нерадивости».
А мсье Дефорж писал:
«Всегда занят посторонними делами. С каждым Днем становится все хуже».
И, наконец, оценка доброго мсье Вернье:
«Заметное прилежание и успехи».
Год 1828
В 1823 году норвежец Нильс Генрик Абель, двадцати одного года от роду, прославился в своем родном городе тем, что, как предполагали, решил алгебраическое уравнение пятой степени. Позже Абель выяснил, что его доказательство было неверно. Как и подобает великому ученому, он настойчиво исследовал свою проблему: можно ли решить уравнение пятой степени в радикалах? Иными словами, можно ли выразить его решение конечным числом рациональных действий с коэффициентами такого уравнения и извлечением корней? Абель нашел ответ на свой вопрос. Он опубликовал его в 1826 году в первом номере «Журнала чистой и прикладной математики», издаваемого в Германии Креллем. Ответ гласил, что уравнение пятой степени обычно неразрешимо в радикалах.
Галуа на семнадцатом году жизни думал, что произвел великое открытие в математике. Он верил, что решил важную проблему и у него есть доказательство, что каждое уравнение пятой степени можно решить радикалами. Позже, вновь и вновь исследуя свое доказательство, он в минуту прозрения обнаружил, что его рассуждение неверно. То, что казалось ему открытием, достигнутым за месяцы тяжелой, упорной работы, рухнуло и превратилось в груду бессмысленных знаков. Но он не сдавался. Он знал, как это всегда знают великие ученые, что первый слабый луч света приходит только после настойчивых, непрерывных поисков; что над проблемой нужно думать дни и ночи; ждать, думать и передумывать, снова ждать, пока после непрестанных усилий первая искра понимания не выведет его на единственную узкую тропу, ведущую к решению проблемы.
После напрасных попыток решить уравнение пятой степени Галуа проникся убеждением, что такое уравнение нельзя решить в радикалах. Постепенно у него в голове стала принимать четкие очертания великая проблема алгебры: найти верные отличительные признаки, четко определяющие, можно ли при помощи радикалов справиться с данным уравнением произвольной степени. Он был уверен, что если бы такой верный критерий применить к общему уравнению пятой или другой, еще более высокой степени, такое уравнение ответило бы: «Нет, меня не решить в радикалах». Если тот же критерий применить к уравнению третьей или даже четвертой степени, ответ был бы: «Да, меня можно решить в радикалах».
Итак, ученик класса риторики Луи‑ле‑Гран Галуа определил одну из самых трудных проблем в алгебре. Однако он вряд ли мог знать, насколько важной окажется эта проблема. Он вряд ли знал, что могучие и революционные методы, которые он использует для ее решения, повлияют на развитие математики столетие спустя.
Каждый триместр профессора добросовестно записывали свои отзывы. В конце второго триместра преподаватель, наблюдавший за занятиями Галуа, писал:
«Поведение очень плохое; характер замкнутый. Оригинальничает. Способности выдающиеся, но не желает применять их в классе риторики. Для текущих занятий не делает ровным счетом ничего. Одержим страстью к математике. Я думаю, лучше бы его родители согласились, чтобы он занимался одним этим предметом. Здесь он напрасно теряет время, только мучает преподавателей и постоянно подвергается наказаниям. Не лишен религиозного чувства; здоровье, кажется, слабое».
Мсье Пьеро писал:
«Некоторые задания выполняет, а вообще болтлив, как обычно».
Мсье Дефорж:
«Рассеян, болтлив. Похоже, что задался целью меня изводить. Это могло бы послужить очень плохим примером для его одноклассников, если бы он пользовался среди них влиянием».
Мсье Вернье, учитель математики:
«Смышлен, делает заметные успехи. Недостаточно систематичен».
Эварист очень хорошо знал, за что возьмется на будущий год, когда покончит с классом риторики: он поступит в Политехническую школу.
Часто долгими ночами, усталый, Эварист гнал от себя мысли о перестановках и их произведениях, о корнях, изображенных в виде непрерывных дробей, и думал о своем недалеком будущем, рисуя себя в форме студента Политехнической школы.
Политехническая школа! Дочь революции и гордость Франции! Там ему разрешат целыми днями заниматься математикой. Больше того, он будет обязан целыми днями заниматься ею. Он встретится с людьми, которые поймут его, встретится с величайшими математиками Франции – одними из крупнейших математиков мира. Будет слушать лекции Коши. Коши признает важность проблем, которые разрабатывает он, Эварист Галуа. Он встретит Ампера и Франсуа Араго, которые пользуются любовью французского народа и восхищением учеников.
Он встретит новых товарищей, у него будут новые друзья. Правда, он ни с кем не подружился в Луи‑ле‑Гран, но в Политехнической школе у него будут друзья. Через несколько месяцев он начнет новую, настоящую жизнь в школе, где готовят не только ученых, государственных служащих и офицеров, но и народных вождей. Он знал, что для поступления в Политехническую школу нужно сдать устный экзамен. Как жаль, что устный, а не письменный! Он должен выдержать! Придется открыть экзаменатору свои познания, может быть и вопросы, над которыми он работает, и результаты, которых удалось добиться. Эта мысль была неприятна, даже мучительна.
Он вспоминал свой последний разговор с отцом. Он открыл отцу свою любовь к математике, свои планы поступления в Политехническую школу. Отец его понял. Всегда отец, никто другой. Преподаватель математики учит его уже больше года и ни разу не заподозрил, как многое он мог бы получить у собственного ученика.
Но отец понял. Гордостью загорелись его глаза, когда он весело сказал:
– Мой сын будет великим математиком. Эварист Галуа, профессор Политехнической школы, член академии. Да, Эварист, это звучит хорошо. Мне нравится.
И он рассмеялся. Но смех его был недолгим и чуть принужденным. Не то что в прежние времена. Глаза отца быстро затуманились, когда он произнес:
– Надеюсь, ты не встретишь в жизни столько врагов, как я. – Остальное он сказал очень тихо, как бы про себя. Эварист еле смог расслышать его: – Это еще не самое страшное. Хуже всего равнодушие. – Он живо повернулся к сыну. – Ну вот, я тебе порчу все удовольствие. Мсье Вернье пишет мне, что у тебя очень хорошо идут дела с математикой. Не похоже, что он так глуп, как ты изображаешь. Он советует тебе остаться в Луи‑ле‑Гран еще на год и специализироваться по математике. Так поступают все, кто собирается идти в Политехническую школу. Что ты думаешь на этот счет?
Эварист был зол на мсье Вернье. С какой стати он вмешивается в его дела? Какое разочарование: отец готов еще на год оставить его в Луи‑ле‑Гран!
Он сам удивился, как холодно прозвучал его голос:
– И ты не веришь, что я знаю достаточно, чтобы сдать этот дурацкий экзамен?
– Мсье Вернье пишет, что ты, пожалуй, знаешь слишком много, чтобы выдержать. Ты знаешь сущность, но можешь не знать маловажных деталей, которые постоянно спрашивают экзаменаторы. Он решительно советует, чтобы ты остался в Луи‑ле‑Гран ещё на год.
– Мсье Вернье стар и глуп.
Теперь он жалел, что сказал эти слова.
Год 1828
Был час, когда ученики Луи‑ле‑Гран писали письма родителям, друзьям и родственникам. В Луи‑ле‑Гран все подчинялось жесткому расписанию, даже сыновняя любовь.
Эварист писал:
«Дорогой отец! Неделю тому назад я послал тебе отчаянное письмо, которое должно было огорчить тебя. Но твой невозмутимый и добрый ответ мне очень помог. Я теперь чувствую себя не таким несчастным и более спокойным. Что это была за тягостная неделя! Когда я не выдержал вступительного экзамена, меня оставила всякая надежда, сама жизнь стала мне не мила. Потом я стал повторять себе твои слова. Как ты добр, говоря, что ты не потому обеспокоен, что не веришь в меня, но именно потому, что веришь!
Теперь мне понятно, что ты допускал мысль о неудачном исходе, когда советовал мне остаться еще на год в Луи‑ле‑Гран и специализироваться по математике. И вот я в Луи‑ле‑Гран еще на целый год! По‑видимому, такова моя судьба – проводить жизнь в этом здании, этой тюрьме, которую я знаю так хорошо и так ненавижу. Я не подозревал, что могу столь сильно презирать человека, к которому лишь несколько месяцев тому назад относился с почтением. Я говорю о моем экзаменаторе мсье Лефевре. Это посредственный ученый, лицо которого похоже на череп, обтянутый морщинистой желтой кожей. С первого же взгляда он показался мне крайне отталкивающим и бесчеловечным существом. Этот экзаменатор школы, о которой я мечтаю, сиплым голосом задавал мне свои нелепые вопросы. По его голосу и выражению его лица я чувствовал, что ученик для него – мусор под ногами. Я уверен, что он иезуит.
Единственное, что нужно было от нас этому желтому черепу, это чтобы мы протараторили ему формулы, не понимая их. Он хотел, чтобы объяснения ему давали как в плохом учебнике. Думать и рассуждать необычно – это он считает преступлением.
Когда очередь дошла до меня, он посмотрел на меня своими крохотными глазками и еще прикрыл их слегка, чтобы видеть меня как можно меньше. Затем он задал первый вопрос:
– Почему вы явились сюда, не пройдя специального курса математики?
Я ответил:
– Я занимался самостоятельно.
– Ах, так!
Слышал бы ты это «Ах, так!». Потом он спросил меня, как решить уравнение второй степени. Он посмел задать этот оскорбительный вопрос мне, знающему об алгебраических уравнениях больше, чем все профессора Политехнической школы, вместе взятые. А кроме того, его вопрос был неправильно сформулирован. Когда я сказал, что вопрос не так поставлен, желтый череп скривился в насмешливой улыбке. Он уклонился от моего замечания, заявив, что ему некогда заниматься спорами и что экзаменуюсь я, а не он. Он задал мне затем самые детские вопросы. Я почувствовал, как у меня сжалось горло; я не мог издать ни звука. Тогда череп повернулся ко мне:
– Вижу, что вы занимались самостоятельно. Но вы недостаточно занимались. Вам будет лучше прийти снова в будущем году.
Дорогой отец! Я послушаюсь тебя и постараюсь выучить эти пустяки, чтобы в будущем году отвечать тем языком, который им хочется услышать. Надеюсь, что тогда добьюсь большего успеха.
Теперь оставим эту неприятную тему.
Милый отец! Когда я видел тебя в последний раз, ты казался подавленным. Спасибо, что ты рассказал мне кое‑что о твоих огорчениях. Твои слова только подтвердили мои подозрения. Но людям, затеявшим против тебя подлейшую и омерзительнейшую кампанию клеветы, не добиться успеха! Им никогда не запятнать твоего честного имени! Жители Бур‑ля‑Рен знают своего славного мэра и не станут слушать клевету, которую распространяет приходский священник. Иезуиты, возможно, сильны, но не настолько, чтобы отвратить от тебя тех, кто тебя любит».
Галуа остановился и перечитал последние слова. Они звучали не так, как следовало. Они не принесут отцу облегчения, в котором тот нуждается. Эварист написал:
«Мой дорогой отец! Как я хотел бы помочь тебе моей любовью! Отплатить тебе за привязанность, дружбу, понимание! Вместо этого я только усугубляю твое горе рассказами о собственных несчастьях. Но, подобно тебе, я верю, что настанут другие времена. Придет буря, которая очистит воздух в Париже, в Бур‑ля‑Рен, во всей Франции. Будем надеяться, что это произойдет скоро».
Зазвонил колокол. Пора было кончать письмо. Эварист быстро дописал:
«Пожалуйста, постарайся как можно лучше объяснить мою неудачу матери. Обнимаю тебя и всех вас.
Эварист».
Затем он отправился в небольшую комнату специального класса математики и там вместе с двадцатью другими учениками стал ждать начала первой лекции нового профессора.
Мсье Ришар вошел в класс без каких‑либо драматических эффектов. Закрыв за собой дверь, он туманно улыбнулся и помедлил как бы в нерешительности. Потом подошел к кафедре, повернулся к ученикам широкой, слегка сутулой спиной, взял кусок мела, переломил пополам и встал к классу лицом. Рассеянным взглядом осмотрел учеников. Класс внимательно изучал рослого профессора, его квадратную голову с редеющими волосами, с дружелюбным прищуренным взглядом за толстыми стеклами очков. Заговорил он очень спокойно, не прибегая к ораторским приемам. Кое‑кому из слушателей показалось странным, что этот человек, разговаривающий так себе, запросто, как будто дома с друзьями, пользуется славой лучшего преподавателя Луи‑ле‑Гран. Все, однако, слушали его.
– Целью этого курса, мои молодые друзья, будет расширить ваши познания в математике. Мы постараемся не только расширить, но и углубить их. Попробуем достигнуть этого, начав еще раз все сначала. Мы быстро повторим известный вам материал, но уже с более передовой, более современной точки зрения. Этот быстрый обзор позволит нам увидеть главные, наиболее существенные теоремы, лежащие в основе всех прочих. В математике особенно велика опасность не заметить леса за деревьями, увидеть мелкие теоремы и забыть структуру целого, в котором появляются эти теоремы и которое связывает их воедино.
Час, когда мсье Ришар будет читать лекцию, Эварист готовился посвятить своей собственной работе. Но теперь он прислушался.
– Посвятим наше внимание геометрии. Когда вы узнали о ней впервые, у вас, вероятно, осталось такое впечатление, что геометрия в окончательном и завершенном виде появилась на свет внезапно, порожденная мыслью одного человека, и, может быть, даже сразу в виде книги. Однако, подобно любой другой отрасли математики, геометрия – результат работы целых поколений. Ее главным образом связывают с именем Эвклида, который жил приблизительное третьем веке до рождества Христова. Но геометрия началась задолго до Эвклида. Быть может, вы спросите меня: «Когда она была закончена?» Она не кончена и по сей день и, как я полагаю, не завершится никогда.
И мсье Ришар обрисовал историю геометрии. Он говорил о том, что ей дали начало египтяне как практической науке об измерениях, и о том, какую роль сыграли в ее развитии греки.
Все это было ново для Галуа. Ему не хотелось сознаться, что для понимания математики важно знать ее историю. И все‑таки пришлось признать, что все сказанное мсье Ришаром интересно, что манера изложения ему нравится. И – это был величайший комплимент, который мог сделать Галуа, – он слушал.
– Весьма опасно, когда результатом преподавания является впечатление, что математика подобна закрытой книге, подобна достроенному зданию, полученному нами от минувших веков; зданию, к которому нечего прибавить, в котором ничего нельзя изменить. Математика – живой организм. А в наше время, в девятнадцатом веке, она живет особенно бурно. Даже элементарная геометрия может явиться источником новых, очень важных открытий. Друзья мои, вы можете подумать, что сомнения и творчество приходят только после того, как вполне овладеешь предметом. Вы можете подумать, что только когда вы усвоили все познания в данной области математики, лишь тогда, пожалуй, у вас могут возникнуть собственные мысли. Это, может быть, как правило, и верно, но не обязательно. И опять‑таки геометрия представляет собой в этом смысле хороший пример. Тут мы видим, что сомнения и трудности появляются у нас с самого начала. Это станет понятнее, если мы в нескольких словах рассмотрим историю эвклидовых постулатов, или, как мы их сегодня называем, аксиом.
Мсье Ришар перечислил пять постулатов Эвклида и один за другим разобрал их, пока не дошел до пятой аксиомы.
– История пятой аксиомы прямым путем ведет нас в современность. Эта аксиома никогда не казалась столь же очевидной, как четыре другие. Делались многочисленные попытки заменить ее другой, более очевидной. Можно ли доказать пятую аксиому, или следует ее допустить? Каким образом сделать и то и другое? Вопрос остается нерешенным, и будущее может принести вам новые и неожиданные открытия.
Эварист подумал, как не похожи мсье Ришар и мсье Вернье. Пришлось признаться, скрепя сердце, что у нового профессора можно, пожалуй, даже научиться кое‑чему.
«Сам мсье Ришар, – думал Галуа, – не крупный математик. Но математика ему нравится, и он с любовью и пониманием постиг ее сущность. Даже если он по‑настоящему и не занимался творческой работой, он видит, как она прекрасна, и знает, как заставить других увидеть ее красоту». Эварист решил, что мсье Ришар – человек, с которым стоит познакомиться. Такому он, Эварист Галуа, мог бы даже открыть свои способности.
Мсье Ришар диктовал задачи на неделю. Большинство учеников считало их трудными, требующими многих часов работы. Даже хорошим ученикам решить все удавалось редко.
Студенты переписывали в тетради: «Задача I. Найти две диагонали х и у четырехугольника, вписанного в окружность, выразив их через его четыре стороны а, b, с, d». Потом записали вторую и третью задачи. Эварист только слушал. Когда диктовка закончилась, у него перед глазами стояло четкое решение каждой задачи. Мсье Ришар приступил к чтению лекции.
Эварист вырвал лист из тетради, написал наверху «Галуа», пониже – «Задачи». Сформулировал первую и написал ее решение, пользуясь уравнениями и связывая их воедино сжатыми пояснениями. Не перечеркнув и не исправив ни единого слова, он самым простым путем достиг искомого ответа и подробно записал, чему равняются xy и 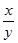
. Потом на другой странице так же тщательно написал точное решение оставшихся двух задач, снабдив каждое аккуратным чертежом. На все это у него ушло пятнадцать минут, после чего он не столько слушал лекцию мсье Ришара, сколько набирался храбрости, готовясь к концу урока.
Выходя из класса, мсье Ришар услышал:
– Простите, мсье Ришар.
– Да?
Преподаватель увидел худого и невысокого для своего возраста ученика с залитым краской треугольным лицом. Ученик глядел в пол и протягивал преподавателю лист бумаги.
Мсье Ришар положил Эваристу руку на плечо.
– Что случилось?
Не поднимая головы, Эварист отдал листок мсье Ришару.
– Вот решение.
Мсье Ришар взглянул на первую страницу, быстро прочел ее; такое решение сделало бы честь лучшему учебнику. Он перевернул страницу, посмотрел на нее, перевел взгляд на ученика, потом снова на бумагу и опять на Галуа. Вернулся к первой странице и прочел вслух:
– «Галуа»: Как вас зовут?
– Эварист.
– Так.
Долго и не говоря ни слова мсье Ришар смотрел на юношу. Эваристу было стыдно, он пожалел о своем поступке. Неужели он выставил себя на смех? Неужели мсье Ришар сейчас иронически улыбнется, как тот желтый череп?
– Не зайдете ли ко мне сегодня после обеда? – сказал мсье Ришар. – Можно будет побеседовать подольше. Я попрошу надзирателя не казнить вас лютой казнью, если вы вернетесь в спальню чуть позже. Решено?
– Да, мсье.
– Хорошо.
Галуа весь пылал от возбуждения. Уходя, он услышал, как один из учеников свистнул и сказал соседу:
– Подумать только! Наш гений пробует заводить друзей.
Слышал он и ответ соседа:
– Боюсь, что это его прикончит.
Как большинство профессоров, мсье Ришар жил в Луи‑ле‑Гран. Когда Эварист вошел, мсье Ришар указал ему на стул напротив себя, с минуту смотрел на него молча. Затем сказал, набивая трубку:
– Мне хотелось бы, чтобы вы что‑нибудь рассказали о себе. Над чем вы сейчас работаете?
Секрет успеха, которым мсье Ришар пользовался среди студентов, был очень прост. То был результат одного принципа, которым руководствовался профессор: обращаться с учениками как с равными.
Эварист был поражен: ему не пришлось убеждать мсье Ришара, что он математик. Каким‑то странным образом мсье Ришар, по‑видимому, это знал. Впервые за время своего пребывания в Луи‑ле‑Гран Эварист ощутил робость и смирение.
– Работаю над алгебраическими уравнениями. Год назад я думал, что уравнение пятой степени можно разрешить радикалами, подобно уравнениям третьей и четвертой степени. Теперь я полагаю, что общее уравнение пятой степени неразрешимо в радикалах.
Галуа замолчал. Мсье Ришар в изумлении глядел на сидящего напротив него ученика, но вслух сказал только:
– Хм! Интересно. Очень интересно!
– Проблема, которую я сейчас разрабатываю, является, в сущности, гораздо более общей. Я ищу условия, необходимые и достаточные для того, чтобы алгебраическое уравнение можно было решить в радикалах. Я имею в виду алгебраические уравнения произвольной степени. Я верю, я даже убежден, что такой критерий существует. Я полагаю, мсье, – добавил он доверительно, – что за последнее время я добился некоторых успехов в решении этой проблемы.