Стратегия первого (второго) игрока есть функция
которая каждой области информированности 
ставит в соответствие число
являющееся номером одного из принадлежащих ей ребер альтернатив.
Т.О., стратегией игрока является система правил, однозначно определяющих выбор игроком личного хода (ребра-альтернативы) во всех возможных позициях игр, которые могут встретиться в любой партии игры.
Обозначим 
– стратегии с номером i и j первого и второго игрока соответственно.
Принятие обоими игроками определенной стратегии однозначно определяет в игре без случайных ходов реализацию игры в виде пути по графу от начальной позиции игры А до одной из конечных позиций игры 
, а значит и выигрыши обоих игроков 
При наличии случайных ходов в игре реализация игры, а значит, и выигрыши игроков оказываются случайными.
Зная вероятностное распределение 
на множестве конечных позиций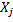 
(j=1,2,…,N) графа, соответствующее стратегиям 
игроков, можно найти математическое ожидание случайных выигрышей обоих игроков
Заметим, что понимание выигрышей игроков как среднего значения случайного выигрыша, допускает в качестве личного хода игрока случайный ход. При этом игрок, делающий очередной ход сам может задать на множестве альтернатив своего хода желаемое ему вероятностное распределение и предоставить ход генератору случайных числе, который будет реализовывать заданное распределение при многократных повторениях партий игры.
Иногда таким неожиданным выбором хода можно повлиять на рост математического ожидания своего выигрыша более существенно (при многократном повторении партий игры), чем постоянным выбором какой-либо определенной альтернативы. Такие стратегии называются смешанными стратегиями.
|
|
В отличие от смешанных стратегий игроков чистые стратегии соответствуют выбору во всех позициях определенных альтернатив.
Для иллюстрации целесообразности смешанных стратегий игроков при многократном повторении партий игры, рассмотрим игру в «орлянку»
Игрок 1 выбирает цифру или герб; игрок 2, не зная выбора 1 игрока, также выбирает цифру или герб.
Если оба совершают одинаковый выбор, то игрок 2 выигрывает единицу у 1го, иначе игрок 1 выигрывает единицу у 2-го.
Граф – дерево игры имеет вид (найдите ошибку):
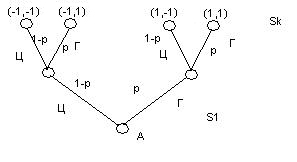
В качестве наиболее разумного решения для обоих игроков оказываются случайные личные ходы с гистограммой вероятностного распределения по альтернативам (1/2,1/2). Действительно, пусть второй игрок заметил, что частота выбора герба первым игроком равна 
, тогда, выбирая для себя герб также с частотой p, средний выигрыш второго игрока оказался бы равным:
Если же p=1/2, то 
Выбор игроками своих определенных стратегий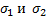 
называют ситуацией игры.
Каждой ситуации игры 
соответствует определенное значение выигрышей игроков
и 
Поэтому результаты игры можно описать в виде двух матриц, определяющих выигрыши игроков в зависимости от ситуации игры в чистых стратегиях. Эти матрицы называются платежными матрицами конечной игры.
| 
| 
| … | 
|
| 
| 
| … | 
|
| 
| 
| … | 
|
| … | … | … | … | … |
| 
| 
| … |
|
|
|
|
| … |
|
|
| 
| 
| … | 
|
|
| 
| 
| … | 
|
| … | … | … | … | … |
|
| 
| 
| … |
|
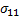
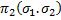
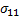
С точки зрения обоснования выбора стратегии игроков и оценки ожидаемых результатов игры информация, содержащаяся в платёжных матрицах, является эквивалентной описанным вышей строгим правилам игры, поэтому задание платежных матриц называют заданием игры с помощью платёжных матриц.