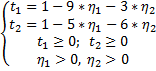К общим методам решения антагонистических игр относятся приближенный итеративный метод и точный метод решения посредством сведения решения игры к решению основной задачи линейного программирования (ОЗЛП).
Итеративный метод решения или метод фиктивного разыгрывания состоит в проигрывании серии партий со строго формализованными правилами выбора ими решений каждой партии.
Правила выбора первым игроком своей чистой стратегии в (N+1)-й партии, если в предыдущих N-партиях второй игрок использовал свою стратегию 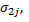 j=1,2,…,n ровно
j=1,2,…,n ровно  раз (
раз (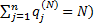 основывается на двух идеях:
основывается на двух идеях:
1) первый игрок допускает, что частоты  применения вторым игроком своих чистых стратегий
применения вторым игроком своих чистых стратегий  , имевшие место в предыдущих N-партиях, сохраняется и в (N+1) партии.
, имевшие место в предыдущих N-партиях, сохраняется и в (N+1) партии.
В результате такого прогноза первый игрок ставит себя в условие полной информации о применяемой противником смешанной стратегии игры;
2) в этих условиях первый игрок выбирает в (N+1)-ой партии свою чистую стратегию 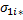 , оптимизирующую его ответ на известную смешанную стратегию противника, т.е. реализующую экстремум в правой части выражения
, оптимизирующую его ответ на известную смешанную стратегию противника, т.е. реализующую экстремум в правой части выражения

Формализованное правило выбора вторым игроком своего решения в (N+1)-ой партии игры базируется на тех же идеях:
второй игрок выбирает в (N+1)-ой партии стратегию  , реализующую экстремум в правой части выражения:
, реализующую экстремум в правой части выражения:

В первой партии игры стратегии 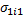 и
и  выбираются произвольно, т.е. для N=1
выбираются произвольно, т.е. для N=1
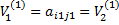
Оказывается, при т.о. организованном разыгрывании серии партий игры, имеет место теорема:
Теорема (Брауна и Робинсона). При неограниченно продолжающемся фиктивном разыгрывании серии партий по изложенным выше правилам справедливо утверждение:
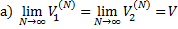
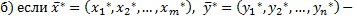
- векторы одной из (любой) оптимальных. стратегии первого и второго игрока в игре с платежной матрицей А, то число 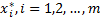 содержится среди предельных точек числовой последовательности
содержится среди предельных точек числовой последовательности 
а число  содержится среди предельных точек последовательности
содержится среди предельных точек последовательности 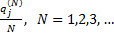
В частности, если ситуация равновесия (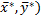 в данной игре единственная, то
в данной игре единственная, то

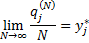
Организацию фиктивного разыгрывания серии партий игры и теорему Брауна и Робинсона можно использовать для приближенного итеративного решения произвольной антагонистической игры, заданной в матричной форме.
Характерной особенностью метода является его медленная сходимость и большое необходимое количество итерация для обеспечения заданной точности решения.
Пример: Решить игру методом итераций
1) первая партий игры
N=1; i*=2; j*=2; 
Включается счетчик партии
 =0;
=0; 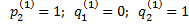
2) вторая партия игры:
N=2; 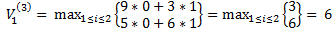 , i*=2
, i*=2
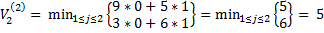 , j*=1
, j*=1

 = 0;
= 0; 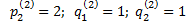
3) третья партия игры
N=3; 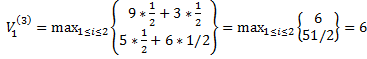 , i*=1
, i*=1
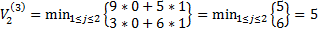 , j*=1
, j*=1

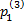 =1;
=1; 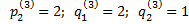
4) четвертая партия игры:
N=4; 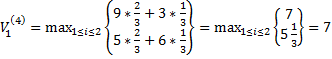 , i*=1
, i*=1
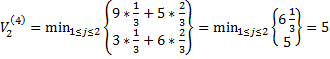 , j*=2
, j*=2

 =2;
=2; 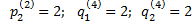
и т.д.
N=15
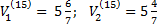
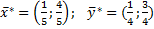
Точное решение:


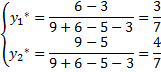
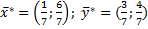
Признаком окончания процесса разыгрывания используется следующее:
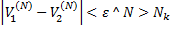
где  – минимальное допустимое количество партий разыгрывания
– минимальное допустимое количество партий разыгрывания
Обсудим общий точный метод решения антагонистических игр сведением решения игры к решению основной задачи линейного программирования (ОЗЛП).
Из свойства ситуации равновесия в игре для оптимальной стратегии игрока имеем следующее неравенство:

Не нарушая общности можно считать V > 0 (этого всегда можно добиться, прибавляя ко всем элементам матрицы А одну и ту же достаточно большую положительную величину М – при этом цена игры увеличится на М, а решение игры – не изменится).
Итак, получаем:
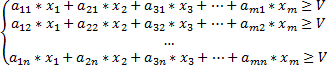
Разделим все неравенства на V > 0 и введем новые переменные:

Тогда получим:
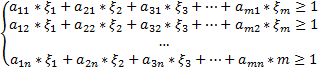
Причем: 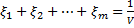
Первый игрок стремится сделать свой гарантированный выигрыш максимальным, тогда правая часть последнего равенства принимает минимальное значение.
Т.О. задача решения игры свелась к следующему:
Определить неотрицательные значения переменных 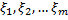 так, чтобы они удовлетворяли линейным ограничениям и при этом их линейная функция
так, чтобы они удовлетворяли линейным ограничениям и при этом их линейная функция  обращалась в минимум.
обращалась в минимум.
Это типичная задача линейного программирования, решая которую мы найдем оптимальную стратегию 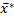 первого игрока. Задача легко сводится к ОЗЛП.
первого игрока. Задача легко сводится к ОЗЛП.
Действительно, введем в рассмотрение n – новых переменных.
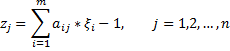
Тогда, очевидно,  и получаем ОЗЛП вида:
и получаем ОЗЛП вида:
Определение оптимального для первого игрока вектора  сводится к поиску минимума
сводится к поиску минимума 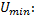

при наличии ограничений:
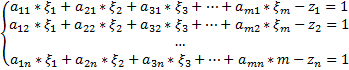


Пусть полученная ОЗЛП решена, и ее решением является вектор
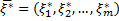

и минимальное значение линейной формы 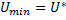
Тогда оптимальной стратегией первого игрока будет вектор с компонентами:
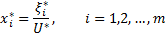
а цена игры V = 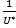
Для второго игрока все будет аналогично с той разницей, что второй игрок будет максимизировать величину W = 1/V, а ограничения на переменные будут иметь вид:
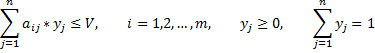
После деления обеих частей на V и ввода новых переменных:


Получим ОЗЛП для второго игрока:
Определить вектор 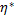 , максимизирующий линейную формулу:
, максимизирующий линейную формулу:
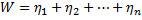
при ограничениях:
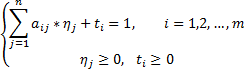
После решения ОЗЛП находим 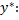
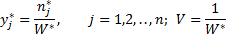
Обе оптимизационные задачи линейного программирования, полученные для первого и второго игрока в теории линейного программирования называются сопряженными (двойственными) друг другу.
Равенство 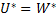 для сопряженных друг с другом ОЗЛП является одним из основных результатов в теории линейного программировании, эквивалентным основной теореме игр – теореме Неймана
для сопряженных друг с другом ОЗЛП является одним из основных результатов в теории линейного программировании, эквивалентным основной теореме игр – теореме Неймана
Пример: свести решение игры к решению ОЗЛП
| 9 | 3 |
| 5 | 6 |
Для первого игрока:
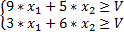
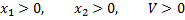
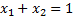
Обозначим 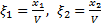

Тогда получим:
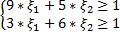

Введем новые переменные:
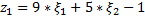
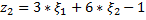
и получаем ОЗЛП вида:
найти min U=min( 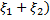 при ограничениях
при ограничениях
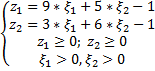
Для второго игрока:


Обозначим:

W = 
Тогда получаем:
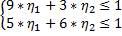
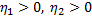
Введем новые переменные:
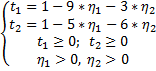
Получаем ОЗЛП вида:
Найти max W = max(  при наличии ограничений:
при наличии ограничений: