Пусть T – случайная величина, равная времени, прошедшему между произвольными моментами поступления двух соседних событий в простейшем потоке.
Найдем ее функцию распределения: F(t)=P(T<t);
Перейдем к вероятности противоположного события:
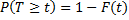
это есть вероятность того, что на участке времени длиной t от момента появления одного из событий не появится ни одного из следующих событий, т.е.

| F(t) |
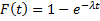 – интегральный закон распределения между двумя событиями потока.
– интегральный закон распределения между двумя событиями потока.
| t |
Дифференцируя, находим плотность распределения:
| f(t) |
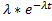
| t |
- показательный закон распределения.
Закон распределения СВ с такой плотностью называется показательным законом.
Математическое ожидание СВ T:
M[T]= 


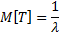
Дисперсия СВ T
D[T]= 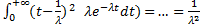
D[T]= 
Докажем важное свойство показательного закона:
| T |
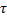 , то это никак не влияет на закон распределения величины оставшейся части промежутка (T-
, то это никак не влияет на закон распределения величины оставшейся части промежутка (T-  – он будет таким же, как и закон распределения всего промежутка T, т.е. показательным.
– он будет таким же, как и закон распределения всего промежутка T, т.е. показательным.

|
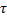
|
T- 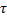
|
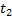
|
| t |
Предположим, что от начала случайного промежутка времени T с функцией распределения:
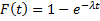
уже прошло некоторое время 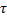 , т.е. произошло событие
, т.е. произошло событие 
Найдем закон распределения величины оставшейся части промежутка 
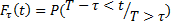
Докажем, что условный закон распределения 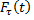 не зависит от
не зависит от 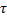 и равен F(t), т.е.
и равен F(t), т.е.

По теореме умножения вероятностей:
вероятность произведения двух событий: P(A*B)=P(A)*P(B)


Событие 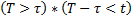 равносильно событию
равносильно событию  , т.е.
, т.е.
 (
(
Кроме того:
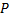 (T>
(T> 
Тогда получаем

т.е. 
Можно доказать, что показательный закон единственный, обладающий таким свойством, являющимся следствием одного из основных свойств простейшего потока – отсутствие последействия.
Дополнительные сведения о потоках событий:
1) нестационарный пуассоновский поток
Отсутствуют условия стационарности. Основная характеристика – мгновенная плотность λ(t):
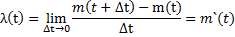
где m(t) – математическое ожидание числа событий на участке (0, t)
Для такого потока случайное число событий, попадающих на участок длины 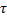 , с началом в т.
, с началом в т.  распределено по закону Пуассона.
распределено по закону Пуассона.
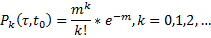
где m - математическое ожидание числа событий на участке (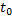 ,
, 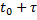 )
)
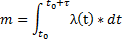
Закон распределения промежутка T между событиями зависит от момента поступления первого события  и вида функции
и вида функции 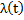 и уже не является показательным.
и уже не является показательным.


2) поток с ограниченным последействием
ОПР. Ординарный поток однородных событий называется потоком с ограниченным последействием (или потоком Пальма), если промежутки времени между последовательными событиями  представляет собой независимые одинаково распределённые СВ (независимость интервалов
представляет собой независимые одинаково распределённые СВ (независимость интервалов  не является достаточным условием для отсутствия последействия).
не является достаточным условием для отсутствия последействия).
Важным для практики примером потоков Пальма является так называемые потоки Эрланга.
ОПР. Потоком Эрланга k-ого порядка ( называют поток, получаемый из простейшего, если сохранить каждое (k+1) событие, а остальные k промежуточных событий выбросить.
называют поток, получаемый из простейшего, если сохранить каждое (k+1) событие, а остальные k промежуточных событий выбросить.
Например:

|
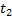
|

|

|
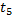
|
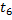
|
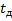
|

|

|

|
Можно показать, что закон распределения величины промежутка времени T между соседними событиями потока Эрланга k-ого порядка и его характеристики имеют вид:
-плотность распределения;



где  – плотность порождающего простейшего потока, который подвергался «прореживанию».
– плотность порождающего простейшего потока, который подвергался «прореживанию».
Выражения для характеристик через плотность  самого потока
самого потока 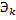 :
:

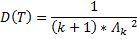
где 
Если  сохраняет константы, то при
сохраняет константы, то при  поток Эрланга заданной плотности
поток Эрланга заданной плотности  неограниченно приближается к регулярному потоку с постоянным интервалом между событиями
неограниченно приближается к регулярному потоку с постоянным интервалом между событиями
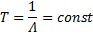
т.к. D(T) 
Т.О., задаваясь различными K, получаем потоки, обладающие различным последействием – от полного его отсутствия при k=0 до жесткой связи между моментами появления событий при  , т.е. порядок потока Эрланга
, т.е. порядок потока Эрланга  определяет «меру последействия», имеющегося в потоке. Этот факт используется на практике: реальный поток событий, имеющий последействие, заменяет потоком Эрланга с тем же последействием.
определяет «меру последействия», имеющегося в потоке. Этот факт используется на практике: реальный поток событий, имеющий последействие, заменяет потоком Эрланга с тем же последействием.
3) неординарные потоки
В таких потоках события поступают не по одиночке, а группами (парами, тройками и т.д.), причем свести поток к ординарному (объединением событий в поток пар, троек и т.д.) не удается, т.к. каждое событие случайным образом может оказаться двойным, тройным и т.д.
Лекция 4. Пуассоновские потоки событий и непрерывные марковские цепи.
Пусть система X в момент t находится в состоянии 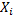 и может перейти из него в состояние
и может перейти из него в состояние 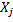 под влиянием какого-нибудь пуассоновского потока событий с интенсивностью
под влиянием какого-нибудь пуассоновского потока событий с интенсивностью  : как только появляется первое событие этого потока система мгновенно переходит из
: как только появляется первое событие этого потока система мгновенно переходит из 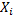 в
в 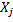 .
.
Вероятность появления ровно одного события за время 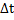 равна:
равна:
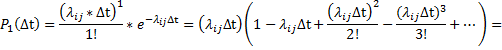

Но с другой стороны вероятность перехода  из
из 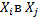 за время
за время 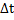 равно:
равно:

Однако заключаем, что плотность вероятности перехода  в непрерывной цепи Маркова представляет собой не что иное, как интенсивность потока событий, переводящего систему по соответствующей стрелке.
в непрерывной цепи Маркова представляет собой не что иное, как интенсивность потока событий, переводящего систему по соответствующей стрелке.
Если все потоки событий, переводящие сист. X из состояния в состояние пуассоновские (простейшие), то процесс, протекающий в системе будет марковским.
Действительно, пуассоновский поток обладает свойством отсутствия последействия, поэтому при заданном состоянии системы в данный момент ее переходы в другие состояния в будущем обусловлены только появлением каких-то событий в пуассоновских потоках, а вероятность появления этих событий не зависит от предыстории процесса.
Итак, рассматривается система X, в кот. переходы из состояние в состояние происходят под действием пуассоновских (простейших) потоков событий с определенными интенсивностями. Проставим эти интенсивности (они же – плотности вероятности переходов) на графе состояний у соотв. стрелок. Получим размеченный граф состояний, по кот. записываем систему ДУ Колмогорова для вероятностей состояний.
Пример. Группа в составе 5 самолетов в строю «колонна» совершает налет на территорию противника. Передний (ведущий) самолет является постановщиком помех. До тех пор, пока он не сбит, идущие за ним самолеты не могут быть окружены и атакованы средствами ПВО. Атакам подвергается только постановщик помех. Поток атак – пуассоновский (простейший) с интенсивностью  . В результате одной атаки ведущий поражается с вероятностью p. Если он сбит, то следующий за ним самолеты обнаруживаются и подвергаются атакам ПВО. На каждый из них (до тех пор, пока он не поражён) направляется пуассоновский поток атак с интенсивностью
. В результате одной атаки ведущий поражается с вероятностью p. Если он сбит, то следующий за ним самолеты обнаруживаются и подвергаются атакам ПВО. На каждый из них (до тех пор, пока он не поражён) направляется пуассоновский поток атак с интенсивностью  , каждой атакой самолет поражается с вероятностью p. Когда самолет поражен, атаки на него прекращаются, но на другие самолеты не переносятся.
, каждой атакой самолет поражается с вероятностью p. Когда самолет поражен, атаки на него прекращаются, но на другие самолеты не переносятся.
Написать уравнения Колмогорова для вероятностей состояний и указать начальные условия.
Возможные состояния системы.
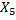 – все самолеты целы;
– все самолеты целы;
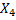 - постановщик помех (ведущий) сбит, остальные целы;
- постановщик помех (ведущий) сбит, остальные целы;
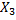 - ведущий и один самолет сбиты, а остальные целы;
- ведущий и один самолет сбиты, а остальные целы;
 – ведущий и два самолета сбиты, а остальные целы;
– ведущий и два самолета сбиты, а остальные целы;
 - ведущий и три самолета сбиты, а один цел;
- ведущий и три самолета сбиты, а один цел;
 – все самолеты сбиты.
– все самолеты сбиты.
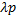
|
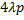
|

|

|
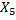
|
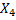
|
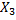
|

|

|

|
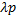
|
Из 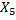 в
в 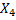 систему переводит поток поражающих атак интенсивности
систему переводит поток поражающих атак интенсивности 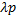 (интенсивность потока атак
(интенсивность потока атак  , но не все они поражающие, каждая из них оказывается поражающей только с вероятностью p).
, но не все они поражающие, каждая из них оказывается поражающей только с вероятностью p).
Найдем 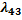 . Система находится в
. Система находится в 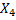 и могут быть атакованы 4 самолета. Она перейдет в
и могут быть атакованы 4 самолета. Она перейдет в 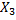 время
время 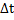 , если за это время будет сбит один самолет (все равно какой).
, если за это время будет сбит один самолет (все равно какой).
Один самолет сбивается с вероятностью  , тогда один самолет из 4х сбивается с вероятностью:
, тогда один самолет из 4х сбивается с вероятностью:
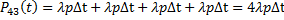
(вероятность суммы несовместных событий)
Откуда 
Аналогично получаем:

Уравнения Колмогорова для вероятностей состояний имеет вид:

Т.к. в начальный момент все самолеты целы, то

Предельные вероятности состояний.
Интегрирование системы уравнений Колмогорова в аналитическом виде при n>2 представляет значительные трудности. Ситуация упрощается, если существует установившееся решения этой системы, т.е. если функции  стремятся к каким-то пределам при
стремятся к каким-то пределам при  , т.е. графики функции имеют горизонтальные асимптоты.
, т.е. графики функции имеют горизонтальные асимптоты.

|

|

|

|

|

|
Эти пределы 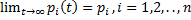 , если они существуют, называются предельными (или «финальными») вероятностями состояний.
, если они существуют, называются предельными (или «финальными») вероятностями состояний.
Это означает, что с течением времени в системе X устанавливается предельный стационарный режим, в ходе кот. она переходит из состояния в состояние, но вероятности состояний уже не меняются во времени. В этом предельном режиме каждая предельная вероятность может быть истолкована как среднее относительное время пребывания системы в данном состоянии!!!
ОПР. Система, для которой существует предельная вероятность, называется эргодической и соответствующий СП – эргодическим.
Если существует предельный стационарный режим и предельные вероятности состояний, то переходя к пределу в системе Колмогорова при  , получаем алгебраическую систему уравнений, т.к. левые части уравнений равны нулю, решая кот. находим значения предельных вероятностей
, получаем алгебраическую систему уравнений, т.к. левые части уравнений равны нулю, решая кот. находим значения предельных вероятностей  , представляющих наибольший интерес.
, представляющих наибольший интерес.
В каких случаях система является эргодической?
Если система X имеет конечное число состояний  , то для существования предельных вероятностей достаточно, чтобы из любого состояния системы можно было (за какое-то число шагов) перейти в любое другое, т.е. для любых индексов i и j существует такое
, то для существования предельных вероятностей достаточно, чтобы из любого состояния системы можно было (за какое-то число шагов) перейти в любое другое, т.е. для любых индексов i и j существует такое 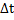 , что:
, что:
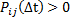
Такой марковский процесс называется транзитивным.
Однако транзитивность процесса не является необходимым условием для существования предельного режима.
ОПР. Состояние 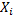 называется существенным, если нет другого состояния
называется существенным, если нет другого состояния 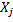 такого, что перейдя однажды каким-то способом из
такого, что перейдя однажды каким-то способом из 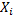 в
в 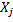 , система не может уже вернуться в
, система не может уже вернуться в 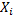 .
.
Все состояния, не обладающие таким свойством, называются несущественными.
Например, для системы X, граф состояний которой имеет вид:

|

|
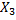
|
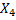
|
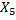
|

|
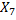
|
состояния  – несущественные (из
– несущественные (из  можно уйти, например, в
можно уйти, например, в  и не вернуться, а из
и не вернуться, а из  в
в 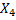 или в
или в 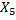 и не вернуться), а состояния
и не вернуться), а состояния  – существенные.
– существенные.
Теорема: При конечном числе состояний n для существования предельных вероятностей необходимо и достаточно, чтобы из каждого существенного состояния можно было (за какое-то число шагов) перейти в каждое другое – существенное.
Граф, представленный выше, этому условию не удовлетворяет (например, из существенного состояния 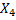 нельзя перейти в существенное состояние
нельзя перейти в существенное состояние  ).
).
Несущественное состояние потому так и называется, что из каждого такого состояния система рано или поздно уйдет в какой-то из существенных и больше не вернется. Очевидно, что предельные вероятности для несущественных состояний равны нулю.

|
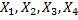 . Размеченный граф состояний, кот. имеет вид:
. Размеченный граф состояний, кот. имеет вид:

|
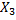
|
|
Определить является ли система эргодической и если «да», то вычислить предельные вероятности состояний.
Т.к. СП является транзитивным, то система является эргодической и существует предельный режим.
Вычислим предельные вероятности состояний:
Система уравнений Колмогорова для вероятностей состояний имеет вид:

Полагая левые части равными нулю, получим систему алгебраических уравнений для предельных вероятностей состояний.
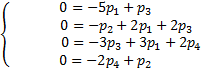
Добавляя нормировочное условие  и решая систему, находим:
и решая систему, находим:
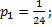

Это означает, что в установившемся режиме система X будет находиться в состоянии  в среднем 1/24 часть времени, в состоянии
в среднем 1/24 часть времени, в состоянии  – половину времени, в
– половину времени, в 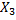 – 5/24, в
– 5/24, в 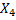 – ¼ времени
– ¼ времени
Кроме того, с помощью этих величин вычисляется критерий эффективности работы системы.
Рассмотрим два процесса, часто встречающихся на практике.
Процесс «гибели и размножения».

|

|

|

|

|
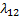
|

|

|

|

|

|

|
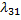
|

|

|
|

|
Т.к. процесс транзитивный, то существует предельный режим.
Уравнения Колмогорова для предельного режима имеют вид:

Преобразуя, получаем:

Добавляя нормировочное условие  и решая систему, получаем:
и решая систему, получаем:


Структура формулы:
в числителе – произведение всех интенсивностей  , стоящих у стрелок слева направо сначала и вплоть до той, которая идет в состояние
, стоящих у стрелок слева направо сначала и вплоть до той, которая идет в состояние  , в знаменателе - произведение всех
, в знаменателе - произведение всех  , стоящих у стрелок справа налево сначала и вплоть до стрелки, исходящей из состояния
, стоящих у стрелок справа налево сначала и вплоть до стрелки, исходящей из состояния  .
.
Подставляя в эти выражения нормировочное условие  , получим уравнение для определения
, получим уравнение для определения  :
:

Откуда:

Т.О.. задача решена в общем виде и найдены предельные вероятности состояний.
|

|

|

|

|
|
|

|
|
|



