Пример1. На станцию метро в данное время суток направляется простейший поток пассажиров с плотностью: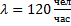 
. Найти вероятность того, что за минуту на станцию:
а) не войдет ни один пассажир:
б) войдут 1, 2, 3, 4 пассажира;
в) войдет хотя бы один пассажир.
Решение:
Т.к. поток простейший, то число пассажиров, попадающих на заданный участок τ, распределено по закону Пуассона:
вероятность того, что на участке длиной τ появится k пассажиров.
Получаем:
а) 
б) полагая k=1,2,3,4, получаем:
в) вычитая из единицы 
, получаем вероятность того, что на участке τ появится хотя бы один пассажир:
Пример2. Плотность потока вызовов на АТС зависит от времени суток и выражается формулой:
Найти вероятность того, что за промежуток времени от 17 часов до 17 часов 10 минут станция получит не менее двух вызовов.
| λ |
| 5,6 |
| t |
| λ=λ(t) |
Будем считать, что имеем нестационарный пуассоновский поток, тогда
– формула Пуассона,
где m – математическое ожидание; 
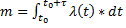- среднее число вызовов на промежутке времени ( 
.
Получаем:
Тогда вероятность того, что АТС не получит ни одного вызова или получит один вызов, равна
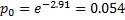
Вероятность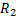 
того, что станция получит не менее двух вызовов, найдем через вероятность противоположного события – менее двух вызовов, т.е. 0 или 1 вызов.
Пример3: АТС имеет 4 линии связи. На станцию поступает простейший поток заявок с плотностью λ=3 вызов/мин. Вызов, поступивший в момент, когда все линии заняты, получает отказ. Время каждого разговора имеет показательное распределение с 
Найти:
1) вероятность отказа 
2) среднее относит. время простоя 
3) относит. пропускную способность q;
4) абсолютную пропускную способность A;
|
|
5) среднее число занятых линий во время работы АТС.
Решение:
Имеем чистую СМО с отказами, и можем использовать формулы Эрланга.
Т.к. 
то
(в среднем в систему поступает 6 заявок за время обслуживания одной заявки)
1) 
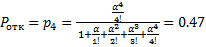
2) Среднее относит. время простоя есть 
(вероятность того, что все линии свободны)
3) q=1- 
, т.е. АТС обслуживает около 53% вызовов.
4) 4) A=λ*q=3*0.53=1.59 вызова/мин (или около 95 вызовов/час)
5) N=α(1-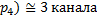 
Основы теории игр
Предмет теории игр. Основные понятия
Теория игр – математическая теория конфликтных ситуаций.
Ситуация является конфликтной, если сталкиваются две (или более) стороны, преследующие различные цели, причем результат любого мероприятия каждой из сторон зависит от того, какой образ действий примет его противник.
Схематизированную модель конфликтной ситуации называют игрой
Схематизация реальной конфликтной ситуации в теории игр состоит в выработке определенных правил игры, хорошо отражающих существ. особенности реальных конфликтов.
Стороны, участвующие в конфликте, называют игроками.
Ходом в теории игр называют выбор одного из предусмотренных правилами игры действий и его осуществление. Результат конфликта для каждой из сторон называют выигрышем игроков.
Ходы бывают личные и случайные.
Личным ходом называют сознательный выбор игроком одного из возможных вариантов действий и его осуществление.
Случайным ходом называют выбор из ряда возможностей, осуществляемый не решением игрока, а каким-либо механизмом случайного выбора.
Для каждого случайного хода правила игры определяют распределение вероятностей возможных исходов.
|
|
Некоторые игры состоят только из случайных ходов (чисто азартные игры – рулетка) или только из личных ходов (шахматы).
Большинство карточных игр содержит как личные, так и случайные ходы.
Теория игр занимается анализом только тех игр, которые содержат личные ходы. Ее задача – дать рекомендации игрокам при выборе их личных ходов, т.е. рекомендовать им определенные стратегии.
Стратегией игрока называется система правил, однозначно определяющих выбор игроком личного хода во всех возможных позициях игры.
Заметим, что стратегия – задание хода во всех возможных позициях игры – типа домашней заготовки в шахматах.
В зависимости от числа возможной стратегии игры делятся на конечные и бесконечные.
Игра называется конечно й, если у каждого игрока имеется только конечное число стратегий, и бесконечной, если хотя бы у одного из игроков имеется бесконечное число стратегий.
Стратегии игроков в тех случаях, когда они в некоторых ситуациях игры отказываются от выбора определенного хода и вместо этого используют личный случайный ход, называются смешанными стратегиями; стратегии, при которых игроки собирают только определенные ходы, называют чистыми стратегиями игроков.
При личном случайном ходе «личность» игрока проявляется в том, что игрок сам задает вероятностное распределение на множестве альтернатив, которое затем реализует механизм случайного выбора (например, подбрасывая монет, игрок задает вероятностное распределение (1/2;1/2) при выборе действия при наличии двух альтернатив).
|
|