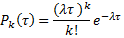Чаще встречаются ситуации, когда переходы системы из состояния в состояние происходят не в фиксированные, а в случайные моменты времени, которые заранее указать невозможно.
Отметим особенность:
вероятность перехода системы из состояния в состояние точно в момент времени t равна 0. (также как вероятность любого отдельного значения непрерывной случайной величины)
Вводят в рассмотрение плотности вероятности перехода 
ОПР. Плотностью вероятности перехода  называется предел отношения вероятности перехода системы за время Δt из состояния
называется предел отношения вероятности перехода системы за время Δt из состояния 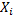 в состояние
в состояние 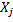 к длине промежутка Δt.
к длине промежутка Δt.
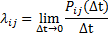
Из определения следует, что при малом Δt вероятность перехода 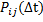 с точностью до бесконечно малых высших порядков равна:
с точностью до бесконечно малых высших порядков равна:
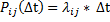
Если 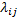 не зависит от t, марковский процесс называется однородным; если зависит – то неоднородным.
не зависит от t, марковский процесс называется однородным; если зависит – то неоднородным.
Если процесс, протекающий в системе с непрерывным временем, является марковским, то для вероятностей состояний  можно составить систему дифференциальных уравнений. Покажем, как это делается.
можно составить систему дифференциальных уравнений. Покажем, как это делается.
Пусть известны 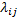 для всех пер. состояний. Построим размеченный граф:
для всех пер. состояний. Построим размеченный граф:

|
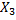
|
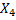
|
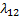
|
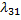
|

|
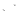
|
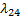
|
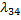
|

|
Поставим задачу: найти  - вероятность того, что в момент t система будет находиться в состоянии
- вероятность того, что в момент t система будет находиться в состоянии 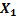 .
.
Придадим t малое приращение 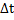 и найдем вероятность того, что в момент (t+
и найдем вероятность того, что в момент (t+ 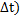 система будет находиться в состоянии
система будет находиться в состоянии 
Это событие может произойти двумя способами:
1) в момент t система находится в состоянии  и за время
и за время  не вышла из этого состояния;
не вышла из этого состояния;
2) в момент t система находится в состоянии 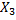 и за время
и за время 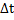 перешла из него в
перешла из него в  .
.
Вероятность первого события равна произведению вероятности того, что в момент t система находится в состоянии  , на условную вероятность того, что, будучи в состоянии
, на условную вероятность того, что, будучи в состоянии 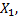 система за время
система за время 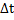 не перейдет из него в
не перейдет из него в  :
:
 *(1-
*(1- 
Аналогично, вероятность второго варианта равна:
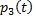 *
*  , где
, где  – условная вероятность перехода (с точностью до бесконечно малых высших порядков) за время
– условная вероятность перехода (с точностью до бесконечно малых высших порядков) за время 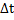 в состояние
в состояние  .
.
Применяя правила сложения вероятностей, получаем:
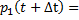
 *(1-
*(1-  +
+ 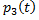 *
*  или
или
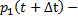
 -
- 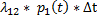 +
+ 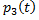 *
* 
Разделив обе части на 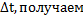
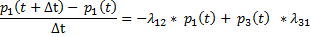
При 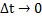 получаем:
получаем:
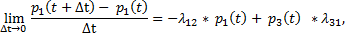
или
 - линейное ДУ первого порядка
- линейное ДУ первого порядка
Получили ДУ, которому должна удовлетворять функция  .
.
Аналогично, получаем ДУ для 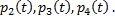
Рассмотрим второе состояние 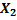 и найдем
и найдем 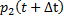 – вероятность того, что в момент времени
– вероятность того, что в момент времени 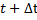 система будет находиться в состоянии
система будет находиться в состоянии 
Это событие может произойти следующими способами:
1) в момент t система находится в состоянии  и за время
и за время  не перейдет из него ни в
не перейдет из него ни в 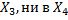 ;
;
2) в момент t система находится в состоянии  и за время
и за время 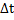 перейдет из него в
перейдет из него в  .
.
3) в момент t система находится в состоянии 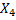 и за время
и за время 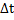 перейдет из него в
перейдет из него в  .
.
Так как события, состоящие в переходе за 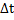 из
из  в
в 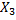 и из
и из  в
в 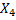 несовместны, то вероятность того, что осуществляется один из этих переходов, равна сумме их вероятностей, т.е.
несовместны, то вероятность того, что осуществляется один из этих переходов, равна сумме их вероятностей, т.е.
 +
+ 
а вероятность того, что не осуществляется ни один из этих переходов, равна:
1- 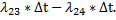
Следовательно, вероятность первого варианта равна:

Вероятность второго варианта, очевидно, равна:
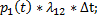
Вероятность третьего варианта равна:

По теореме сложения вероятностей получаем
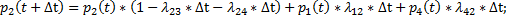
Откуда получаем:

Переходя к пределу при 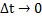 , получим
, получим
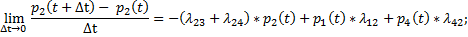
и получаем ДУ для функции 
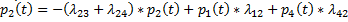
Рассмотрим состояние 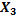 и найдем
и найдем 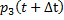 – вероятность того, что в момент
– вероятность того, что в момент 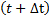 система находится в состоянии X3.
система находится в состоянии X3.
Это событие может произойти следующими способами:
1) в момент t система находится в состоянии 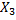 и за время
и за время 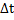 не уйдет ни в
не уйдет ни в  ни в
ни в 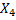 .
.
Вероятность этого события равна:

2) в момент t система находится в состоянии  и за время
и за время 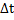 перейдет из него в
перейдет из него в 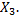 Вероятность этого события равна
Вероятность этого события равна

Тогда:
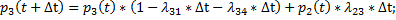
Откуда

Получаем ДУ для функции 
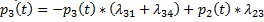
Рассмотрим состояние 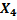 и найдем
и найдем 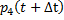
Это событие может произойти следующими способами:
1) в момент t система находится в состоянии 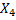 и за время
и за время 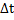 не уходит в
не уходит в  .
.
Вероятность этого события равна:
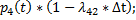
2) в момент t система находится в состоянии  и за время
и за время 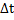 перейдет из него в
перейдет из него в 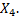 Вероятность этого события равна
Вероятность этого события равна

3) в момент t система находится в состоянии 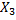 и за время
и за время 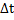 перейдет из него в
перейдет из него в 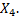 Вероятность этого события равна
Вероятность этого события равна
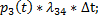
Тогда:
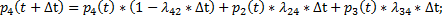
Откуда
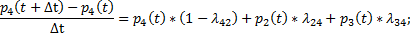
Получаем ДУ для функции 

Таким образом, получили систему дифференциальных уравнений, которые называются уравнениями Колмогорова
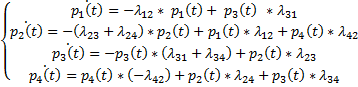 – Уравнения Колмогорова
– Уравнения Колмогорова
Решая систему с заданными начальными условиями, зависящими от начального состояния системы X, находим искомые вероятности состояний как функций времени 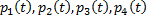
Замечание: систему можно упростить, учитывая, что 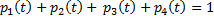 для всех t.
для всех t.
Структура уравнений показывает, что все они построены по следующему правилу:
в левой части каждого уравнения стоит производная вероятности состояния, а в правой части – столько слагаемых, сколько стрелок связано с данным состоянием.
Если стрелка направлена из состояния, слагаемое имеет знак «минус», если в состояние – знак «плюс».
Каждое слагаемое равно произведению плотности вероятности перехода, соответствующей данной стрелке, умноженной на вероятность того состояние, из которого исходит стрелка.
Правило применимо для любой непрерывной марковской цепи.
Пример:
Размеченный граф состояний системы X имеет вид, показанный на рисунке. Написать ДУ Колмогорова и начальные условия, для решения этой системы, если известно, что в начальный момент времени система находится в состоянии 
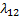
|

|

|

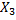
|
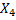
|

|
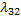
|

|
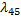
|
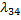
|
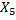
|

Начальные условия:
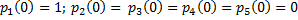
Поток событий. Простейший поток и его свойства.
Если в системе X с дискретными состояниями происходит случайный процесс с непрерывным временем, то переходы системы из состояния в состояние можно (и удобно) рассматривать как происходящие под влиянием некоторых потоков событий.
ОПР. Потоком событий называется последовательность событий, поступающих одно за другим в случайные моменты времени.
Например:
- поток воздушных целей при организации ПВО;
- поток выстрелов, направляемых на цель;
- поток вызовов на АТС;
- поток пассажиров, входящих в метро;
- поток неисправностей ЭВМ.
Поток событий называется регулярным, если событие следует одно за другим через строго определенные промежутки времени. Такие потоки не характерны, чаще встречаются случайные потоки событий, для которых и моменты наступления событий, и промежутки времени между ними случайны. Отдельные события потоков удобно изображать точками числовой оси:

|
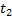
|

|

|
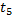
|
| t |
| τ |
Потоки событий могут обладать различными свойствами.
ОПР. Поток событий называется стационарным, если вероятность наступления к-событий на участке времени длиной τ, зависит только от длины участка и не зависит от того, где именно на оси Ot расположен этот участок, т.е.

Свойство стационарности означает, что вероятностный режим работы не меняется во времени и плотность (интенсивность) потока событий – среднее число событий в единицу времени - должна оставаться постоянной.
Лекция 3. ОПР. Поток событий называется потоком без последействия, если вероятность появления ровно k событий в интервале 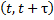 не зависит от того, сколько событий и каким образом поступило на интервале (0, t)
не зависит от того, сколько событий и каким образом поступило на интервале (0, t)
Отсутствие последействия означает независимость появления того или иного числа событий на любых неперекрывающихся участках времени.
ОПР. Поток событий называется ординарным, если вероятность поступления на малый участок времени 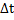 2х или более событий пренебрежимо мала по сравнению с вероятностью поступления одного события. Иными словами, вероятность поступления 2х или более событий за время
2х или более событий пренебрежимо мала по сравнению с вероятностью поступления одного события. Иными словами, вероятность поступления 2х или более событий за время 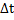 :
:

является величиной более высокого порядка малости, чем 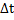 , т.е.
, т.е.
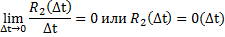
Ординарность означает практическую невозможность одновременного поступления 2х или более событий.
Поток событий, обладающий свойствами стационарности, ординарности и отсутствия последействия, называется простейшим или пуассоновским потоком!!!
Название связано с тем, что в простейшем потоке число событий, поступающих в течение заданного интервала (0,t) распределено по закону Пуассона. И вероятность  того, что число событий, поступающих в промежуток времени (0,t) равно k, определяется по формуле:
того, что число событий, поступающих в промежуток времени (0,t) равно k, определяется по формуле:
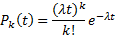
Где λ – плотность потока – среднее число событий, поступающих в единицу времени.
Заметим, что в силу стационарности простейшего потока, вероятность 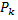 за время
за время 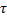 не зависит от расположения участка
не зависит от расположения участка 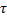 на оси Ot и вычисляется по формуле
на оси Ot и вычисляется по формуле