Моделирование операций по схеме марковских случайных процессов
Многие операции развиваются как СП, ход и результат которых зависит от ряда случайных факторов, сопровождающих эти операции. Например, функционирование системы ПВО при отражении налета, воздушны бой самолета, процесс наведения на цель УР, обслуживание клиентов в ресторане, функционирование билетных касс, работа АТС или АЗС и т.д.
ОПР. Говорят, что в физической системе Х происходит СП, если состояние системы меняется во времени случайным, заранее непредсказуемым образом.
Система Х называется системой с дискретными состояниями, если возможное состояние системы Х1, Х2, …, Хn, можно перечислить одно за другим и переход из одного состояния в другое осуществляется скачком (в дальнейшем будем рассматривать только такие системы)
Возможное состояние системы Х наглядно изображается с помощью так называемого графа состояния, на котором состояние системы изображается прямоугольниками, а возможные переходы системы из состояния в состояние – стрелками, соединяющими соответствующие прямоугольники.
| X1 |
| X4 |
| X3 |
| X2 |
Для описания СП дискретного процесса, протекающего в системе с дискретным состояниям Х1, Х2,…, Хn, пользуются вероятностями состояний


СП, протекающий в системе Х называется процессом с дискретным временем, если переходы возможны только в определенные моменты времени 
Если переходы возможны в любой момент времени, процесс называется процессом с непрерывным временем
ОПР. СП, протекающий в системе Х называется марковским (или процессом «без последствия»), если для каждого момента 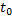 вероятность любого состояния системы в будущем(при
вероятность любого состояния системы в будущем(при  ) зависит только от ее состояния в настоящем(при
) зависит только от ее состояния в настоящем(при 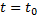 ) и не зависит от того, когда и каким образом система пришла в это состояние(т.е. как развивался процесс в прошлом – «будущее зависит от прошлого только через настоящее»)
) и не зависит от того, когда и каким образом система пришла в это состояние(т.е. как развивался процесс в прошлом – «будущее зависит от прошлого только через настоящее»)
Пусть имеется физическая система Х, которая может находиться в состояниях Х1, Х2, …, Хn, причем переходы(перескоки) системы из состояния в состояние возможны только в моменты времени  , которые называются шагами или этапами процесса
, которые называются шагами или этапами процесса
СП, происходящий в системе, состоит в том, что в последовательные моменты времени  система Х оказывается в тех или других состояниях.
система Х оказывается в тех или других состояниях.
Обозначим через  событие, состоящее в том, что после k – шагов система находится в состоянии
событие, состоящее в том, что после k – шагов система находится в состоянии  . При любом k события
. При любом k события  ,
,  образуют полную группу и несовместны.
образуют полную группу и несовместны.
Процесс, происходящий в системе, можно представить, как последовательность (цепочку) событий, например:  . Такая случайная последовательность событий называется марковской цепью, если для каждого шага вероятность перехода из любого состояния
. Такая случайная последовательность событий называется марковской цепью, если для каждого шага вероятность перехода из любого состояния  в любое
в любое  не зависит от того, когда и как система пришла в состояние
не зависит от того, когда и как система пришла в состояние  .
.
Пример 1 марковского случайного процесса с дискретным временем
По оси ОХ случайным образом перемещается точка х. В момент при t=0 т.х находится в начале координат (х(0)=0) и остается там в течение одной секунды.
Через секунду бросается монета:
· Если выпал герб - т. х перемещается на одну единицу длины вправо;
· Если цифра – влево
Через секунду снова бросается монета и производится такое же случайное перемещение и т.д.
| -3 -2 -1 0 1 2 3 t |
Процесс изменения положения точки представляет собой СП с дискретным временем(t=0, 1, 2, 3…) и счетным множеством состояний 

|

|

|

|
- граф состояний
Процесс – марковский.
Действительно пусть в момент времени 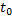 система, находится, например, в состоянии
система, находится, например, в состоянии 
Возможные положения точки через единицу времени будут  с вероятностями ½ и ½, а через 2 единицы времени возможные положения точки:
с вероятностями ½ и ½, а через 2 единицы времени возможные положения точки:  с вероятностями ¼, ½, ¼ и т.д.
с вероятностями ¼, ½, ¼ и т.д.
Очевидно, все эти вероятности зависят только от того, где находится точка в данный момент  и совершенно не зависит от того, как она туда пришла.
и совершенно не зависит от того, как она туда пришла.
Будем описывать марковскую цепь с помощью вероятностей состояний:

вероятности 
состояний после …..
1-го шага и т.д. 
 -
-
- вероятности состояний после K-ого шага, причем для каждого номера шага K выполняется равенство:
 , так как это вероятности несовместимых событий, образующих полную группу.
, так как это вероятности несовместимых событий, образующих полную группу.
Поставим задачу: найти вероятности состояний системы для любого k.
Вероятности перехода системы из любого состояния  в любое другое
в любое другое  называют переходными вероятностями
называют переходными вероятностями 

Марковская цепь называется однородной, если переходные вероятности не зависят от номера шага, иначе марковская цепь назыв. неоднородной.
Переходные вероятности  записываются в виде прямоугольной матрицы:
записываются в виде прямоугольной матрицы:

Система состоит из n возможных состояний 
При рассмотрении марковских цепей пользуются графом состояний, на котором у стрелок проставлены соотв. переходные вероятности, например

|

|
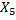
|
|

|

|

|

|

|

|

|

|

|

|

|
|

|
Такой граф называют размеченным графом состояний.
Представляются не все переходные вероятности, а только те из них, которые не равны 0 и меняют состояния системы.
Вероятности «задержки"  на графы также не проставляют, так как каждая из них дополняет до единицы сумму переходных вероятностей, соответствующих всем стрелкам, исходящим из данного состояния:
на графы также не проставляют, так как каждая из них дополняет до единицы сумму переходных вероятностей, соответствующих всем стрелкам, исходящим из данного состояния:


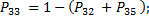


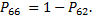
Если из состояния  не исходит ни одной стрелки (переход невозможен), то
не исходит ни одной стрелки (переход невозможен), то 
Имея размеченный граф состояний (т.е. матрицу  и зная начальное состояние системы), можно найти вероятности состояний
и зная начальное состояние системы), можно найти вероятности состояний  после любого K-ого шага.
после любого K-ого шага.
Пусть в начальный момент система находится в состоянии  , тогда
, тогда

Найдем вероятности состояний после первого шага

Найдем вероятности состояний после второго шага по формуле полной вероятности (формуле гипотез). Имеем:


После 3-го шага:

После k-го шага:

Замечание: если марковская я цепь неоднородна и вероятности перехода  меняются от шага к шагу, то матрицы вероятностей перехода задают на каждом шаге, а формула принимает вид:
меняются от шага к шагу, то матрицы вероятностей перехода задают на каждом шаге, а формула принимает вид:

Лекция 2. Пример
По цели ведется стрельба 4мя выстрелами в моменты времени  ,
, 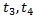
Возможное состояние цели:
 цель не поражена;
цель не поражена;
 цель слабо повреждена;
цель слабо повреждена;
 цель сильно повреждена;
цель сильно повреждена;
 цель уничтожена;
цель уничтожена;

|

|
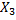
|
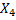
|
| 0,4 |
| 0,1 |

|

|

|

|
В начальный момент цель находится в состоянии 
Определить вероятности состояния цели после 4х выстрелов.
Из графа состояний получаем матрицу переходных состояний

Начальные условия:


После первого обстрела вероятности состояний будут равны:

После второго обстрела:
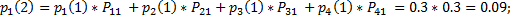



После третьего обстрела:




После четвертого обстрела:




Т. О. после четырех обстрелов:
- цель не повреждена с вероятностью 
-цель слабо повреждена с вероятностью 
- цель сильно повреждена с вероятностью 
-цель уничтожена с вероятностью  .
.
Вероятности состояний – это функции времени!!!