Лекция 5. Циклический процесс

ОПР. Марковский СП, протекающий в системе, называется циклическим, если состояния связаны между собой в кольцо (цикл) с односторонними переходами.

 

…

…

 

 

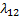
Т.к. процесс транзитивный, то существует предельный режим. Уравнения Колмогорова для предельного режима имеют вид:

Добавляя условие и решая систему, получаем:

Подставляя эти значения в нормировочное условие, получаем уравнение относительно , откуда находим:

Упростим вид формулы.

Для этого перейдем от интенсивности к средним временам пребывания системы в состоянии

Пусть система находится в состоянии

 

 

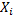
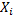
Найдем математическое ожидание времени , которое она пробудет еще в этом состоянии.

Т.к. промежуток времени T между соседними событиями в простейшем «потоке уходов» системы из состояния 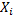распределен по показательному закону, то:

Отсюда для всех i=1,2,…,n-1

Для i=n, в силу цикличности,

Подставляя в формулы и преобразуя, получаем:

т.е. , где k=1,2,…,n

Т.е. предельные вероятности состояния в циклической системе относятся как средние времена пребывания системы подряд в каждом из состояний.

Приближенное сведение немарковских процессов к марковским.

Метод «псевдосостояний»

На практике марковские процессы в чистом виде встречаются очень редко: реальные процессы почти всегда обладают тем или иным последействием. Кроме того, время пребывания системы в каком-либо состоянии не всегда распределено по показательному закону.

Возникает вопрос:

Можно ли приближенно заменять непуассоновские потоки пуассоновским и к каким ошибкам в предельных вероятностях состояний может привести подобная замена?

В некоторых случаях это возможно:

если число состояний системы не очень велико, а потоки событий, участвующие в задаче, представляют собой потоки Эрланга.

Тогда, вводя в схему возможных состояний системы некоторые фиктивные «псевдосостояния», удается свести немарковский процесс к марковскому и описать его с помощью уравнений Колмогорова.

Поясним идею метода «псевдосостояний» на примере.

Пример: рассматривается система X – техническое устройство, кот. может выходить из строя под влиянием простейшего потока неисправностей с интенсивностью . Отказавшее устройство сразу же начинает ремонтироваться. Время ремонта T распределено не по показательному закону, а по закону Эрланга второго порядка:

(поэтому процесс немарковский)

Требуется свести данный немарковский процесс к марковскому и найти для него предельные вероятности состояний.

Решение:

Т.к. СВ T – время ремонта, распределено по закону Эрланга второго порядка, то оно представляет собой сумму трех независимых СВ , распределенных по показательному закону с параметром :

Истинных состояний системы 2:

- устройство исправно;

– устройство ремонтируется

λ

Граф этих состояний имеет вид:

Переход по стрелке происходит под влиянием не простейшего, а эрланговского потока событий, поэтому процесс, происходящий в системе, не будет марковским и мы не можем написать уравнения Колмогорова для вероятностей состояний.

Чтобы искусственно свести этот процесс к марковскому, введем в цепочку состояний вместо одного состояния три последовательных «псевдосостояния»:

– первый этап ремонта (ремонт начинается)

– второй этап ремонта (ремонт продолжается)

– третий этап ремонта (ремонт заканчивается)

λ

Т.О. разделили ремонт на три этапа или фазы, причем время пребывания системы в каждой из фаз распределено по показательному закону. Процесс, протекающий в такой системе, будет уже марковским, а соответствующий граф состояний будет иметь вид:

Процесс циклический, обозначая

получаем:

Или