Содержание работы:
1) Сформировать таблицу по следующей форме:
| № п/п | х | Имя функции 1 | Имя функции 2 | Имя функции 3 |
Для ввода символа № надо переключить клавиатуру на русский алфавит и нажать одновременно две клавиши: Shift + # (№).
В заголовках «Имя функции» ввести конкретные имена функций согласно своему варианту. Варианты заданий приведены в таблице 2.1.
В столбце «№ п/п» для получения порядковых номеров использовать формулу =строка()-k,где k– это количество строк, расположенных выше строки, в которую вводится формула.
В столбце «х» ввести формулу =а+(i-1)*h, где:
· а – начальное значение х;
· i – адрес ячейки, в которой записана формула =строка()-k;
· h – шаг, на который увеличивается значение аргумента х.
В столбцы с заголовками функций ввести формулы, используя первый способ (ввод функции непосредственно в ячейку). Ввод функции начинается с символа = (равно). Для ввода аргумента функции достаточно щёлкнуть мышью по ячейке со значением х, то есть по ячейке, в которую введена формула =а+(i-1)*h.
Пример:
| B | C | D | E | F | |
| № п/п | x | Sin(x) | Cos(x) | Exp(x) | |
| =СТРОКА()-4 | =0+(A5-1)*0,1 | =SIN(C4) | =COS(C4) | =EXP(C4) |
Функция корень(х) неопределена при х<0, поэтому при вычислении её значений надо воспользоваться функцией если().
Пример: =если(c4>0;корень(c4);”Не сущ.”)
Функции ln(x) и log10(x) неопределены при x £0, а функции asin(x) и acos(x)при | x |>1, поэтому при их применении надо также воспользоваться функцией если().
Примеры: =если(c4>0;ln(c4);”Не сущ.”)
=если(c4>0;log10(c4);”Не сущ.”)
=если(abs(c4)<=1;asin(c4);”Не сущ.”)
=если(abs(c4)<=1;acos(c4);”Не сущ.”)
После заполнения первой строки таблицы формулами необходимо выполнить следующие действия:
· Щёлкнуть мышью по ячейке первого столбца и первой строки таблицы. Ячейка станет активной. Указатель мыши установить на правый нижний угол рамки этой ячейки (чёрный крестик). Это маркер заполнения. Нажать левую кнопку мыши, поймать черный крестик и при нажатой левой кнопке мыши протянуть ячейку по столбцу вниз так, чтобы в таблице получилась 20 строк.
· Выполнить аналогичные операции в остальных столбцах до 15 строки таблицы включительно.
2) Во втором столбце таблицы ввести: в 16 строке слово
Количество, в 17 строке слово Сумма, в 18 строке текст Ср.значение, в 19 строке слово Максимум и в 20 строке слово Минимум.
3) Вычислить по столбцу D значения всех пяти величин согласно пункту 2, используя кнопку Автосумма(Σ) на панели инструментов Стандартная. В меню этого инструмента имеются строки Ч исло, С уммировать, Ср е днее, М а ксимум, М инимум,которые обеспечивают вычисление соответствующих значений.
4) Вычислить по столбцам E и F значения всех пяти величин согласно пункту 2, используя Мастер функций (кнопка fx).
5) Оформить рамку таблицы. Для этого выделить все заполненные ячейки, установив указатель мышки на левую верхнюю ячейку, нажать левую кнопку мыши и протащить до правой нижней ячейки. Выделенный диапазон ячеек будет заключён в общую рамку, а фон диапазона ячеек будет иметь определённый цвет, например, синий, кроме первой ячейки. Щелкнуть мышью по стрелке у кнопки Границы на панели инструментов Форматирование (чёрный маленький треугольник вершиной вниз). В появившейся форме щёлкнуть по кнопке Все границы. Для размещения содержимого ячеек по центру надо выделить весь диапазон ячеек таблицы и на панели инструментов Форматирование щёлкнуть мышью по кнопке По центру.
6) Создать диаграмму с графиками всех трёх функций, для чего выполнить следующие действия:
· Выделить диапазон ячеек B6:E20.
· Щёлкнуть мышью по кнопке Мастер диаграмм на панели инструментов Стандартная и в появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы при закладке Стандартные в окне Тип щёлкнуть по строке
Точечная, в окне Вид щёлкнуть по правому образцу графика (гладкие графики) и внизу формы щёлкнуть по кнопке Далее. Уяснить все возможности этого шага.
· В диалоговом окне Мастер диаграмм (шаг 2 из 4):
источник данных диаграммы, просмотрев образец графиков, щёлкнуть по кнопке Далее. Если образца графиков нет или содержимое не соответствует исходным данным, то необходимо откорректировать диапазоны ячеек по оси X и по оси Y поочерёдно для всех трех функций. Уяснить все возможности этого шага.
· В диалоговом окне Мастер диаграмм (шаг 3 из 4):
параметры диаграммы при закладке Заголовки в окно
Название диаграммы ввести текст Графики функций, в окно Ось Х (категорий) ввести Х, в окно Ось Y (значений) ввести Y. Щёлкнуть по кнопке Линии сетки и под заголовком Ось Х (категорий) установить флажок в окне основные линии. В завершение щёлкнуть по кнопке Далее. Уяснить все возможности этого шага.
· В диалоговом окне Мастер диаграмм (шаг 4 из 4): размещение диаграммы уяснить все варианты размещения, а затем, ничего не изменяя, щёлкнуть по кнопке Готово.
· Установить указатель мыши в поле Область диаграммы и, нажав левую кнопку мыши, переместить диаграмму вправо (через столбец от таблицы). Затем установить указатель мыши на чёрный квадратик (маркер масштабирования) в середине верхней стороны рамки вокруг диаграммы и, нажав на левую кнопку мыши, растянуть диаграмму вверх до начала таблицы. Такую же операцию выполнить и для нижней стороны рамки.
· Название оси Y переместить вверх по оси и выровнять, а название оси Х вправо от самой оси. Для чего установить указатель мыши на название оси и нажать левую кнопку мыши, а затем, зацепив мышью за край рамки, перетащить этот элемент диаграммы (название оси) в указанное место. Для выравнивания названия оси Y надо его снова выделить и щёлкнуть на нем правой кнопкой мыши. В появившемся меню щёлкнуть по строке Ф ормат
названия оси…. В диалоговом окне Формат названия оси щёлкнуть по кнопке Выравнивание, а затем по точке
0 градусов. В завершение щёлкнуть по кнопке OK.
· Отформатировать остальные элементы диаграммы: увеличить толщину осевых линий, линий графиков и установить разные цвета линиям графиков. При этом в соответствующем диалоговом окне щёлкнуть по кнопке Вид и в окне толщина выбрать средний вариант, а для выбора цвета линий графиков щёлкнуть по кнопке Цвет. В завершение щёлкнуть по кнопке OK.
Варианты задания
Таблица 2.1
| № вар. | Нач. х | Шаг | Функция 1 | Функция 2 | Функция 3 |
| -0,1 | 0,1 | Sin(x) | Atan(x) | Log10(x) | |
| -0,1 | 0,1 | Cos(x) | Exp(x) | КОРЕНЬ(х) | |
| 0,1 | Atan(x) | Exp(x) | Ln(x) | ||
| -0,1 | 0,2 | Tan(x) | Atan(x) | Log10(x) | |
| -0,1 | 0,2 | Exp(x) | Abs(x) | Ln(x) | |
| -0,2 | 0,2 | Sin(x) | Cos(x) | КОРЕНЬ(х) | |
| -0,2 | 0,2 | Abs(x) | Atan(x) | Ln(x) | |
| 0,1 | Exp(x) | Atan(x) | Log10(x) | ||
| -0,2 | 0,2 | Cos(x) | Atan(x) | КОРЕНЬ(х) | |
| 0,1 | Tan(x) | Abs(x) | Ln(x) | ||
| 0,05 | Exp(x) | Atan(x) | Log10(x) | ||
| -0,05 | 0,05 | Tan(x) | Cos(x) | КОРЕНЬ(х) | |
| 1,1 | 0,1 | Cos(x) | Atan(x) | ACOS(x) | |
| -1,1 | 0,1 | Sin(x) | Atan(x) | ASIN(x) | |
| -1,1 | 0,1 | Cos(x) | Exp(x) | ACOS(x) | |
| -0,1 | 0,1 | Atan(x) | Exp(x) | Ln(x) | |
| -1,2 | 0,2 | Tan(x) | Atan(x) | ASIN(x) | |
| -0,1 | 0,2 | Exp(x) | Abs(x) | Ln(x) | |
| -0,2 | 0,2 | Tan(x) | Cos(x) | КОРЕНЬ(х) | |
| -0,2 | 0,2 | Abs(x) | Atan(x) | Ln(x) | |
| 0,1 | Exp(x) | Atan(x) | Log10(x) | ||
| -0,2 | 0,2 | Cos(x) | Exp(x) | КОРЕНЬ(х) | |
| -1,2 | 0,2 | Tan(x) | Abs(x) | ASIN(x) | |
| 0,05 | Exp(x) | Atan(x) | Log10(x) | ||
| -0,05 | 0,05 | Tan(x) | Atan(x) | КОРЕНЬ(х) |
Продолжение таблицы 2.1
| № вар. | Нач. х | Шаг | Функция 1 | Функция 2 | Функция 3 |
| -0,2 | 0,2 | Abs(x) | Atan(x) | Ln(x) | |
| -0,1 | 0,1 | Sin(x) | Atan(x) | Log10(x) | |
| -0,1 | 0,1 | Cos(x) | Exp(x) | КОРЕНЬ(х) | |
| 0,1 | Atan(x) | Exp(x) | Ln(x) | ||
| -0,1 | 0,2 | Tan(x) | Atan(x) | Log10(x) |
Примечание: номер варианта соответствует номеру студента в списке учебной группы. Примерное оформление рабочего листа приведено в приложении 1.
2.4. Применение стандартных функций с несколькими
аргументами
К числу функций с несколькими аргументами относится функция РЯД.СУММ(x; n; m; коэффициенты) – возвращает сумму членов функционального степенного ряда, где:
x – значение переменной степенного ряда;
n – показатель степени хдля первого члена степенного ряда;
m – шаг, на который увеличивается показатель степени n для каждого следующего члена степенного ряда;
коэффициенты – это коэффициенты (числа) при соответствующих членах степенного ряда, записанные в определённые ячейки рабочего листа. В списке аргументов функции они задаются в виде ссылки на диапазон ячеек, например, A2:A6.
Пример: =РЯД.СУММ(B2;B3;B4;B5:B10)
В ячейках B2–B10 записаны значения указанных выше параметров функции.
Для доступа к этой функции (и некоторым другим) необходимо подключить надстройку Пакет анализа.
Для установки надстройки Пакет анализа необходимо выполнить следующие действия:
· щелчком мыши открыть меню С е рвис;
· в открывшемся меню щёлкнуть мышью по строке
Надстро й ки…;
· в открывшемся окне установить флажок в окошечке строки
Пакет анализа и щёлкнуть мышью по кнопке OK.
Если при использовании функции в ячейке отображается константа ошибки #ИМЯ?, то, возможно, не установлен Пакет анализа. Подробности можно найти в С правке по этой функции.
Примечание: при вычислении функции РЯД.СУММ(x; n; m; коэффициенты) для некоторых вариантов следует использовать функции: ФАКТР(x), КОРЕНЬ(x) и СТЕПЕНЬ(x;n). Варианты заданий приведены в таблице 2.2.
Пример вычисления суммы ряда (вариант № 30)
| B | C | |
| x= | 1,25 | |
| n= | ||
| m= | ||
| a1= | ||
| a2= | =1/фактр(3) | |
| a3= | =1/фактр(5) | |
| a4= | =1/фактр(7) | |
| a5= | =1/фактр(9) | |
| S= | =ряд.сумм(с23;c24;c25;c26:с30) |
Варианты задания
Таблица 2.2
| № вар. | Члены функционального степенного ряда | х |
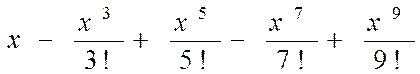
| 0,5 | |
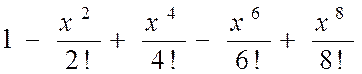
| 0,5 | |

| 0,5 | |
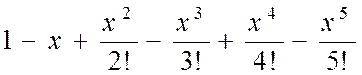
| 0,5 | |

| 0,5 | |

| 0,5 | |
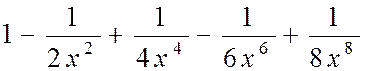
| 0,5 | |

| 0,5 | |
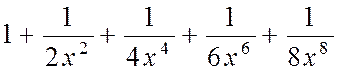
| 0,5 |
Продолжение таблицы 2.2
| № вар. | Члены функционального степенного ряда | х |
 
| 0,5 | |
 
| 0,5 | |

| 1,5 | |
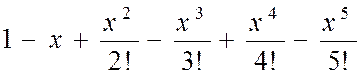
| 1,5 | |

| 1,5 | |
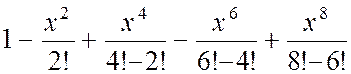
| 1,5 | |
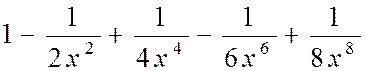
| 1,5 | |
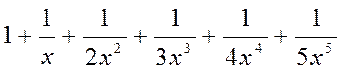
| 1,5 | |
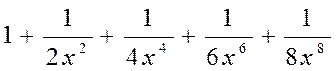
| 1,5 | |

| 1,5 |
Продолжение таблицы 2.2
| № вар. | Члены функционального степенного ряда | х |
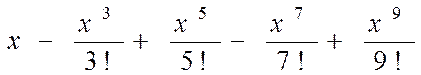
| 1,5 | |
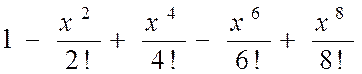
| 1,5 | |

| 1,25 | |
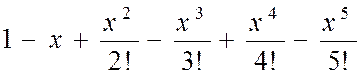
| 1,25 | |

| 1,25 | |

| 1,25 | |
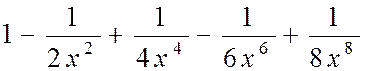
| 1,25 | |

| 1,25 | |
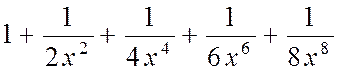
| 1,25 | |
 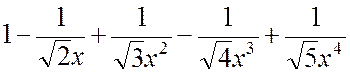
| 1,25 |
Продолжение таблицы 2.2
| № вар. | Члены функционального степенного ряда | х |
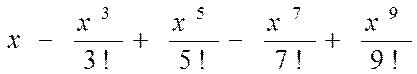
| 1,25 |
3. ЛАБОРАТОРНАЯ РАБОТА № 2
«АППРОКСИМАЦИЯ ФУНКЦИИ»
Цель работы: овладеть приёмами и правилами работы с Мастером диаграмм.
Сущность аппроксимации (подбора зависимостей) состоит в том, чтобы на основе имеющихся двух числовых рядов, которые можно представить как значения по оси X (независимая переменная) и по оси Y (зависимая переменная), получить соответствующее выражение для подбираемой функциональной зависимости Y от X. На практике такая задача может возникнуть при проведении каких-либо опытов, экспериментов, испытаний устройств и других подобных действий.