В примере на рис.3.1 урожайности зерновых в России за 200 лет присутствие гетероскедастичности не вызывает сомнений, достаточно взглянуть на рисунок. Однако во многих случаях обнаружение гетероскедастичности визуально не столь очевидно. Чтобы определить, присутствует ли гетероскедастичность на самом деле, применяют различные тесты.
Все тесты основаны на предположении о наличии связи между дисперсиями остатков моделей и объясняющими переменными или расчетными значениями зависимой переменной в случае гетероскедастичности.
Эта связь обнаруживается с помощью коэффициента ранговой корреляции в тесте ранговой корреляции Спирмена, либо предполагается пропорциональность стандартных отклонений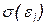 
и зависимой переменной Y в тесте Голдфелда-Квандта, либо строятся различные линейные и нелинейные регрессии 
, 2, 
на объясняющие переменные или степени зависимой переменной Y и проверяется значимость полученных коэффициентов регрессии в тестах Анскомба, Рамсея, Уайта и Глейзера. В асимптотическом тесте Бреуша и Пагана (Breusch and Pagan) проверяется по критерию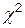 
(r) значимость величины 
, где 
, а 
— сумма квадратов объясняемая произвольного вида регрессией 
на некоторые переменные 
.
Тест Голдфелда-Квандта. ( Goldfeld-Quandt) Этот тест предполагает, что ошибки регрессии 
являются выборочными значениями нормально распределенной случайной величины. В случае гомоскедастичности первая треть наблюдений и последняя треть наблюдений имеют одинаковые дисперсии. С помощью критерия Фишера-Снедекора эта гипотеза проверяется.
Строится наблюдаемое значение критерия
.
Если 
, где 
-уровень значимости, 
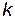-число объясняющих переменных (регрессоров), 
— табличное значение критерия Фишера, то гипотеза о гомоскедастичности отвергается на -процентном уровне. В противном случае нет оснований отвергнуть нулевую гипотезу о гомоскедастичности остатков модели.
|
|
Тест ранговой корреляции Спирмена. Тест Спирмена не требует предположения нормальности распределения регрессионных остатков. Проверяется лишь предположение, что в случае гетероскедастичности остатки коррелированны со значениями регрессоров или расчетными значениями зависимой переменной. Для нахождения коэффициента ранговой корреляции следует предварительно ранжировать наблюдения по одной из объясняющей переменной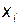 
или расчетные значения зависимой переменной 
и ранжировать остатки 
. Далее вычисляется выборочное значение коэффициента корреляции Спирмена по формуле: 
, где 
— разности между рангами значени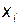й и , и проверяется значимость коэффициента корреляции. Гетероскедастичность считается доказанной на уровне значимости , если наблюдаемое значение критерия Стьюдента
,
где 
- табличное значение критерия Стьюдента при уровне значимости и с числом степеней свободы равном 
.
Рассмотрим пример. На рис. 4.1 дан график изменения урожайности пшеницы в США с 1866 по 1998 годы. Аппроксимируем ряд моделью вида 
. Расчеты выполнялись в модуле Нелинейная регрессия пакета STATISTICA. Получим уравнение
.
В модуле Непараметрические статистики, сохранив предварительно остатки и расчетные значения модели, рассчитаем значение коэффициента ранговой корреляции Спирмена и его значимость.
Рис. 4.1. Урожайность пшеницы в США с 1866 по 1998 гг.
|
|
Таблица 4.1
Из результатов таблицы вытекает значимость коэффициента Спирмена и, следовательно, гетероскедастичность остатков модели.