В теореме Гаусса-Маркова предполагалось, что случайные возмущения имеют постоянную дисперсию и не коррелированы друг с другом. Это означает, что ковариационная матрица имеет вид: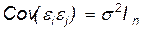 
, где 
— единичная матрица размерности n. Если существует корреляция между ошибками наблюдений или дисперсия ошибок наблюдений не предполагается постоянной, то мы оказываемся в условиях обобщенной линейной модели множественной регрессии.
Обобщенная линейная модель множественной регрессии предполагает следующую систему соотношений и условий:
1) 
; 
.
Ранг неслучайной (детерминированной) матрицы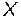 
предполагается равным p + 1 < n, p — число предикторов, 
случайный вектор, n — число наблюдений;
2) 
- где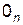 
— матрица размера n´n состоящая из нулей.
3) 
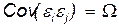, где 
— положительно определенная матрица. Это означает, что определители всех главных миноров матрицы положительны. Напомним, что главными минорами матрицы являются миноры вида:
.
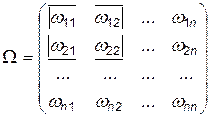Итак, в обобщенной линейной регрессионной модели дисперсии и ковариации ошибок наблюдений могут быть произвольными.
Доказано, что при применении обычного МНК для построения оценок коэффициентов в условиях обобщенной модели получается смещенная оценка ковариационной матрицы 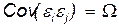. Поэтому, оценки коэффициентов модели полученные по методу МНК будут несмещенными, состоятельными, но не эффективными. Для получения эффективных оценок нужно использовать оценки коэффициентов полученных на основе других методов, например, на основе обобщенного метода наименьших квадратов ОМНК.
Теорема Айткена. В классе линейных несмещенных оценок вектора коэффициентов модели 
оценка
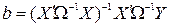(4.2)
является эффективной.
Доказательство состоит в сведении условий теоремы Айткена к условиям теоремы Гаусса–Маркова путем соответствующих преобразований и введения вспомогательных переменных-векторов. Представим (4.2) в виде
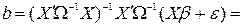
(4.3)
Из (4.3) и условия вытекает несмещенность оценки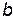 
. Далее, матрица W является симметричной, то есть 
, и невырожденной, то есть ее определитель не равен нулю. Из теории матриц вытекает, что существует, по крайней мере, одна невырожденная матрица 
такая, что 
. Тогда по свойству обратных матриц справедливо равенство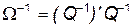 
.
Умножим обе части обобщенной регрессионной модели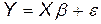 
слева на матрицу 
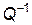. Получаем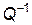 
. Введем новые вспомогательные переменные:
; 
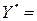
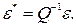(4.4)
Проверим, что уравнение (4.4) удовлетворяет условиям Гаусса-Маркова и, следовательно, МНК оценки для коэффициентов уравнения (4.4) эффективные. Но легко проверить, что МНК оценки для коэффициентов уравнения (4.4) являются оценками (4.2) обобщенного МНК для уравнения 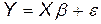. То есть теорема Айткена будет нами доказана. Проверим, что 
Имеем,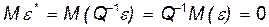 
, что и требовалось. Далее
(4.5)
Проверим, наконец, что МНК оценка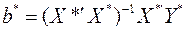 
является ОМНК оценкой для исходных переменных. Имеем
=
= 
,
то есть мы получили оценку (4.2). Доказательство теоремы завершено.
Так как оценка (4.2) согласно МНК минимизирует остаточную сумму квадратов
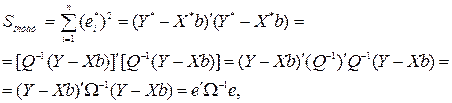(4.6)
то оценка ОМНК является точкой минимума обобщенного критерия (4.6).
Устранение гетероскедастичности путем применения ОМНК требует знания матрицы ковариаций ошибок наблюдений, что бывает на практике в исключительных случаях. Если же считать все элементы матрицы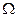 
неизвестными величинами, то число неизвестных вместе с параметрами модели будет равно 
, то есть превысит число наблюдений. Поэтому, в общем случае, задача одновременного нахождения параметров модели и ковариационной матрицы ошибок наблюдений неразрешима. Приходится накладывать дополнительные ограничения на структуру ковариационной матрицы 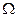. Чаще всего предполагается, что ковариационная матрица вектора случайных ошибок диагональная, то есть
. (4.7)
Если дисперсии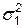 
, 
, …, 
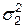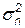известны, то применение обратной матрицы 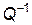к уравнению регрессии МНК сводится к делению переменных модели в i -ом наблюдении на 
. Такой метод расчета коэффициентов модели называется взвешенным МНК. В этом случае минимизируется сумма
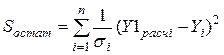. (4.8)
В реальных экономических задачах значения неизвестны. Поэтому точные значения заменяют их оценками . Сначала получают уравнение регрессии с помощью обычного МНК. Затем строят уравнение регрессии квадратов остатков 
на квадраты объясняющих переменных и их попарные произведения. Получают расчетные (прогнозные) значения . Наконец, веса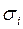 
находят по формуле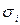 
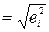. Возможен и подход Глейзера, в котором строятся регрессии модулей остатков обычной МНК модели на объясняющие переменные в различных степенях. Выбирается наиболее значимая регрессия и ее прогнозные значения берут за веса в ОМНК модели.
4.6. Контрольные вопросы к главе 4 «Гетероскедастичность моделей, ее обнаружение и методы устранения гетероскедастичности»
1. Дайте определение гетероскедастичности наблюдений.
2. Расскажите о тестировании гетероскедастичности на основе теста Голдфелда-Кванта.
3. Опишите как применяется для обнаружения гетероскедастичности тест ранговой корреляции Спирмена.
4. Каковы последствия гетероскедастичности в случае при использования МНК для построения модели?
5. Опишите подходы к устранению гетероскедастичности основанные на преобразовании исходных данных.
6. Сформулируйте теорему Айткена о коэффициентах обобщенного МНК.
7. Опишите алгоритм обобщенного метода наименьших квадратов (ОМНК) для построения уравнения регрессии в случае гетероскедастических наблюдений.