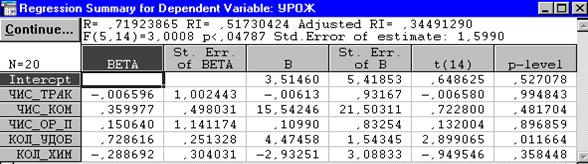
 |
Уравнение множественной регрессии имеет вид:
УРОЖ = 3,515 – 0,006 ЧИС_ТРАК +15,542ЧИС_КОМ +
(с. о) (5,42) (0,93) (21,5)
+ 0,110ЧИС_ОР_П + 4,475КОЛ_УДОБ – 2,933КОЛ_ХИМ;
(0,83) (1,54) (3,09)
= 0,517
Таблица 3.37
 |
Уравнение множественной регрессии
Полученное уравнение регрессии значимо на стандартном 5 % уровне (p–значение равняется 0,047) и оно объясняет примерно 52 % вариации зависимой переменой при пяти включённых в модель объясняющих переменных. Однако это уравнение не позволяет оценить вклад каждой из переменных, входящих в это уравнение, поскольку почти все, кроме переменной КОЛ_УДОБ не значимы. Такое положение является следствием мультиколлинеарности, вызванной тесной корреляционной связью между переменными, на которых строилось регрессионное уравнение. В этом можно убедиться, анализируя матрицу парных коэффициентов корреляции.
Для устранения мультиколлинеарности можно применить процедуру пошагового отбора переменных. Рассмотрим два подхода, реализованных в пакете STATISTICA.
1. Пошаговая процедура последовательного присоединения переменных. (Forward stepwise).
 |
Таблица 3.38
Первый шаг процедуры Forward stepwise
На первом шаге в модель была включена переменная КОЛ_УДОБ, имеющая с результирующей переменной УРОЖ наибольший квадрат коэффициента корреляции - = 0,333 (
= 0,577).
Таблица 3.39
Второй шаг процедуры Forward stepwise
 |
На втором шаге была добавлена переменная ЧИС_ОР_П. Полученное уравнение, также как и первое, значимо на стандартном 5 % уровне. Все коэффициенты, входящих в уравнение переменных, значимо отличны от нуля.
Сравнивая полученное уравнение с предыдущим, отметим, что возросло не только значение коэффициента детерминации ( = 0,482), но и значение скорректированного коэффициента (
= 0,421), что весьма существенно. При этом стандартные ошибки уравнений регрессии различаются мало –1,6573 и 1,5027. Общий ход выполнения пошаговой процедуры включения отражен в таблице 3.40.
 |
Таблица 3.40
Ход выполнения пошаговой процедуры Forward stepwise
2. Пошаговая процедура последовательного удаления (исключения) переменных (Backward stepwise).
0 шаг. На этом шаге рассматривается уравнение регрессии, включающее весь набор исходных переменных.
Таблица 3.41
 |
Начальный шаг процедуры Backward stepwise
Все последующие шаги этой процедуры приведены ниже в таблицах 3.42 - 3.45.
Таблица 3.42
 |
1 шаг
Таблица 3.43
 |
2 шаг
Таблица 3.44
 |
3 шаг
Таблица 3.45
 |
4 шаг
Общий ход выполнения пошаговой процедуры исключения отражен в таблице, представленной в таблице 3.46 и рис. 3.13.
Таблица 3.46
 |
Общий ход выполнения пошаговой процедуры Backward stepwise
 |
Рис. 3.13. График скорректированных коэффициентов детерминации,
полученных при выполнении пошаговой процедуры
На графике представлены значения скорректированного коэффициента детерминации , полученные в ходе выполнения процедуры пошагового удаления переменных. Наилучшим вариантом следует признать тот, при котором достигается наибольшее значение скорректированного коэффициента детерминации, т.е. вариант, полученный на 2-ом шаге процедуры пошагового удаления переменных. Это уравнение имеет вид:
УРОЖ = 1,980 + 21,801ЧИС_КОМ + 4,614КОЛ_УДОБ
(с. о) (2,50) (8,96) (1,38)
– 3,380КОЛ_ХИМ; =0,513
(2,57)
Стандартизированное уравнение регрессии для этого набора переменных выглядит следующим образом:
УРОЖ = 0,505ЧИС_КОМ + 0,751КОЛ_УДОБ - 0,329 КОЛ_ХИМ.
Анализ коэффициентов этого уравнения позволяет сравнить степени влияния на результирующий показатель объясняющих переменных. Так, влияние переменной КОЛ_УДОБ (количество удобрений, вносимых на гектар) на величину урожая при постоянных средних значениях других показателей примерно в 1,5 раза выше, чем переменной ЧИС_КОМ — (число комбайнов). Влияние переменной КОЛ_ХИМ (количество химических средств защиты растений, расходуемых на гектар), интерпретировать не следует ввиду не значимости этого показателя в уравнении регрессии. Отметим, что при проведении шаговой процедуры включения эта объясняющая переменная не была включена в регрессионную модель.
Таблица 3.47
Результаты расчета коэффициентов толерантности и детерминации,
 |
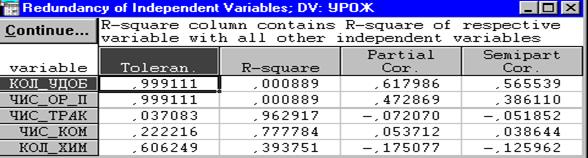полученные в ходе пошаговых процедур
Анализ этой таблицы позволяет судить об избыточности входящих в уравнение переменных. Так, две первые переменные довольно слабо связаны со всеми остальными. Об этом свидетельствует коэффициент множественной детерминации связи этих переменных со всем набором остальных переменных. И наоборот, последние три переменные имеют довольно тесную связь со всеми другими переменными, что и обусловливает в свою очередь наличие мультиколлинеарности (Toleran = 1 – R -square).
К аналогичному выводу можно придти, анализируя частные коэффициенты корреляции (Partial Cor.). Первые две переменные имеют более тесную связь с зависимой переменной, чем остальные три переменные.