Выше мы предполагали, что объясняющие переменные модели могут принимать любые значения в некотором интервале данных. Такие переменные будем называть количественными переменными. Однако может оказаться необходимым включить в модель качественный фактор, принимающий, два или несколько фиксированных значений-уровней.
Например, можно предположить, что уровень зарплаты в регионе зависит от уровня образования или пола. Или проводя количественный прогноз урожайности включить в уравнение результаты проведенного на предыдущем этапе качественного прогноза (спад, подъем урожая). В моделях связанных с торговлей, маркетингом часто возникает фактор сезонности (зима, весна, лето, осень) при расчете объемов продаж товара. В принципе можно строить отдельные модели для каждого уровня качественного признака, а затем изучать различия между ними. Но есть и другой подход позволяющий использовать одно регрессионное уравнение, но с дополнительными фиктивными (структурными, манекенными (dummy)) переменными.
Часто используют модели с бинарными переменными принимающими два значения 0 и 1. Можно, конечно вводить и переменные принимающие несколько значений, но в этом случае возникают проблемы с интерпретацией коэффициентов модели. Поэтому, если есть переменная, принимающая k значений, то ее заменяют (k – 1 )- й бинарной переменной. Например, если предварительный качественный прогноз урожая может быть сформулирован как 1) спад; 2) практически останется на прежнем уровне; 3) подъем, то в модель вводится две бинарных переменных:
 ,
,
 . (3.42)
. (3.42)
Далее мы строим модель вида
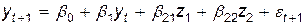 , (3.43)
, (3.43)
где 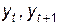 — урожайности сельскохозяйственной культуры в текущем и будущем году.
— урожайности сельскохозяйственной культуры в текущем и будущем году.
Принимая модель (3.43), мы предполагаем, что средняя сила влияния 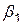 урожая текущего года на урожай будущего года одинакова для всех трех случаев прогноза, а переменные
урожая текущего года на урожай будущего года одинакова для всех трех случаев прогноза, а переменные  отражают особенности агрометеоситуации в неблагоприятные и благоприятные годы для данной сельскохозяйственной культуры.
отражают особенности агрометеоситуации в неблагоприятные и благоприятные годы для данной сельскохозяйственной культуры.
Фиктивные переменные позволяют строить модели для исследования структурных изменений. При этом мы получаем кусочно-линейные модели.
Пусть  зависимая переменная, например, урожайность сельскохозяйственной культуры,
зависимая переменная, например, урожайность сельскохозяйственной культуры, 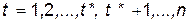 - период наблюдения. Предположим, исследователь считает, что с начала 90-х годов в сельском хозяйстве произошли структурные изменения и линия регрессии будет отличаться от той, что была при
- период наблюдения. Предположим, исследователь считает, что с начала 90-х годов в сельском хозяйстве произошли структурные изменения и линия регрессии будет отличаться от той, что была при 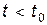 . Чтобы оценить такую модель, введем бинарную переменную
. Чтобы оценить такую модель, введем бинарную переменную 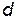 , полагая
, полагая 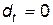 при
при 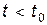 и
и  при
при 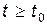 . Пусть
. Пусть 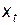 - некоторая объясняющая переменная, например, фондовооруженность отрасли.
- некоторая объясняющая переменная, например, фондовооруженность отрасли.
Запишем следующее регрессионное уравнение
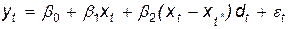 . (3.44)
. (3.44)
Линия регрессии (3.44) имеет коэффициент наклона 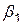 при
при 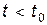 и
и 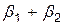 при
при 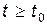 . Отметим, что разрыва при
. Отметим, что разрыва при  не происходит. Оценка значимости коэффициента
не происходит. Оценка значимости коэффициента 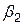 означает проверку гипотезы
означает проверку гипотезы  - структурных изменений в сельском хозяйстве не произошло.
- структурных изменений в сельском хозяйстве не произошло.
Если включать в модель несколько качественных факторов, то надо следить за тем, чтобы включаемые факторы были линейно независимые. Это значит, что в информационной матрице 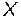 скалярные произведения столбцов, отвечающих за качественные переменные были равны нулю.
скалярные произведения столбцов, отвечающих за качественные переменные были равны нулю.