Изучим возможность прогноза урожая, используя в качестве исходных данных для прогноза результаты оперативного прогноза урожая текущего года по данным хода уборки урожая на примере прогнозирования урожаев зерновых культур в России. Исходные данные о ходе уборки за период с 1992 по 1999 годы были получены в Министерстве сельского хозяйства РФ. Данные наблюдений за ходом уборки даны в табл. 3.10.
Таблица 3.10
Оперативные данные урожайности зерновых культур
в РФ за 1992 - 1999 гг.
| Российская Федерация | |||||||
| 10.авг | 31.авг | 14.сен | 28.сен | 05.окт | 12.окт | ||
| Урожайность, ц/га | 23,8 | 21,7 | 20,6 | 19,9 | 19,7 | ||
| 09.авг | 30.авг | 13.сен | 27.сен | 04.окт | 11.окт | 01.ноя | |
| Урожайность, ц/га | 27,5 | 22,8 | 21,4 | 20,4 | 19,9 | 19,4 | 18,9 |
| 08.авг | 29.авг | 12.сен | 26.сен | 03.окт | 10.окт | 31.окт | |
| Урожайность, ц/га | 23,4 | 20,9 | 19,1 | 17,5 | 17,3 | 17,3 | |
| 07.авг | 28.авг | 11.сен | 25.сен | 02.окт | 09.окт | 30.окт | |
| Урожайность, ц/га | 14,8 | 14,5 | 14,5 | 14,6 | 14,6 | 4,6 | 14,6 |
| 12.авг | 02.сен | 16.сен | 30.сен | 07.окт | 14.окт | 04.ноя | |
| Урожайность, ц/га | 17,5 | 16,7 | 16,6 | 16,5 | 16,4 | 16,3 | 16,4 |
| 11.авг | 01.сен | 15.сен | 29.сен | 06.окт | 13.окт | 03.ноя | |
| Урожайность, ц/га | 22,1 | 20,1 | 19,7 | 19,5 | 19,4 | 19,4 | 19,5 |
| 10.авг | 31.авг | 14.сен | 28.сен | 12.окт | 02.ноя | ||
| Урожайность, ц/га | 16,5 | 14,2 | 13,9 | 14,1 | 14,3 | ||
| 09.авг | 30.авг | 13.сен | 27.сен | 04.окт | 11.окт | 01.ноя | |
| Урожайность, ц/га | 19,4 | 15,7 | 15,1 | 14,9 | 15,2 | 15,3 | 15,2 |
Прогноз знака колебаний урожайности составлялся по методу «Зонт» и проводился на основе данных прошлых лет. Приведем некоторые результаты по построению регрессионных зависимостей для прогноза зерновых в целом по России, табл. 3.11.
Пусть Y1 – данные урожайности зерновых культур в целом на 12 сентября; Y – бункерная урожайность на 14 - 15 октября; Y2 – фиктивная переменная, принимающая значение 1 при прогнозируемом подъеме и значение -1 при прогнозируемом спаде урожайности в текущем году.
Таблица 3.11
Регрессионная модель без учета глобального прогноза для оперативного
прогноза урожайности зерновых в России по данным на 12-14 сентября
| Модель без учета глобального прогноза Y = 5,52 + 0,6267Y1 | |||
| Сумма квадратов, объясняемая уравнением регрессии 32,357 Сумма квадратов остатков 4,092. Общая сумма квадратов 36,45 | |||
| Годы | Исходные данные урожайности | Расчетные значения | Остатки |
| 1992 | 19,7 | 19,12 | 0,57 |
| 1993 | 19,4 | 19,81 | -0,41 |
| 1994 | 17,3 | 18,63 | -1,32 |
| 1995 | 14.6 | 14,62 | -0,02 |
| 1996 | 16,3 | 15,99 | 0,3 |
| 1997 | 19,4 | 18,12 | 1,28 |
| 1998 | 14,1 | 14,43 | -0,32 |
| 1999 | 15,3 | 15,37 | -0,07 |
| Сумма модулей ошибок равна 4,29; Средняя абсолютная ошибка равна 0,53; R2 =0,8877; R=0,9422; F(1,6)=47,446; p < 0,00046; Критерий Стьюдента для свободного члена = 3,27; p = 0,017; Критерий Стьюдента для коэффициента при Y1 = 6,89; p = 0,00046. |
Перейдем к уравнению, использующему глобальный прогноз урожайности зерновых в России, табл. 3.12.
Результаты расчетов по последней модели, по нашему мнению, практически не могут быть улучшены, так как средняя абсолютная ошибка находится в пределах ошибки сбора данных. Уравнение полностью адекватно исходным данным.
Мы рассмотрели модели с фиктивными переменными, в которых фиктивные переменные были объясняющими переменными, то есть факторами. Однако может возникнуть необходимость строить модели, в которых качественный признак играет роль результирующей переменной. Подобные задачи возникают при обработке данных социологических опросов, прогнозировании подъемов и спадов (например, урожайностей сельскохозяйственных культур). Кроме того, если результирующий признак является некоторой вероятностью (например, вероятностью наступления некоторого события), то результирующая переменная должна принимать значения хотя и в непрерывном, но в ограниченном отрезком [0; 1] диапазоне значений.
Таблица 3.12
Регрессионная модель с учетом глобального прогноза для оперативного прогноза урожайности зерновых в России по данным на 12-14 сентября
| Модель с учетом глобального прогноза Y = 5,7374 + 0,6153Y1 + 0,524Y2 | |||
| Сумма квадратов, объясняемая уравнением регрессии = 34,54 Сумма квадратов остатков = 1,9. Общая сумма квадратов = 36,45 | |||
| Годы | Исходные данные урожайности | Расчетные значения | Остатки |
| 1992 | 19,7 | 19,61 | 0,09 |
| 1993 | 19,4 | 19,24 | 0,16 |
| 1994 | 17,3 | 18,07 | - 0,77 |
| 1995 | 14.6 | 14,13 | 0,47 |
| 1996 | 16,3 | 16,53 | - 0,24 |
| 1997 | 19,4 | 18,62 | 0,77 |
| 1998 | 14,1 | 13,95 | 0,15 |
| 1999 | 15,3 | 15,92 | - 0,62 |
| Сумма модулей ошибок равна 3,27; Средняя абсолютная ошибка равна 0,41; R2 =0,948; R=0,973; F(2,5)=45,32; p < 0,00062; Критерий Стьюдента для свободного члена = 4,523; p =0,0063; Критерий Стьюдента для коэффициента при Y1 = 9,024; p = 0,0047 Критерий Стьюдента для коэффициента при Y2 = 2,4; p = 0,062. |
Такие модели часто применимы к социологическим задачам, задачам маркетинга для обработки результатов опросов. Для оценки параметров таких моделей применяются методы логистической регрессии, Logit-, Probit-, Tobit-анализа.
Например, логистическая регрессия — форма регрессии, которая используется, когда зависимая переменная — дихотомия, то есть может принимать только два значения, например, 0 и 1. А независимые переменные могут быть непрерывными или категориальными переменными.
Пусть зависимая переменная принимает значение 1 при появлении некоторого события А, и 0, если событие А не появилось. При каждом наблюдаемом фиксированном наборе факторов вычисляется 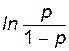 , где
, где 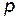 — число появлений единиц, а
— число появлений единиц, а 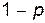 — число появлений нулей в наблюдениях.
— число появлений нулей в наблюдениях.
Логистическая регрессия имеет много аналогий с обычной МНК регрессией, хотя для оценки коэффициентов регрессии используется метод максимального правдоподобия, а не метод наименьших квадратов. В отличие от МНК регрессии, однако, логистическая регрессия оценивает нелинейную связь между независимыми переменными и зависимой, для нее нет проблемы гетероскедастичности, изучаемой ниже, и вообще имеет менее строгие требования. Успех логистической регрессии может быть оценен, по таблице числа правильных и неправильных классификаций дихотомической, зависимой переменной. Для проверки адекватности модели можно использовать критерии согласия, например критерий 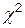 , а проверку значимости коэффициентов можно проводить обычным способом.
, а проверку значимости коэффициентов можно проводить обычным способом.