Докажем несмещенность МНК оценок, используя матричное представление (3.8). В матричном виде уравнение (3.1) записывается в виде:
. (3.9)
Отсюда
. (3.10)
Наконец,
= 
,
что и требовалось.
Рассмотрим матрицу ковариаций оценок bi коэффициентов модели:
.
Для 
получаем равенство:
аналогично имеем: 
. Отсюда
.
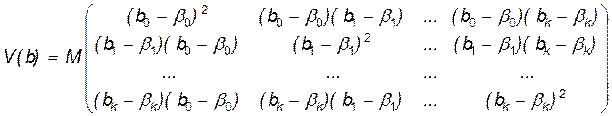В матричной форме последнее равенство записывается в виде:
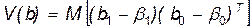. (3.11)
Из (3.8) следует, что
(3.12)
Следовательно,
(3.13)
Отметим, что в (3.13) использовано свойство симметричной матрицы 
не изменяться при транспонировании. Перемножая равенства (3.12) и (3.13) получаем
.
Но из свойств налагаемых на вектор случайных ошибок e вытекает, что
=
= 
= 
=
= 
= 
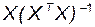. (3.14)
Обозначим элементы матрицы 
за 
. Тогда 
, а 
. Переходя к выборочным оценкам 
получаем, что
, 
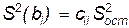. (3.15)
Заметим без доказательства, что оценки bi полученные по МНК оказываются эффективными и состоятельными.
Оценка качества модели
Отклонения 
называют абсолютной ошибкой аппроксимации в i -ом наблюдении, а относительной ошибкой аппроксимации называют величину 
. О качестве модели судят по средней относительной ошибке аппроксимации 
.
Считается, что ошибка в 4 – 9 % на контрольной выборке свидетельствует о хорошем качестве построенной модели. О качестве модели судят также и по результатам дисперсионного анализа модели.
Рассмотрим, как и для случая парной регрессии
(3.16)
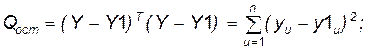(3.17)
(3.18)
Можно показать, что
(3.19)
Докажем это равенство.
Докажем, что две последние суммы равны нулю.
.
Равенство 
эквивалентно равенству 
или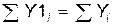 
. Последнее равенство является первым равенством нормальной системы уравнений МНК (с учетом того, что 
, 
Равенство (3.19) доказано.
С вопросом об оценке качества модели тесно связано понятие коэффициента множественной корреляции. В главе 2 рассматривался коэффициент детерминации 
. Он показывает насколько предсказания по уравнению регрессии лучше, чем по среднему значению отклика 
. Число 
называют коэффициентом множественной корреляции. Оказывается, это число совпадает с коэффициентом корреляции между 
и 
, который отражает тесноту линейной связи между значениями выхода и их расчетными значениями . Докажем этот факт. Надо установить равенство
. (3.20)
Для этого достаточно показать, что числитель равен 
, а знаменатель равен 
. Сначала заметим, что в силу ранее доказанного равенства 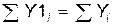получаем 
. Отсюда вытекает требуемое соотношение для знаменателя. Далее,
= 
= 
= 
== + 
.
Выше было показано, что последнее слагаемое равно нулю, что и требовалось.
Дисперсионный анализ для случая многих факторов проводится также как и для парной регрессии. Сделаем только замечания по поводу подсчета степеней свободы для 
и
Обозначим nост = N – k – 1. Это число называется числом степеней свободы остаточной суммы квадратов . Оно равно разности между числом наблюдений и числом линейных связей между ними, участвующими в определении (в сумме участвуют значения 
, которые, в свою очередь, зависят от вектора коэффициентов b = 
).
Несмещенная оценка дисперсии ошибок наблюдений задается в этом случае формулой
.
Аналогично, сумма 
имеет число степеней свободы n общ равное 
, так как в этой сумме все наблюдения связаны одной связью (участвует одно значение ). Наконец, для суммы число степеней свободы
,
так как в выражение входят 
оценок и одна линейная связь, определяемая . Очевидно, что nобщ = nост + nрегр.
Проверка значимости уравнения регрессии проводится по изложенной в предыдущей главе схеме. Находят 
и наблюдаемое значение критерия Фишера 
. Если уравнение регрессии незначимо, то в условиях Гаусса-Маркова числитель и знаменатель дроби являются несмещенными оценками для и дробь подчиняется распределению Фишера-Снедекора. Затем по заданной надежности g = 
, где 
- уровень значимости, по таблицам данного распределения находим критическое значение 
. Если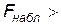 
, то нулевая гипотеза о незначимости уравнения регрессии отвергается и принимается гипотеза о значимости уравнения регрессии.
Формула (3.20) дает выборочное значение коэффициента множественной корреляции, являющейся оценкой фактического его значения 
. Иногда возникает необходимость проверки значимости этого коэффициента, то есть необходимость проверки нулевой гипотезы: = 0 эквивалентной проверке значимости уравнения регрессии. Для проверки этой гипотезы составляют соотношение
= 
.
Далее проверка значимости коэффициента совпадает полностью с проверкой значимости уравнения регрессии.
В случае, когда наблюдения проводились с повторениями, то есть при некотором наборе 
было проведено n дополнительных повторных опытов, появляется возможность проверить качество выбора модели, то есть ее адекватность опытным данным. Пусть в дополнительной точке получены значения 
, которые отражают лишь влияние случайных ошибок или, в худшем случае, влияние неучтенных факторов на результаты наблюдений. Оценим дисперсию ошибок по этим данным
.
Если регрессия адекватна наблюдениям, то и 
и 
будут несмещенными оценками одной и той же дисперсии случайных ошибок .
Итак, нулевая гипотеза в этом случае имеет вид
. (3.21)
А конкурирующая гипотеза утверждает, что равенство (3.21) не выполняется, то есть остатки модели слишком велики по сравнению с ошибками наблюдений и, следовательно, модель (3.1) неадекватна. Это позволяет использовать критерий Фишера для проверки адекватности регрессионной модели. Сначала выберем уровень значимости в пределах от 0,01 до 0,1 и из таблиц распределения Фишера найти величину 
. Затем находят 
. Если 
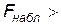
, нет оснований отвергнуть гипотезу об адекватности, если гипотеза об адекватности модели отвергается.